Hipparchus

Hipparchus before-mentioned, who can never be sufficiently praised, no one having done more to prove that man is related to the stars and that our souls are a part of heaven, detected a new star that came into existence during his lifetime; the movement of this star in its line of radiance led him to wonder whether this was a frequent occurrence, whether the stars that we think to be fixed are also in motion; and consequently he did a bold thing, that would be reprehensible even for God - he dared to schedule the stars for posterity, and tick off the heavenly bodies by name in a list, devising machinery by means of which to indicate their several positions and magnitudes, in order that from that time onward it might be possible easily to discern not only whether stars perish and are born, but whether some are in transit and in motion, and also whether they increase and decrease in magnitude - thus bequeathing the heavens as a legacy to all mankind, supposing anybody had been found to claim that inheritance! Pliny, Natural History, Book 2) 77 AD on Hipparchus

Hipparchus of Nicaea (/hɪˈpɑːrkəs/; Greek: Ἵππαρχος, Hipparkhos; c. 190 – c. 120 BC) was a Greek astronomer, geographer, and mathematician. He is considered the founder of trigonometry[1] but is most famous for his incidental discovery of precession of the equinoxes.[2]

Hipparchus was born in Nicaea, Bithynia (now İznik, Turkey), and probably died on the island of Rhodes, Greece. He is known to have been a working astronomer at least from 162 to 127 BC.[3] Hipparchus is considered the greatest ancient astronomical observer and, by some, the greatest overall astronomer of antiquity. He was the first whose quantitative and accurate models for the motion of the Sun and Moon survive. For this he certainly made use of the observations and perhaps the mathematical techniques accumulated over centuries by the Babylonians and by Meton of Athens (5th century BC), Timocharis, Aristyllus, Aristarchus of Samos and Eratosthenes, among others.[4] He developed trigonometry and constructed trigonometric tables, and he solved several problems of spherical trigonometry. With his solar and lunar theories and his trigonometry, he may have been the first to develop a reliable method to predict solar eclipses. His other reputed achievements include the discovery and measurement of Earth's precession, the compilation of the first comprehensive star catalog of the western world, and possibly the invention of the astrolabe, also of the armillary sphere, which he used during the creation of much of the star catalogue.

Life and work
Illustrated depiction of Hipparchus observing the sky from Alexandria, 1876

Hipparchus was born in Nicaea (Greek Νίκαια), in the ancient district of Bithynia (modern-day Iznik in province Bursa), in what today is the country Turkey. The exact dates of his life are not known, but Ptolemy attributes astronomical observations to him in the period from 147–127 BC, and some of these are stated as made in Rhodes; earlier observations since 162 BC might also have been made by him. His birth date (c. 190 BC) was calculated by Delambre based on clues in his work. Hipparchus must have lived some time after 127 BC because he analyzed and published his observations from that year. Hipparchus obtained information from Alexandria as well as Babylon, but it is not known when or if he visited these places. He is believed to have died on the island of Rhodes, where he seems to have spent most of his later life.

It is not known what Hipparchus's economic means were nor how he supported his scientific activities. His appearance is likewise unknown: there are no contemporary portraits. In the 2nd and 3rd centuries coins were made in his honour in Bithynia that bear his name and show him with a globe; this supports the tradition that he was born there.

Relatively little of Hipparchus's direct work survives into modern times. Although he wrote at least fourteen books, only his commentary on the popular astronomical poem by Aratus was preserved by later copyists. Most of what is known about Hipparchus comes from Strabo's Geography and Pliny's Natural History in the 1st century; Ptolemy's 2nd-century Almagest; and additional references to him in the 4th century by Pappus and Theon of Alexandria in their commentaries on the Almagest.[5]

Hipparchus was amongst the first to calculate a heliocentric system,[6] but he abandoned his work because the calculations showed the orbits were not perfectly circular as believed to be mandatory by the science of the time. Although a contemporary of Hipparchus', Seleucus of Seleucia, remained a proponent of the heliocentric model, Hipparchus' rejection of heliocentrism, supported by ideas from Aristotle, remained dominant for nearly 2000 years until Copernican heliocentrism turned the tide of the debate.

Hipparchus's only preserved work is Τῶν Ἀράτου καὶ Εὐδόξου φαινομένων ἐξήγησις ("Commentary on the Phaenomena of Eudoxus and Aratus"). This is a highly critical commentary in the form of two books on a popular poem by Aratus based on the work by Eudoxus.[7] Hipparchus also made a list of his major works, which apparently mentioned about fourteen books, but which is only known from references by later authors. His famous star catalog was incorporated into the one by Ptolemy, and may be almost perfectly reconstructed by subtraction of two and two-thirds degrees from the longitudes of Ptolemy's stars. The first trigonometric table was apparently compiled by Hipparchus, who is consequently now known as "the father of trigonometry".

Modern speculation

Hipparchus was in the international news in 2005, when it was again proposed (as in 1898) that the data on the celestial globe of Hipparchus or in his star catalog may have been preserved in the only surviving large ancient celestial globe which depicts the constellations with moderate accuracy, the globe carried by the Farnese Atlas. There are a variety of mis-steps[8] in the more ambitious 2005 paper, thus no specialists in the area accept its widely publicized speculation.[9]

Lucio Russo has said that Plutarch, in his work On the Face in the Moon, was reporting some physical theories that we consider to be Newtonian and that these may have come originally from Hipparchus;[10] he goes on to say that Newton may have been influenced by them.[11] According to one book review, both of these claims have been rejected by other scholars.[12]

A line in Plutarch's Table Talk states that Hipparchus counted 103,049 compound propositions that can be formed from ten simple propositions. 103,049 is the tenth Schröder–Hipparchus number, which counts the number of ways of adding one or more pairs of parentheses around consecutive subsequences of two or more items in any sequence of ten symbols. This has led to speculation that Hipparchus knew about enumerative combinatorics, a field of mathematics that developed independently in modern mathematics.[13][14]

Babylonian sources
Further information: Babylonian astronomy

Earlier Greek astronomers and mathematicians were influenced by Babylonian astronomy to some extent, for instance the period relations of the Metonic cycle and Saros cycle may have come from Babylonian sources (see "Babylonian astronomical diaries"). Hipparchus seems to have been the first to exploit Babylonian astronomical knowledge and techniques systematically.[15] Except for Timocharis and Aristillus, he was the first Greek known to divide the circle in 360 degrees of 60 arc minutes (Eratosthenes before him used a simpler sexagesimal system dividing a circle into 60 parts); he also adopted the Babylonian astronomical cubit unit (Akkadian ammatu, Greek πῆχυς pēchys) which was equivalent to 2° or 2.5° ('large cubit').

Hipparchus probably compiled a list of Babylonian astronomical observations; G. J. Toomer, a historian of astronomy, has suggested that Ptolemy's knowledge of eclipse records and other Babylonian observations in the Almagest came from a list made by Hipparchus. Hipparchus's use of Babylonian sources has always been known in a general way, because of Ptolemy's statements. However, Franz Xaver Kugler demonstrated that the synodic and anomalistic periods that Ptolemy attributes to Hipparchus had already been used in Babylonian ephemerides, specifically the collection of texts nowadays called "System B" (sometimes attributed to Kidinnu).[16]

Hipparchus's long draconitic lunar period (5,458 months = 5,923 lunar nodal periods) also appears a few times in Babylonian records.[17] But the only such tablet explicitly dated is post-Hipparchus so the direction of transmission is not settled by the tablets.

Hipparchus's draconitic lunar motion cannot be solved by the lunar-four arguments that are sometimes proposed to explain his anomalistic motion. A solution that has produced the exact ​5,458⁄5,923 ratio is rejected by most historians though it uses the only anciently attested method of determining such ratios, and it automatically delivers the ratio's four-digit numerator and denominator. Hipparchus initially used (Almagest 6.9) his 141 BC eclipse with a Babylonian eclipse of 720 BC to find the less accurate ratio 7,160 synodic months = 7,770 draconitic months, simplified by him to 716 = 777 through division by 10. (He similarly found from the 345-year cycle the ratio 4267 synodic months = 4573 anomalistic months and divided by 17 to obtain the standard ratio 251 synodic months = 269 anomalistic months.) If he sought a longer time base for this draconitic investigation he could use his same 141 BC eclipse with a moonrise 1245 BC eclipse from Babylon, an interval of 13,645 synodic months = ​14,8807 1⁄2 draconitic months ≈ ​14,623 1⁄2 anomalistic months. Dividing by ​5⁄2 produces 5458 synodic months = 5923 precisely.[18] The obvious main objection is that the early eclipse is unattested though that is not surprising in itself and there is no consensus on whether Babylonian observations were recorded this remotely. Though Hipparchus's tables formally went back only to 747 BC, 600 years before his era, the tables were actually good back to before the eclipse in question because as only recently noted[19] their use in reverse is no more difficult than forwards.

Geometry, trigonometry, and other mathematical techniques

Hipparchus was recognized as the first mathematician known to have possessed a trigonometric table, which he needed when computing the eccentricity of the orbits of the Moon and Sun. He tabulated values for the chord function, which for a central angle in a circle gives the length of the straight line segment between the points where the angle intersects the circle. He computed this for a circle with a circumference of 21,600 units and a radius (rounded) of 3438 units; this circle has a unit length of 1 arc minute along its perimeter. He tabulated the chords for angles with increments of 7.5°. In modern terms, the chord subtended by a central angle in a circle of given radius equals the radius times twice the sine of half of the angle, i.e.:

chord ⁡ ( θ ) = 2 r ⋅ sin ⁡ ( θ 2 ) {\displaystyle \operatorname {chord} (\theta )=2r\cdot \sin \left({\frac {\theta }{2}}\right)} {\displaystyle \operatorname {chord} (\theta )=2r\cdot \sin \left({\frac {\theta }{2}}\right)}

The now lost work in which Hipparchus is said to have developed his chord table, is called Tōn en kuklōi eutheiōn (Of Lines Inside a Circle) in Theon of Alexandria's 4th-century commentary on section I.10 of the Almagest. Some claim the table of Hipparchus may have survived in astronomical treatises in India, like the Surya Siddhanta. Trigonometry was a significant innovation, because it allowed Greek astronomers to solve any triangle, and made it possible to make quantitative astronomical models and predictions using their preferred geometric techniques.[20]

Hipparchus must have used a better approximation for π than the one from Archimedes of between ​3 10⁄71 (3.14085) and ​3 1⁄7 (3.14286). Perhaps he had the one later used by Ptolemy: 3;8,30 (sexagesimal)(3.1417) (Almagest VI.7), but it is not known whether he computed an improved value himself.

Some scholars do not believe Āryabhaṭa's sine table has anything to do with Hipparchus's chord table. Others do not agree that Hipparchus even constructed a chord table. Bo C. Klintberg states, "With mathematical reconstructions and philosophical arguments I show that Toomer's 1973 paper never contained any conclusive evidence for his claims that Hipparchus had a 3438'-based chord table, and that the Indians used that table to compute their sine tables. Recalculating Toomer's reconstructions with a 3600' radius – i.e. the radius of the chord table in Ptolemy's Almagest, expressed in 'minutes' instead of 'degrees' – generates Hipparchan-like ratios similar to those produced by a 3438′ radius. It is therefore possible that the radius of Hipparchus's chord table was 3600′, and that the Indians independently constructed their 3438′-based sine table."[21]

Hipparchus could have constructed his chord table using the Pythagorean theorem and a theorem known to Archimedes. He also might have developed and used the theorem called Ptolemy's theorem; this was proved by Ptolemy in his Almagest (I.10) (and later extended by Carnot).

Hipparchus was the first to show that the stereographic projection is conformal, and that it transforms circles on the sphere that do not pass through the center of projection to circles on the plane. This was the basis for the astrolabe.

Besides geometry, Hipparchus also used arithmetic techniques developed by the Chaldeans. He was one of the first Greek mathematicians to do this, and in this way expanded the techniques available to astronomers and geographers.

There are several indications that Hipparchus knew spherical trigonometry, but the first surviving text discussing it is by Menelaus of Alexandria in the 1st century, who on that basis is now commonly credited with its discovery. (Previous to the finding of the proofs of Menelaus a century ago, Ptolemy was credited with the invention of spherical trigonometry.) Ptolemy later used spherical trigonometry to compute things like the rising and setting points of the ecliptic, or to take account of the lunar parallax. If he did not use spherical trigonometry, Hipparchus may have used a globe for these tasks, reading values off coordinate grids drawn on it, or he may have made approximations from planar geometry, or perhaps used arithmetical approximations developed by the Chaldeans.

Aubrey Diller has shown that the clima calculations which Strabo preserved from Hipparchus could have been performed by spherical trigonometry using the only accurate obliquity known to have been used by ancient astronomers, 23°40′. All thirteen clima figures agree with Diller's proposal.[22] Further confirming his contention is the finding that the big errors in Hipparchus's longitude of Regulus and both longitudes of Spica agree to a few minutes in all three instances with a theory that he took the wrong sign for his correction for parallax when using eclipses for determining stars' positions.[23]
Lunar and solar theory
Geometric construction used by Hipparchus in his determination of the distances to the Sun and Moon.
Motion of the Moon
Further information: Lunar theory and Orbit of the Moon

Hipparchus also studied the motion of the Moon and confirmed the accurate values for two periods of its motion that Chaldean astronomers are widely presumed[24] to have possessed before him, whatever their ultimate origin. The traditional value (from Babylonian System B) for the mean synodic month is 29 days; 31,50,8,20 (sexagesimal) = 29.5305941... days. Expressed as 29 days + 12 hours + 793/1080 hours this value has been used later in the Hebrew calendar. The Chaldeans also knew that 251 synodic months ≈ 269 anomalistic months. Hipparchus used the multiple of this period by a factor of 17, because that interval is also an eclipse period, and is also close to an integer number of years (4267 moons : 4573 anomalistic periods : 4630.53 nodal periods : 4611.98 lunar orbits : 344.996 years : 344.982 solar orbits : 126,007.003 days : 126,351.985 rotations).[note 1] What was so exceptional and useful about the cycle was that all 345-year-interval eclipse pairs occur slightly over 126,007 days apart within a tight range of only about ±​1⁄2 hour, guaranteeing (after division by 4267) an estimate of the synodic month correct to one part in order of magnitude 10 million. The 345-year periodicity is why[25] the ancients could conceive of a mean month and quantify it so accurately that it is even today correct to a fraction of a second of time.

Hipparchus could confirm his computations by comparing eclipses from his own time (presumably 27 January 141 BC and 26 November 139 BC according to [Toomer 1980]), with eclipses from Babylonian records 345 years earlier (Almagest IV.2; [A.Jones, 2001]). Already al-Biruni (Qanun VII.2.II) and Copernicus (de revolutionibus IV.4) noted that the period of 4,267 moons is actually about 5 minutes longer than the value for the eclipse period that Ptolemy attributes to Hipparchus. However, the timing methods of the Babylonians had an error of no less than 8 minutes.[26] Modern scholars agree that Hipparchus rounded the eclipse period to the nearest hour, and used it to confirm the validity of the traditional values, rather than try to derive an improved value from his own observations. From modern ephemerides[27] and taking account of the change in the length of the day (see ΔT) we estimate that the error in the assumed length of the synodic month was less than 0.2 seconds in the 4th century BC and less than 0.1 seconds in Hipparchus's time.
Orbit of the Moon

It had been known for a long time that the motion of the Moon is not uniform: its speed varies. This is called its anomaly, and it repeats with its own period; the anomalistic month. The Chaldeans took account of this arithmetically, and used a table giving the daily motion of the Moon according to the date within a long period. The Greeks however preferred to think in geometrical models of the sky. Apollonius of Perga had at the end of the 3rd century BC proposed two models for lunar and planetary motion:

In the first, the Moon would move uniformly along a circle, but the Earth would be eccentric, i.e., at some distance of the center of the circle. So the apparent angular speed of the Moon (and its distance) would vary.
The Moon itself would move uniformly (with some mean motion in anomaly) on a secondary circular orbit, called an epicycle, that itself would move uniformly (with some mean motion in longitude) over the main circular orbit around the Earth, called deferent; see deferent and epicycle. Apollonius demonstrated that these two models were in fact mathematically equivalent. However, all this was theory and had not been put to practice. Hipparchus was the first astronomer we know attempted to determine the relative proportions and actual sizes of these orbits.

Hipparchus devised a geometrical method to find the parameters from three positions of the Moon, at particular phases of its anomaly. In fact, he did this separately for the eccentric and the epicycle model. Ptolemy describes the details in the Almagest IV.11. Hipparchus used two sets of three lunar eclipse observations, which he carefully selected to satisfy the requirements. The eccentric model he fitted to these eclipses from his Babylonian eclipse list: 22/23 December 383 BC, 18/19 June 382 BC, and 12/13 December 382 BC. The epicycle model he fitted to lunar eclipse observations made in Alexandria at 22 September 201 BC, 19 March 200 BC, and 11 September 200 BC.

For the eccentric model, Hipparchus found for the ratio between the radius of the eccenter and the distance between the center of the eccenter and the center of the ecliptic (i.e., the observer on Earth): 3144 : ​327 2⁄3 ;
and for the epicycle model, the ratio between the radius of the deferent and the epicycle: ​3122 1⁄2 : ​247 1⁄2 .

The somewhat weird numbers are due to the cumbersome unit he used in his chord table according to one group of historians, who explain their reconstruction's inability to agree with these four numbers as partly due to some sloppy rounding and calculation errors by Hipparchus, for which Ptolemy criticised him (he himself made rounding errors too). A simpler alternate reconstruction[28] agrees with all four numbers. Anyway, Hipparchus found inconsistent results; he later used the ratio of the epicycle model (​3122 1⁄2 : ​247 1⁄2), which is too small (60 : 4;45 sexagesimal). Ptolemy established a ratio of 60 : ​5 1⁄4.[29] (The maximum angular deviation producible by this geometry is the arcsin of ​5 1⁄4 divided by 60, or about 5° 1', a figure that is sometimes therefore quoted as the equivalent of the Moon's equation of the center in the Hipparchan model.)
Apparent motion of the Sun

Before Hipparchus, Meton, Euctemon, and their pupils at Athens had made a solstice observation (i.e., timed the moment of the summer solstice) on 27 June 432 BC (proleptic Julian calendar). Aristarchus of Samos is said to have done so in 280 BC, and Hipparchus also had an observation by Archimedes. As shown in a 1991 paper, in 158 BC Hipparchus computed a very erroneous summer solstice from Callippus's calendar. He observed the summer solstice in 146 and 135 BC both accurate to a few hours, but observations of the moment of equinox were simpler, and he made twenty during his lifetime. Ptolemy gives an extensive discussion of Hipparchus's work on the length of the year in the Almagest III.1, and quotes many observations that Hipparchus made or used, spanning 162–128 BC. Analysis of Hipparchus's seventeen equinox observations made at Rhodes shows that the mean error in declination is positive seven arc minutes, nearly agreeing with the sum of refraction by air and Swerdlow's parallax. The random noise is two arc minutes or more nearly one arcminute if rounding is taken into account which approximately agrees with the sharpness of the eye. Ptolemy quotes an equinox timing by Hipparchus (at 24 March 146 BC at dawn) that differs by 5 hours from the observation made on Alexandria's large public equatorial ring that same day (at 1 hour before noon): Hipparchus may have visited Alexandria but he did not make his equinox observations there; presumably he was on Rhodes (at nearly the same geographical longitude). He could have used the equatorial ring of his armillary sphere or another equatorial ring for these observations, but Hipparchus (and Ptolemy) knew that observations with these instruments are sensitive to a precise alignment with the equator, so if he were restricted to an armillary, it would make more sense to use its meridian ring as a transit instrument. The problem with an equatorial ring (if an observer is naive enough to trust it very near dawn or dusk) is that atmospheric refraction lifts the Sun significantly above the horizon: so for a northern hemisphere observer its apparent declination is too high, which changes the observed time when the Sun crosses the equator. (Worse, the refraction decreases as the Sun rises and increases as it sets, so it may appear to move in the wrong direction with respect to the equator in the course of the day – as Ptolemy mentions. Ptolemy and Hipparchus apparently did not realize that refraction is the cause.) However, such details have doubtful relation to the data of either man, since there is no textual, scientific, or statistical ground for believing that their equinoxes were taken on an equatorial ring, which is useless for solstices in any case. Not one of two centuries of mathematical investigations of their solar errors has claimed to have traced them to the effect of refraction on use of an equatorial ring. Ptolemy claims his solar observations were on a transit instrument set in the meridian.

Recent expert translation and analysis by Anne Tihon of papyrus P. Fouad 267 A has confirmed the 1991 finding cited above that Hipparchus obtained a summer solstice in 158 BC But the papyrus makes the date 26 June, over a day earlier than the 1991 paper's conclusion for 28 June. The earlier study's §M found that Hipparchus did not adopt 26 June solstices until 146 BC when he founded the orbit of the Sun which Ptolemy later adopted. Dovetailing these data suggests Hipparchus extrapolated the 158 BC 26 June solstice from his 145 solstice 12 years later a procedure that would cause only minuscule error. The papyrus also confirmed that Hipparchus had used Callippic solar motion in 158 BC, a new finding in 1991 but not attested directly until P. Fouad 267 A. Another table on the papyrus is perhaps for sidereal motion and a third table is for Metonic tropical motion, using a previously unknown year of ​365 1⁄4 – ​1⁄309 days. This was presumably found[30] by dividing the 274 years from 432 to 158 BC, into the corresponding interval of 100077 days and ​14 3⁄4 hours between Meton's sunrise and Hipparchus's sunset solstices.

At the end of his career, Hipparchus wrote a book called Peri eniausíou megéthous ("On the Length of the Year") about his results. The established value for the tropical year, introduced by Callippus in or before 330 BC was ​365 1⁄4 days.[31] Speculating a Babylonian origin for the Callippic year is hard to defend, since Babylon did not observe solstices thus the only extant System B year length was based on Greek solstices (see below). Hipparchus's equinox observations gave varying results, but he himself points out (quoted in Almagest III.1(H195)) that the observation errors by himself and his predecessors may have been as large as ​1⁄4 day. He used old solstice observations, and determined a difference of about one day in about 300 years. So he set the length of the tropical year to ​365 1⁄4 − ​1⁄300 days (= 365.24666... days = 365 days 5 hours 55 min, which differs from the actual value (modern estimate, including earth spin acceleration) in his time of about 365.2425 days, an error of about 6 min per year, an hour per decade, 10 hours per century.

Between the solstice observation of Meton and his own, there were 297 years spanning 108,478 days. D. Rawlins noted that this implies a tropical year of 365.24579... days = 365 days;14,44,51 (sexagesimal; = 365 days + 14/60 + 44/602 + 51/603) and that this exact year length has been found on one of the few Babylonian clay tablets which explicitly specifies the System B month. This is an indication that Hipparchus's work was known to Chaldeans.[32]

Another value for the year that is attributed to Hipparchus (by the astrologer Vettius Valens in the 1st century) is 365 + 1/4 + 1/288 days (= 365.25347... days = 365 days 6 hours 5 min), but this may be a corruption of another value attributed to a Babylonian source: 365 + 1/4 + 1/144 days (= 365.25694... days = 365 days 6 hours 10 min). It is not clear if this would be a value for the sidereal year (actual value at his time (modern estimate) about 365.2565 days), but the difference with Hipparchus's value for the tropical year is consistent with his rate of precession (see below).
Orbit of the Sun

Before Hipparchus, astronomers knew that the lengths of the seasons are not equal. Hipparchus made observations of equinox and solstice, and according to Ptolemy (Almagest III.4) determined that spring (from spring equinox to summer solstice) lasted 94½ days, and summer (from summer solstice to autumn equinox) ​92 1⁄2 days. This is inconsistent with a premise of the Sun moving around the Earth in a circle at uniform speed. Hipparchus's solution was to place the Earth not at the center of the Sun's motion, but at some distance from the center. This model described the apparent motion of the Sun fairly well. It is known today that the planets, including the Earth, move in approximate ellipses around the Sun, but this was not discovered until Johannes Kepler published his first two laws of planetary motion in 1609. The value for the eccentricity attributed to Hipparchus by Ptolemy is that the offset is ​1⁄24 of the radius of the orbit (which is a little too large), and the direction of the apogee would be at longitude 65.5° from the vernal equinox. Hipparchus may also have used other sets of observations, which would lead to different values. One of his two eclipse trios' solar longitudes are consistent with his having initially adopted inaccurate lengths for spring and summer of ​95 3⁄4 and ​91 1⁄4 days.[33] His other triplet of solar positions is consistent with ​94 1⁄4 and ​92 1⁄2 days,[34] an improvement on the results (​94 1⁄2 and ​92 1⁄2 days) attributed to Hipparchus by Ptolemy, which a few scholars still question the authorship of. Ptolemy made no change three centuries later, and expressed lengths for the autumn and winter seasons which were already implicit (as shown, e.g., by A. Aaboe).
Distance, parallax, size of the Moon and the Sun
Main article: Hipparchus on sizes and distances
Diagram used in reconstructing one of Hipparchus's methods of determining the distance to the Moon. This represents the Earth–Moon system during a partial solar eclipse at A (Alexandria) and a total solar eclipse at H (Hellespont).

Hipparchus also undertook to find the distances and sizes of the Sun and the Moon. His results appear in two works: Perí megethōn kaí apostēmátōn ("On Sizes and Distances") by Pappus and in Pappus's commentary on the Almagest V.11; Theon of Smyrna (2nd century) mentions the work with the addition "of the Sun and Moon".

Hipparchus measured the apparent diameters of the Sun and Moon with his diopter. Like others before and after him, he found that the Moon's size varies as it moves on its (eccentric) orbit, but he found no perceptible variation in the apparent diameter of the Sun. He found that at the mean distance of the Moon, the Sun and Moon had the same apparent diameter; at that distance, the Moon's diameter fits 650 times into the circle, i.e., the mean apparent diameters are ​360⁄650 = 0°33′14″.

Like others before and after him, he also noticed that the Moon has a noticeable parallax, i.e., that it appears displaced from its calculated position (compared to the Sun or stars), and the difference is greater when closer to the horizon. He knew that this is because in the then-current models the Moon circles the center of the Earth, but the observer is at the surface—the Moon, Earth and observer form a triangle with a sharp angle that changes all the time. From the size of this parallax, the distance of the Moon as measured in Earth radii can be determined. For the Sun however, there was no observable parallax (we now know that it is about 8.8", several times smaller than the resolution of the unaided eye).

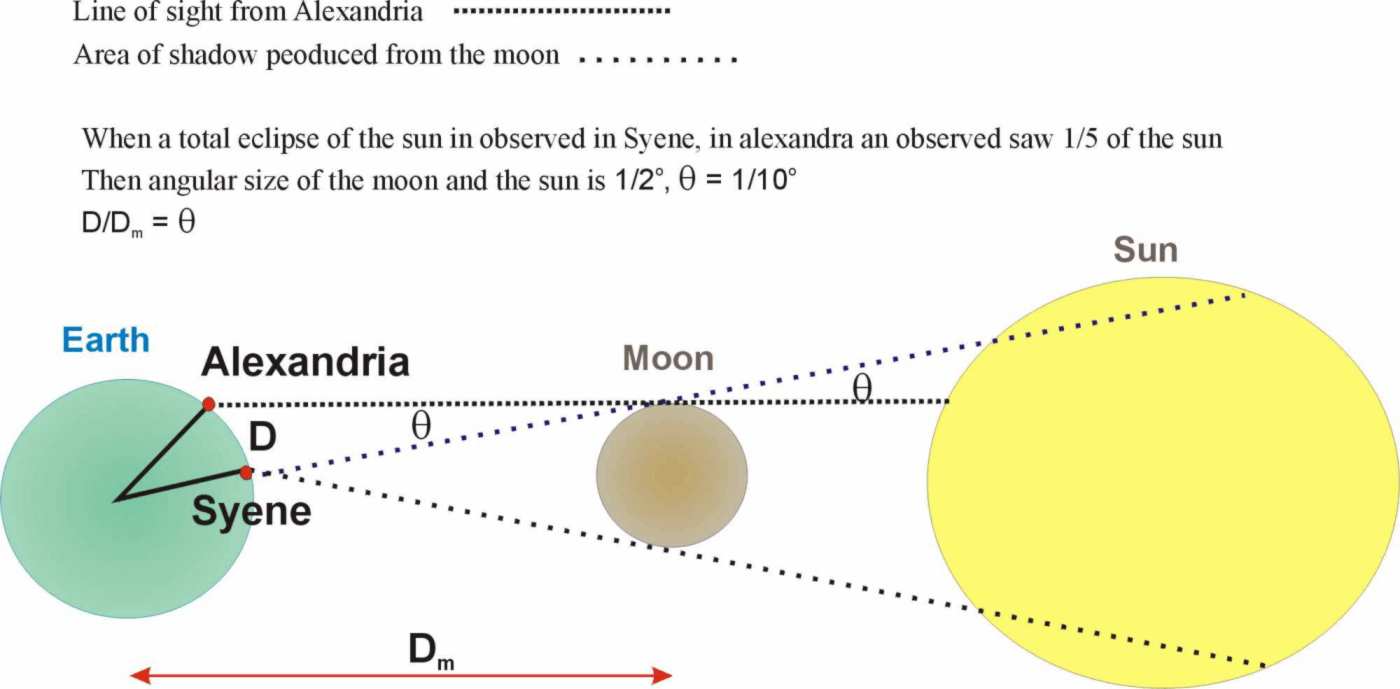
In the first book, Hipparchus assumes that the parallax of the Sun is 0, as if it is at infinite distance. He then analyzed a solar eclipse, which Toomer (against the opinion of over a century of astronomers) presumes to be the eclipse of 14 March 190 BC.[35] It was total in the region of the Hellespont (and in his birthplace, Nicaea); at the time Toomer proposes the Romans were preparing for war with Antiochus III in the area, and the eclipse is mentioned by Livy in his Ab Urbe Condita Libri VIII.2. It was also observed in Alexandria, where the Sun was reported to be obscured 4/5ths by the Moon. Alexandria and Nicaea are on the same meridian. Alexandria is at about 31° North, and the region of the Hellespont about 40° North. (It has been contended that authors like Strabo and Ptolemy had fairly decent values for these geographical positions, so Hipparchus must have known them too. However, Strabo's Hipparchus dependent latitudes for this region are at least 1° too high, and Ptolemy appears to copy them, placing Byzantium 2° high in latitude.) Hipparchus could draw a triangle formed by the two places and the Moon, and from simple geometry was able to establish a distance of the Moon, expressed in Earth radii. Because the eclipse occurred in the morning, the Moon was not in the meridian, and it has been proposed that as a consequence the distance found by Hipparchus was a lower limit. In any case, according to Pappus, Hipparchus found that the least distance is 71 (from this eclipse), and the greatest 81 Earth radii.

In the second book, Hipparchus starts from the opposite extreme assumption: he assigns a (minimum) distance to the Sun of 490 Earth radii. This would correspond to a parallax of 7′, which is apparently the greatest parallax that Hipparchus thought would not be noticed (for comparison: the typical resolution of the human eye is about 2′; Tycho Brahe made naked eye observation with an accuracy down to 1′). In this case, the shadow of the Earth is a cone rather than a cylinder as under the first assumption. Hipparchus observed (at lunar eclipses) that at the mean distance of the Moon, the diameter of the shadow cone is ​2 1⁄2 lunar diameters. That apparent diameter is, as he had observed, ​360⁄650 degrees. With these values and simple geometry, Hipparchus could determine the mean distance; because it was computed for a minimum distance of the Sun, it is the maximum mean distance possible for the Moon. With his value for the eccentricity of the orbit, he could compute the least and greatest distances of the Moon too. According to Pappus, he found a least distance of 62, a mean of ​67 1⁄3, and consequently a greatest distance of ​72 2⁄3 Earth radii. With this method, as the parallax of the Sun decreases (i.e., its distance increases), the minimum limit for the mean distance is 59 Earth radii – exactly the mean distance that Ptolemy later derived.

Hipparchus thus had the problematic result that his minimum distance (from book 1) was greater than his maximum mean distance (from book 2). He was intellectually honest about this discrepancy, and probably realized that especially the first method is very sensitive to the accuracy of the observations and parameters. (In fact, modern calculations show that the size of the 189 BC solar eclipse at Alexandria must have been closer to ​9⁄10ths and not the reported ​4⁄5ths, a fraction more closely matched by the degree of totality at Alexandria of eclipses occurring in 310 and 129 BC which were also nearly total in the Hellespont and are thought by many to be more likely possibilities for the eclipse Hipparchus used for his computations.)

Ptolemy later measured the lunar parallax directly (Almagest V.13), and used the second method of Hipparchus with lunar eclipses to compute the distance of the Sun (Almagest V.15). He criticizes Hipparchus for making contradictory assumptions, and obtaining conflicting results (Almagest V.11): but apparently he failed to understand Hipparchus's strategy to establish limits consistent with the observations, rather than a single value for the distance. His results were the best so far: the actual mean distance of the Moon is 60.3 Earth radii, within his limits from Hipparchus's second book.

Theon of Smyrna wrote that according to Hipparchus, the Sun is 1,880 times the size of the Earth, and the Earth twenty-seven times the size of the Moon; apparently this refers to volumes, not diameters. From the geometry of book 2 it follows that the Sun is at 2,550 Earth radii, and the mean distance of the Moon is ​60 1⁄2 radii. Similarly, Cleomedes quotes Hipparchus for the sizes of the Sun and Earth as 1050:1; this leads to a mean lunar distance of 61 radii. Apparently Hipparchus later refined his computations, and derived accurate single values that he could use for predictions of solar eclipses.

See [Toomer 1974] for a more detailed discussion.
Eclipses

Pliny (Naturalis Historia II.X) tells us that Hipparchus demonstrated that lunar eclipses can occur five months apart, and solar eclipses seven months (instead of the usual six months); and the Sun can be hidden twice in thirty days, but as seen by different nations. Ptolemy discussed this a century later at length in Almagest VI.6. The geometry, and the limits of the positions of Sun and Moon when a solar or lunar eclipse is possible, are explained in Almagest VI.5. Hipparchus apparently made similar calculations. The result that two solar eclipses can occur one month apart is important, because this can not be based on observations: one is visible on the northern and the other on the southern hemisphere – as Pliny indicates – and the latter was inaccessible to the Greek.

Prediction of a solar eclipse, i.e., exactly when and where it will be visible, requires a solid lunar theory and proper treatment of the lunar parallax. Hipparchus must have been the first to be able to do this. A rigorous treatment requires spherical trigonometry, thus those who remain certain that Hipparchus lacked it must speculate that he may have made do with planar approximations. He may have discussed these things in Perí tēs katá plátos mēniaías tēs selēnēs kinēseōs ("On the monthly motion of the Moon in latitude"), a work mentioned in the Suda.

Pliny also remarks that "he also discovered for what exact reason, although the shadow causing the eclipse must from sunrise onward be below the earth, it happened once in the past that the Moon was eclipsed in the west while both luminaries were visible above the earth" (translation H. Rackham (1938), Loeb Classical Library 330 p. 207). Toomer (1980) argued that this must refer to the large total lunar eclipse of 26 November 139 BC, when over a clean sea horizon as seen from Rhodes, the Moon was eclipsed in the northwest just after the Sun rose in the southeast. This would be the second eclipse of the 345-year interval that Hipparchus used to verify the traditional Babylonian periods: this puts a late date to the development of Hipparchus's lunar theory. We do not know what "exact reason" Hipparchus found for seeing the Moon eclipsed while apparently it was not in exact opposition to the Sun. Parallax lowers the altitude of the luminaries; refraction raises them, and from a high point of view the horizon is lowered.
Astronomical instruments and astrometry

Hipparchus and his predecessors used various instruments for astronomical calculations and observations, such as the gnomon, the astrolabe, and the armillary sphere.

Hipparchus is credited with the invention or improvement of several astronomical instruments, which were used for a long time for naked-eye observations. According to Synesius of Ptolemais (4th century) he made the first astrolabion: this may have been an armillary sphere (which Ptolemy however says he constructed, in Almagest V.1); or the predecessor of the planar instrument called astrolabe (also mentioned by Theon of Alexandria). With an astrolabe Hipparchus was the first to be able to measure the geographical latitude and time by observing fixed stars. Previously this was done at daytime by measuring the shadow cast by a gnomon, by recording the length of the longest day of the year or with the portable instrument known as a scaphe.
Equatorial ring of Hipparchus's time.

Ptolemy mentions (Almagest V.14) that he used a similar instrument as Hipparchus, called dioptra, to measure the apparent diameter of the Sun and Moon. Pappus of Alexandria described it (in his commentary on the Almagest of that chapter), as did Proclus (Hypotyposis IV). It was a 4-foot rod with a scale, a sighting hole at one end, and a wedge that could be moved along the rod to exactly obscure the disk of Sun or Moon.

Hipparchus also observed solar equinoxes, which may be done with an equatorial ring: its shadow falls on itself when the Sun is on the equator (i.e., in one of the equinoctial points on the ecliptic), but the shadow falls above or below the opposite side of the ring when the Sun is south or north of the equator. Ptolemy quotes (in Almagest III.1 (H195)) a description by Hipparchus of an equatorial ring in Alexandria; a little further he describes two such instruments present in Alexandria in his own time.

Hipparchus applied his knowledge of spherical angles to the problem of denoting locations on the Earth's surface. Before him a grid system had been used by Dicaearchus of Messana, but Hipparchus was the first to apply mathematical rigor to the determination of the latitude and longitude of places on the Earth. Hipparchus wrote a critique in three books on the work of the geographer Eratosthenes of Cyrene (3rd century BC), called Pròs tèn Eratosthénous geographían ("Against the Geography of Eratosthenes"). It is known to us from Strabo of Amaseia, who in his turn criticised Hipparchus in his own Geographia. Hipparchus apparently made many detailed corrections to the locations and distances mentioned by Eratosthenes. It seems he did not introduce many improvements in methods, but he did propose a means to determine the geographical longitudes of different cities at lunar eclipses (Strabo Geographia 1 January 2012). A lunar eclipse is visible simultaneously on half of the Earth, and the difference in longitude between places can be computed from the difference in local time when the eclipse is observed. His approach would give accurate results if it were correctly carried out but the limitations of timekeeping accuracy in his era made this method impractical.
Star catalog
Hipparchus holding his celestial globe, in Raphael's The School of Athens (c. 1510)

Late in his career (possibly about 135 BC) Hipparchus compiled his star catalog, the original of which does not survive. He also constructed a celestial globe depicting the constellations, based on his observations. His interest in the fixed stars may have been inspired by the observation of a supernova (according to Pliny), or by his discovery of precession, according to Ptolemy, who says that Hipparchus could not reconcile his data with earlier observations made by Timocharis and Aristillus. For more information see Discovery of precession. In Raphael's painting The School of Athens, Hipparchus is depicted holding his celestial globe, as the representative figure for astronomy.[36]

Previously, Eudoxus of Cnidus in the 4th century BC had described the stars and constellations in two books called Phaenomena and Entropon. Aratus wrote a poem called Phaenomena or Arateia based on Eudoxus's work. Hipparchus wrote a commentary on the Arateia – his only preserved work – which contains many stellar positions and times for rising, culmination, and setting of the constellations, and these are likely to have been based on his own measurements.

Hipparchus made his measurements with an armillary sphere, and obtained the positions of at least 850 stars. It is disputed which coordinate system(s) he used. Ptolemy's catalog in the Almagest, which is derived from Hipparchus's catalog, is given in ecliptic coordinates. However Delambre in his Histoire de l'Astronomie Ancienne (1817) concluded that Hipparchus knew and used the equatorial coordinate system, a conclusion challenged by Otto Neugebauer in his A History of Ancient Mathematical Astronomy (1975). Hipparchus seems to have used a mix of ecliptic coordinates and equatorial coordinates: in his commentary on Eudoxos he provides stars' polar distance (equivalent to the declination in the equatorial system), right ascension (equatorial), longitude (ecliptical), polar longitude (hybrid), but not celestial latitude.

As with most of his work, Hipparchus's star catalog was adopted and perhaps expanded by Ptolemy. Delambre, in 1817, cast doubt on Ptolemy's work. It was disputed whether the star catalog in the Almagest is due to Hipparchus, but 1976–2002 statistical and spatial analyses (by R. R. Newton, Dennis Rawlins, Gerd Grasshoff,[37] Keith Pickering[38] and Dennis Duke[39]) have shown conclusively that the Almagest star catalog is almost entirely Hipparchan. Ptolemy has even (since Brahe, 1598) been accused by astronomers of fraud for stating (Syntaxis, book 7, chapter 4) that he observed all 1025 stars: for almost every star he used Hipparchus's data and precessed it to his own epoch ​2 2⁄3 centuries later by adding 2°40' to the longitude, using an erroneously small precession constant of 1° per century.

In any case the work started by Hipparchus has had a lasting heritage, and was much later updated by Al Sufi (964) and Copernicus (1543). Ulugh Beg reobserved all the Hipparchus stars he could see from Samarkand in 1437 to about the same accuracy as Hipparchus's. The catalog was superseded only in the late 16th century by Brahe and Wilhelm IV of Kassel via superior ruled instruments and spherical trigonometry, which improved accuracy by an order of magnitude even before the invention of the telescope. Hipparchus is considered the greatest observational astronomer from classical antiquity until Brahe.[40]
Stellar magnitude

Hipparchus is only conjectured to have ranked the apparent magnitudes of stars on a numerical scale from 1, the brightest, to 6, the faintest.[41] Nevertheless, this system certainly precedes Ptolemy, who used it extensively about AD 150.[41] This system was made more precise and extended by N. R. Pogson in 1856, who placed the magnitudes on a logarithmic scale, making magnitude 1 stars 100 times brighter than magnitude 6 stars, thus each magnitude is 5√100 or 2.512 times brighter than the next faintest magnitude.[42]
Precession of the equinoxes (146–127 BC)
See also: Precession (astronomy)

Hipparchus is generally recognized as discoverer of the precession of the equinoxes in 127 BC.[43] His two books on precession, On the Displacement of the Solsticial and Equinoctial Points and On the Length of the Year, are both mentioned in the Almagest of Claudius Ptolemy. According to Ptolemy, Hipparchus measured the longitude of Spica and Regulus and other bright stars. Comparing his measurements with data from his predecessors, Timocharis and Aristillus, he concluded that Spica had moved 2° relative to the autumnal equinox. He also compared the lengths of the tropical year (the time it takes the Sun to return to an equinox) and the sidereal year (the time it takes the Sun to return to a fixed star), and found a slight discrepancy. Hipparchus concluded that the equinoxes were moving ("precessing") through the zodiac, and that the rate of precession was not less than 1° in a century.
Geography

Hipparchus's treatise Against the Geography of Eratosthenes in three books is not preserved.[44] Most of our knowledge of it comes from Strabo, according to whom Hipparchus thoroughly and often unfairly criticized Eratosthenes, mainly for internal contradictions and inaccuracy in determining positions of geographical localities. Hipparchus insists that a geographic map must be based only on astronomical measurements of latitudes and longitudes and triangulation for finding unknown distances. In geographic theory and methods Hipparchus introduced three main innovations.[45]

He was the first to use the grade grid, to determine geographic latitude from star observations, and not only from the Sun's altitude, a method known long before him, and to suggest that geographic longitude could be determined by means of simultaneous observations of lunar eclipses in distant places. In the practical part of his work, the so-called "table of climata", Hipparchus listed latitudes for several tens of localities. In particular, he improved Eratosthenes' values for the latitudes of Athens, Sicily, and southern extremity of India.[46] In calculating latitudes of climata (latitudes correlated with the length of the longest solstitial day), Hipparchus used an unexpectedly accurate value for the obliquity of the ecliptic, 23°40' (the actual value in the second half of the 2nd century BC was approximately 23°43'), whereas all other ancient authors knew only a roughly rounded value 24°, and even Ptolemy used a less accurate value, 23°51'.[47]

Hipparchus opposed the view generally accepted in the Hellenistic period that the Atlantic and Indian Oceans and the Caspian Sea are parts of a single ocean. At the same time he extends the limits of the oikoumene, i.e. the inhabited part of the land, up to the equator and the Arctic Circle.[48] Hipparchus' ideas found their reflection in the Geography of Ptolemy. In essence, Ptolemy's work is an extended attempt to realize Hipparchus' vision of what geography ought to be.
Legacy

He is depicted opposite Ptolemy in Raphael's painting The School of Athens, although this figure is popularly believed to be Strabo or Zoroaster.[49]

The rather cumbersome formal name for the ESA's Hipparcos Space Astrometry Mission was High Precision Parallax Collecting Satellite; it was deliberately named in this way to give an acronym, HiPParCoS, that echoed and commemorated the name of Hipparchus. The lunar crater Hipparchus and the asteroid 4000 Hipparchus are more directly named after him.

He was inducted into the International Space Hall of Fame in 2004.[50]
Monument

The Astronomer's Monument at the Griffith Observatory in Los Angeles, California, United States features a relief of Hipparchus as one of six of the greatest astronomers of all time and the only one from Antiquity.
Editions and translations

Berger H. Die geographischen Fragmente des Hipparch. Leipzig: B. G. Teubner, 1869.
Dicks D.R. The Geographical Fragments of Hipparchus. Edited with an Introduction and Commentary. London: Athlon Press, 1960. Pp. xi + 215.
Manitius K. In Arati et Eudoxi Phaenomena commentariorum libri tres. Leipzig: B. G. Teubner, 1894. 376 S.

See also

Aristarchus of Samos, a Greek mathematician who calculated the distance from the Earth to the sun
Eratosthenes, a Greek mathematician who calculated the distance from the Earth to the sun
Greek mathematics
On the Sizes and Distances (Aristarchus)
On the Sizes and Distances (Hipparchus)
Posidonius, a Greek philosopher who calculated the circumference of the Earth

Notes

These figures use modern dynamical time, not the solar time of Hipparchus's era. E.g., the true 4267-month interval was nearer 126,007 days plus a little over half an hour.

References
Citations

C. M. Linton (2004). From Eudoxus to Einstein: a history of mathematical astronomy. Cambridge University Press. p. 52. ISBN 978-0-521-82750-8.
G J Toomer's chapter "Ptolemy and his Greek Predecessors" in "Astronomy before the Telescope", British Museum Press, 1996, p. 81.
Stephen C. McCluskey (2000). Astronomies and cultures in early medieval Europe. Cambridge University Press. p. 22. ISBN 978-0-521-77852-7.
Jones, Alexander Raymond (2017). Hipparchus. Encyclopedia Britannica, Inc. Archived from the original on 6 August 2017. Retrieved 25 August 2017.
G. J. Toomer, "Hipparchus" (1978); and A. Jones, "Hipparchus."
"Hipparchus of Nicea". Ancient History Encyclopedia. Archived from the original on 5 June 2016. Retrieved 5 June 2016.
Modern edition: Karl Manitius (In Arati et Eudoxi Phaenomena, Leipzig, 1894).
D.Rawlins Archived 21 May 2006 at the Wayback Machine, "Farnese Atlas Celestial Globe, Proposed Astronomical Origins", 2005.
B. E. Schaefer Archived 14 January 2005 at the Wayback Machine, "Epoch of the Constellations on the Farnese Atlas and their Origin in Hipparchus's Lost Catalog", Journal for the History of Astronomy, May 2005 versus Dennis Duke Archived 14 August 2007 at the Wayback Machine Journal for the History of Astronomy, February 2006.
Lucio Russo, The Forgotten Revolution: How Science Was Born in 300 BCE and Why It Had To Be Reborn, (Berlin: Springer, 2004). ISBN 3-540-20396-6, pp. 286–293.
Lucio Russo, The Forgotten Revolution: How Science Was Born in 300 BCE and Why It Had To Be Reborn, (Berlin: Springer, 2004). ISBN 3-540-20396-6, pp. 365–379.
Mott Greene, "The birth of modern science?" Review of The Forgotten Revolution, Nature 430 (5 August 2004): 614.
Stanley, Richard P. (1997), "Hipparchus, Plutarch, Schröder, and Hough" (PDF), The American Mathematical Monthly, 104 (4): 344–350, CiteSeerX 10.1.1.39.7346, doi:10.2307/2974582, JSTOR 2974582, MR 1450667, archived (PDF) from the original on 14 May 2011
Acerbi, F. (2003), "On the shoulders of Hipparchus: A reappraisal of ancient Greek combinatorics" (PDF), Archive for History of Exact Sciences, 57 (6): 465–502, doi:10.1007/s00407-003-0067-0, S2CID 122758966, archived from the original (PDF) on 21 July 2011
For more information see G. J. Toomer, "Hipparchus and Babylonian astronomy."
Franz Xaver Kugler, Die Babylonische Mondrechnung ("The Babylonian lunar computation"), Freiburg im Breisgau, 1900.
Aaboe, Asger (1955), "On the Babylonian origin of some Hipparchian parameters", Centaurus, 4 (2): 122–125, Bibcode:1955Cent....4..122A, doi:10.1111/j.1600-0498.1955.tb00619.x. On p. 124, Aaboe identifies the Hipparchian equation 5458 syn. mo. = 5923 drac. mo. with the equation of 1,30,58 syn. mo. = 1,38,43 drac. mo. (written in sexagesimal) which he cites to p. 73 of Neugebauer's Astronomical Cuneiform Texts, London 1955.
Pro & con arguments are given at DIO volume 11 number 1 Archived 26 April 2015 at the Wayback Machine article 3 sections C & D.
See demonstration Archived 2 April 2015 at the Wayback Machine of reverse use of Hipparchus's table for the 1245 BCE eclipse.
Toomer, "The Chord Table of Hipparchus" (1973).
Klintberg, Bo C. (2005). "Hipparchus's 3600′-Based Chord Table and Its Place in the History of Ancient Greek and Indian Trigonometry". Indian Journal of History of Science. 40 (2): 169–203.
Dennis Rawlins, "Aubrey Diller Legacies" Archived 9 May 2010 at the Wayback Machine, DIO 5 (2009); Shcheglov D.A. (2002–2007): "Hipparchus’ Table of Climata and Ptolemy’s Geography", Orbis Terrarum 9 (2003–2007), 177–180.
Dennis Rawlins, "Hipparchos' Eclipse-Based Longitudes: Spica & Regulus" Archived 26 July 2011 at the Wayback Machine, DIO 16 (2009).
Detailed dissents on both values are presented in DIO volume 11 number 1 Archived 26 April 2015 at the Wayback Machine articles 1 & 3 and DIO volume 20 article 3 section L. See also these analyses' summary Archived 2 April 2015 at the Wayback Machine.
Footnote 18 Archived 26 April 2015 at the Wayback Machine of DIO 6 (1996).
Stephenson & Fatoohi 1993; Steele et al. 1997
Chapront et al. 2002
Summarized in Hugh Thurston (2002): Isis 93, 58–69.
Toomer, 1967
Explained at equation 25 of a recent investigation Archived 6 February 2015 at the Wayback Machine, paper #2.
Leverington, David (2003), Babylon to Voyager and Beyond: A History of Planetary Astronomy, Cambridge University Press, p. 30, ISBN 9780521808408.
DIO Archived 29 February 2008 at the Wayback Machine, volume 1, number 1, pages 49–66; A.Jones, 2001; Thurston, op. cit., page 62
Thurston, op. cit., page 67, note 16. R. Newton proposed that Hipparchus made an error of a degree in one of the trios' eclipses. D.Rawlins's theory (Thurston op. cit.) that Hipparchus analysed the two trios in pairs not threesomes provides a possible explanation for the one degree slip. It was a fudge Archived 24 January 2018 at the Wayback Machine necessitated by inadequacies of analysing by pairs instead of using the better method Ptolemy applies at Almagest Book 4 Parts 6 and 11.
Ibid, note 14; Jones 2001
"Five Millennium Catalog of Solar Eclipses". Archived from the original on 25 April 2015. Retrieved 11 August 2009., #04310, Fred Espenak, NASA/GSFC
Swerdlow, N. M. (August 1992), "The Enigma of Ptolemy's Catalogue of Stars", Journal for the History of Astronomy, 23 (3): 173–183, Bibcode:1992JHA....23..173S, doi:10.1177/002182869202300303, S2CID 116612700
Gerd Grasshoff: The history of Ptolemy's star catalogue, Springer, New York, 1990, ISBN 3-540-97181-5 (Analyse des im "Almagest" überlieferten Sternenkatalogs)
"Keith Pickering" (PDF). Archived (PDF) from the original on 5 June 2012. Retrieved 6 August 2012.
"The Measurement Method of the Almagest Stars" Archived 12 June 2010 at the Wayback Machine, by Dennis Duke Archived 7 June 2007 at the Wayback Machine, DIO: the International Journal of Scientific History,12 (2002).
Benson Bobrick, The Fated Sky, Simon & Schuster, 2005, p 151
Ptolemy (1998), Ptolemy's Almagest, translated by Toomer, G. J., Princeton University Press, pp. 16, 341–399, ISBN 0-691-00260-6, "The magnitudes range (according to a system which certainly precedes Ptolemy, but is only conjecturally attributed to Hipparchus) from 1 to 6." Quote by Toomer, not Ptolemy.
Pogson, N. R. (1856). "Magnitudes of Thirty-six of the Minor Planets for the first day of each month of the year 1857". MNRAS. 17: 12. Bibcode:1856MNRAS..17...12P. doi:10.1093/mnras/17.1.12.
Alexander Jones "Ptolemy in Perspective: Use and Criticism of his Work from Antiquity to the Nineteenth Century, Springer, 2010, p.36.
Editions of fragments: Berger H. Die geographischen Fragmente des Hipparch. Leipzig: B. G. Teubner, 1869.; Dicks D.R. The Geographical Fragments of Hipparchus. London: Athlon Press, 1960.
On Hipparchus's geography see: Berger H. Die geographischen Fragmente des Hipparch. Leipzig: B. G. Teubner, 1869.; Dicks D.R. The Geographical Fragments of Hipparchus. London: Athlon Press, 1960; Neugebauer O. A History of Ancient Mathematical Astronomy. Pt. 1–3. Berlin, Heidelberg, New York: Springer Verlag, 1975: 332–338; Shcheglov D.A. Hipparchus’ "Table of Climata and Ptolemy’s Geography". Orbis Terrarum 9. 2003–2007: 159–192.
Shcheglov D.A. "Hipparchus on the Latitude of Southern India". Greek, Roman, and Byzantine Studies 45. 2005: 359–380; idem. "Eratosthenes' Parallel of Rhodes and the History of the System of Climata Archived 16 July 2017 at the Wayback Machine". Klio 88. 2006: 351–359.; idem. "Hipparchus’ Table of Climata and Ptolemy’s Geography". Orbis Terrarum 9. 2003–2007: 159–192.
Diller A. (1934). "Geographical Latitudes in Eratosthenes, Hipparchus and Posidonius". Klio 27.3: 258–269; cf. Shcheglov D.A. "Hipparchus’ Table of Climata and Ptolemy’s Geography", 177–180.
Shcheglov D.A. "Ptolemy’s Latitude of Thule and the Map Projection in the Pre-Ptolemaic Geography". Antike Naturwissenschaft und ihre Rezeption (AKAN) 17. 2007: 132–139.
Swerdlow, N. M. (1992). "The Enigma of Ptolemy's Catalogue of Stars". Journal for the History of Astronomy. 23 (3): 173–183. doi:10.1177/002182869202300303. S2CID 116612700.

"X-Prize Group Founder to Speak at Induction". El Paso Times. El Paso, Texas. 17 October 2004. p. 59 – via Newspapers.com.

Sources

Works cited

Acerbi F. (2003). "On the shoulders of Hipparchus: A reappraisal of ancient Greek combinatorics". Archive for History of Exact Sciences 57: 465–502.
Bianchetti S. (2001). "Dall’astronomia alla cartografia: Ipparco di Nicea". ПОΙΚΙΛΜΑ. Studi in onore di Michelle R. Cataudella in occasione del 60° compleanno. La Spezia: Agorà Edizioni: 145–156.
Bowen A.C., Goldstein B.R. (1991). "Hipparchus' Treatment of Early Greek Astronomy: The Case of Eudoxus and the Length of Daytime Author(s)". Proceedings of the American Philosophical Society 135(2): 233–254.
Chapront J., Touze M. Chapront, Francou G. (2002): "A new determination of lunar orbital parameters, precession constant, and tidal acceleration from LLR measurements". Astronomy and Astrophysics 387: 700–709.
Dicks D.R. (1960). The Geographical Fragments of Hipparchus. London: Athlon Press. Pp. xi, 215.
Diller A. (1934). "Geographical Latitudes in Eratosthenes, Hipparchus and Posidonius". Klio 27(3): 258–269.
Duke D.W. (2002). "Associations between the ancient star catalogs". Archive for the History of Exact Sciences 56(5):435–450. (Author's draft here.)
Honigmann E. (1929). Die sieben Klimata und die πολεις επισημοι. Eine Untersuchung zur Geschichte der Geographie und Astrologie in Altertum und Mittelalter. Heidelberg: Carl Winter's Universitätsbuchhandlung. 247 S.
Jones A. (2001). "Hipparchus." In Encyclopedia of Astronomy and Astrophysics. Nature Publishing Group.
Moore P. (1994). Atlas of the Universe, Octopus Publishing Group LTD (Slovene translation and completion by Tomaž Zwitter and Savina Zwitter (1999): Atlas vesolja): 225.
Nadal R., Brunet J.P. (1984). "Le "Commentaire" d'Hipparque. I. La sphère mobile. Archive for History of Exact Sciences 29: 201–236.
Neugebauer O. (1975). A History of Ancient Mathematical Astronomy. Vol. 1–3. Berlin, Heidelberg, New York: Springer Verlag.
Newton R.R. (1977). The Crime of Claudius Ptolemy. Baltimore: Johns Hopkins University Press.
Rawlins D. (1982). An Investigation of the Ancient Star Catalog. Proceedings of the Astronomical Society of the Pacific 94, 359–373. Has been updated several times: DIO, volume 8, number 1 (1998), page 2, note 3, and DIO, volume 10 (2000), page 79, note 177.
Russo L. (1994). "The astronomy of Hipparchus and his time: A study based on pre-ptolemaic sources". Vistas in Astronomy 38.2: 207–248
Schaefer B.E. (2005). "The Epoch of the Constellations on the Farnese Atlas and their Origin in Hipparchus's Lost Catalogue". Journal for the History of Astronomy 36.2: 167–196.
Shcheglov D.A. (2005). "Hipparchus on the Latitude of Southern India". Greek, Roman, and Byzantine Studies 45: 359–380.
Shcheglov D.A. (2006). “Eratosthenes’ Parallel of Rhodes and the History of the System of Climata”. Klio 88: 351–359.
Shcheglov D.A. (2007). "Ptolemy’s Latitude of Thule and the Map Projection in the Pre-Ptolemaic Geography". Antike Naturwissenschaft und ihre Rezeption (AKAN) 17: 121–151.
Shcheglov D.A. (2003–2007). "Hipparchus’ Table of Climata and Ptolemy’s Geography". Orbis Terrarum 9: 159–192.
Sidoli N. (2004). "Hipparchus and the Ancient Metrical Methods on the Sphere". Journal for the History of Astronomy 35: 71–84.
Steele J.M., Stephenson F.R., Morrison L.V. (1997). "The accuracy of eclipse times measured by the Babylonians". Journal for the History of Astronomy 28, 337..345
Stephenson F.R., Fatoohi L.J. (1993). "Lunar Eclipse Times Recorded in Babylonian History". Journal for the History of Astronomy 24: 255..267
Swerdlow N.M. (1969). "Hipparchus on the distance of the sun." Centaurus 14: 287–305.
Toomer G.J. (1967). "The Size of the Lunar Epicycle According to Hipparchus." Centaurus 12: 145–150.
Toomer G.J. (1973). "The Chord Table of Hipparchus and the Early History of Greek Trigonometry." Centaurus 18: 6–28.
Toomer G.J. (1974). "Hipparchus on the Distances of the Sun and Moon." Archives for the History of the Exact Sciences 14: 126–142.
Toomer G.J. (1978). "Hipparchus." In Dictionary of Scientific Biography 15: 207–224.
Toomer G.J. (1980). "Hipparchus' Empirical Basis for his Lunar Mean Motions," Centaurus 24: 97–109.
Toomer G.J. (1988). "Hipparchus and Babylonian Astronomy." In A Scientific Humanist: Studies in Memory of Abraham Sachs, ed. Erle Leichty, Maria deJ. Ellis, and Pamel Gerardi. Philadelphia: Occasional Publications of the Samuel Noah Kramer Fund, 9.
Wolff M. (1989). "Hipparchus and the Stoic Theory of Motion". In Matter and Metaphysics. Ed. J. Barnes & M. Mignucci. Napoli: Bibliopolis: 346–419.

Further reading
Dreyer, John L.E (1953). A History of Astronomy from Thales to Kepler. New York: Dover Publications.
Heath, Thomas (1921). A History of Greek Mathematics. Oxford: Clarendon Press.
Lloyd, G.E.R. (1973). Greek science after Aristotle. New York: Norton. ISBN 978-0-393-04371-6.
Neugebauer, Otto (1956). "Notes on Hipparchus". In Weinberg, Saul S (ed.). The Aegean and the Near East: Studies Presented to Hetty Goldman. Locust Valley, NY: J.J. Augustin.
Ptolemy (1984). Ptolemy's Almagest. G.J. Toomer, trans. New York: Springer-Verlag. ISBN 978-0-387-91220-2.
Thomson, J.Oliver (1948). History of Ancient Geography. Cambridge: Cambridge University Press.

---

Aglaonice Agrippa Anaximander Andronicus Apollonius Aratus Aristarchus Aristyllus Attalus Autolycus Bion Callippus Cleomedes Cleostratus Conon Eratosthenes Euctemon Eudoxus Geminus Heraclides Hicetas Hipparchus Hippocrates of Chios Hypsicles Menelaus Meton Oenopides Philip of Opus Philolaus Posidonius Ptolemy Pytheas Seleucus Sosigenes of Alexandria Sosigenes the Peripatetic Strabo Thales Theodosius Theon of Alexandria Theon of Smyrna Timocharis

----

Ancient Greek and Hellenistic mathematics (Euclidean geometry)
Mathematicians
(timeline)
Anaxagoras Anthemius Archytas Aristaeus the Elder Aristarchus Apollonius Archimedes Autolycus Bion Bryson Callippus Carpus Chrysippus Cleomedes Conon Ctesibius Democritus Dicaearchus Diocles Diophantus Dinostratus Dionysodorus Domninus Eratosthenes Eudemus Euclid Eudoxus Eutocius Geminus Heliodorus Heron Hipparchus Hippasus Hippias Hippocrates Hypatia Hypsicles Isidore of Miletus Leon Marinus Menaechmus Menelaus Metrodorus Nicomachus Nicomedes Nicoteles Oenopides Pappus Perseus Philolaus Philon Philonides Porphyry Posidonius Proclus Ptolemy Pythagoras Serenus Simplicius Sosigenes Sporus Thales Theaetetus Theano Theodorus Theodosius Theon of Alexandria Theon of Smyrna Thymaridas Xenocrates Zeno of Elea Zeno of Sidon Zenodorus
Treatises
Almagest Archimedes Palimpsest Arithmetica Conics (Apollonius) Catoptrics Data (Euclid) Elements (Euclid) Measurement of a Circle On Conoids and Spheroids On the Sizes and Distances (Aristarchus) On Sizes and Distances (Hipparchus) On the Moving Sphere (Autolycus) Euclid's Optics On Spirals On the Sphere and Cylinder Ostomachion Planisphaerium Sphaerics The Quadrature of the Parabola The Sand Reckoner
Problems
Angle trisection Doubling the cube Squaring the circle Problem of Apollonius
Concepts/definitions
Circles of Apollonius
Apollonian circles Apollonian gasket Circumscribed circle Commensurability Diophantine equation Doctrine of proportionality Golden ratio Greek numerals Incircle and excircles of a triangle Method of exhaustion Parallel postulate Platonic solid Lune of Hippocrates Quadratrix of Hippias Regular polygon Straightedge and compass construction Triangle center
Results
In Elements
Angle bisector theorem Exterior angle theorem Euclidean algorithm Euclid's theorem Geometric mean theorem Greek geometric algebra Hinge theorem Inscribed angle theorem Intercept theorem Pons asinorum Pythagorean theorem Thales's theorem Theorem of the gnomon
Apollonius
Apollonius's theorem
Other
Aristarchus's inequality Crossbar theorem Heron's formula Irrational numbers Menelaus's theorem Pappus's area theorem Problem II.8 of Arithmetica Ptolemy's inequality Ptolemy's table of chords Ptolemy's theorem Spiral of Theodorus
Centers
Cyrene Library of Alexandria Platonic Academy
Other
Ancient Greek astronomy Greek numerals Latin translations of the 12th century Neusis construction

Retrieved from "http://en.wikipedia.org/"
All text is available under the terms of the GNU Free Documentation License