It seems to us that after the invention of writing the largest discovery was the use by humanity of the so-called decimal notation. M. V. Ostrogradsky (1801-1862)

Arithmetica, Gregor Reisch 1503. A Symbolic Image: Boethius and Pythagoras in a mathematical Competition. Pythagoras uses an Abacus, while Anicius Manlius Severinus Boethius (480 AD-524 AD) uses Numerals from India. Boethius looks very proud, he is ready while the poor Pythagoras still tries to find the solution.

"Ten is the very nature of number. All Greeks and all barbarians alike count up to ten, and having reached ten revert again to the unity. And again, Pythagoras maintains, the power of the number 10 lies in the number 4, the tetrad. This is the reason: if one starts at the unit (1) and adds the successive number up to 4, one will make up the number 10 (1+2+3+4 = 10). And if one exceeds the tetrad, one will exceed 10 too.... So that the number by the unit resides in the number 10, but potentially in the number 4. And so the Pythagoreans used to invoke the Tetrad as their most binding oath: `By him that gave to our generation the Tetractys, which contains the fount and root of eternal nature...'" (Aetius I. 3.8)

Strange enough even if 10 was a special number the Greeks used two rather complex systems of number representation. The first Herodianic, found in inscriptions and laws since the 5^th century BC represents basic numbers by the first letter of the denoting word: P for five (penta), D for ten (deka) etc. Other numbers are represented by the basic ones by juxtaposition. The system is used to represent money or weight units, accomplished by the initial letter of the denoting word: T for Talent. A Mixture of the symbols D and T is used to symbolize Deka Talents ie. ten talents. The system is also called acrophonic from acron and phone (topmost voice)

Name of Greek Letter	Greek Letter Symbol	Name of Greek Number	The Number
Iota	I	iota	1
Pi	P	pente	5
Delta	D	deka	10
Eta	H	hekaton	100
Chi	X	chilioi	1000
Mu	M	myrioi	10000

A river of fire was flowing, coming out from before him. Thousands upon thousands attended him; ten thousand times ten thousand stood before him. The court was seated, and the books were opened. Daniel 7:10. This shows that Daniel could count only up to 100 million the largest number that could be represented by conventional Greek numbers. With Archimedes many more can enter in the Paradise or the Hell.

Prometheus: Yes, and numbers, too, chiefest of
sciences, I invented for them, and the
combining of letters, creative mother
of the Muses’ arts with which to hold
all things in memory.”
Aeschylus, Prometheus Bound

The second system uses the Greek alphabet and three Phoenician letters for the 27 symbols used to represent the numbers from 1 to 10, the tenths from 20 to 100 and the hundreds from 200 to 900. Other multiples and fractions can be created by apices.

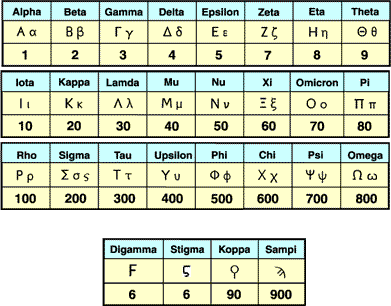
Alphanumeric system of numbers, 2 versions for 6. The Digamma looks like a double Gamma which represents 3. Note that there is no 0.

Numbers 11-19

Numbers 100-999

Combinations of Symbols for example 347 with τ for 300, μ = 40 and ζ = 7 written as: τμζ

Numbers 1000 to 9999

Using a “ι” sub- or superscript

example ^ιβτμζ for 2347 where ^ιβ is used for 2000

Numbers > 9999

Use of numbers in front (or on top) of the symbol M (myriades) who then represents the number 10000

for example γM for 30000 and γM ^ιβτμζ for 32347. An overline could be used to show that the characters represent numbers and not words.

Number larger than 10⁸

Other methods used by mathematicians such as Apollonius and Archimedes to represent numbers larger than 10⁸

Archimedes uses the myriad myriad i.e. 10000*10000 as a basis for which here I use the symbol G = 10⁸

Numbers in the range G^n-1 to Gⁿ are called n-th order numbers. This continues until the numbers of the G-th order, i.e. numbers between G^G-1 to G^G

Now I use a new Symbol P for G^G . Archimedes calles numbers up to P numbers of the first period. Then he defines a second period with numbers of the 1^st order between P and P*G, numbers of the second order between PG and P*G² until the G-th order with numbers between P*G^G-1 and P*G^G = P²

The last period is the G-th period with the G-th order numbers between P^G-1*G^G-1 to P^G

This largest Archimedes number is A myriad myriad units of myriad-times myriadth numbers of the myriad-times myriadth period

or in Greek myriakismyriostas periodou myriakismyriston arithmon myriai myriades

Diophantus extended the notion of number to include negatives and rationals, describes his symbols for exponents from -6 to 6, and notes that he moved beyond Greek traditions in permitting addition of non-homogeneous magnitudes. (Review by D. Graves of a book of I. G. Bashmakova about the Arithmetica)

Diophantus Symbols
ς	x
ΔY	x2 (dynamis) ( δύναμις)
KY	x3 (kybos) ( κύβος)
ΔYΔ	x4 (dynamodynamis) ( δυναμοδύναμις)
ΔKY	x5 (dynamokybos) ( δυναμόκυβος)
KYK	x6 (kybokybos) (κυβόκυβος )

Diophantus used for negative exponents the symbol X. For example ς^X for 1/x = x ^-1.

was used for the minus sign (a symbol derived from Lambda, I and leiyis), was used for the constant term.

K^Y αςβγ for example means x³ +2x -3.

Was the relative complex notation a problem for the development of Greek mathematics, especially algebra? Sometimes other factors may influence the development of mathematics. Keith Devlin in one of his books asked why Chinese and Japanese students are better in mathematical competitions if compared with American students. He explained that the Chinese use much easier and shorter names for numbers (for example qi for seven). The English names of the numbers 16 and 26 are sixteen and twenty six (and not six twenty) respectively, i.e there is a change of order. The Chinese word for 16 would be translated as "ten-six," and 26 as "two-ten-six." I  have some doubts if this difference of how numbers are named is so important. There are many important French mathematicians (even if the French names of numbers are complex, for example 97 is called "quatre-vingt-dix-sept" ie. "four-twenty-ten-seven").

While the ancient Greeks used to say for example triskaideka i.e. "three and ten" for the number 13 (from which the word triskaidekaphobia "The fear of 13" is derived) modern Greeks say "ten and three".

Greeks 'borrowed Egyptian numbers'

by Paul Rincon

The astronomers, physicists and mathematicians of ancient Greece were true innovators. Ancient Greeks used letters and extra symbols to represent digits. But one thing it seems the ancient Greeks did not invent was the counting system on which many of their greatest thinkers based their pioneering calculations.

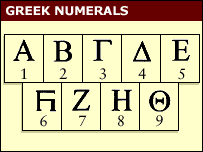
New research suggests the Greeks borrowed their system known as alphabetic numerals from the Egyptians, and did not develop it themselves as was long believed. Greek alphabetic numerals were favoured by the mathematician and physicist Archimedes, the scientific philosopher Aristotle and the mathematician Euclid, amongst others.

Trade explosion

An analysis by Dr Stephen Chrisomalis of McGill University in Montreal, Canada, showed striking similarities between Greek alphabetic numerals and Egyptian demotic numerals, used in Egypt from the late 8th Century BC until around AD 450.

Both systems use nine signs in each base so that individual units are counted 1-9, tens are counted 10-90 and so on. Both systems also lack a symbol for zero. Dr Chrisomalis proposes that an explosion in trade between Greece and Egypt after 600 BC led to the system being adopted by the Greeks.

Greek merchants may have seen the demotic system in use in Egypt and adapted it for their own purposes. "We know there was an enormous amount of contact between the Greeks and Egyptians at this time," Dr Chrisomalis told BBC News Online.

Plausible theory

Professor David Joyce, a mathematician at Clark University in Worcester, US, said he had not examined Dr Chrisomalis' research, but thought the link was plausible.

"Egyptians used hieratic and, later, demotic script where the multiple symbols looked more like single symbols," said Professor Joyce. "Instead of seven vertical strokes, a particular squiggle was used. That's the same scheme used in the Greek alphabetic numerals."

Traditionally, the system is thought to have been developed by Greeks in western Asia Minor, in modern day Turkey. Between 475 BC and 325 BC, alphabetic numerals fell out of use in favour of a system of written numbers known as acrophonic numerals. But from the late 4th Century BC onwards, alphabetic numerals became the preferred system throughout the Greek-speaking world. They were used until the fall of the Byzantine Empire in the 15th Century. The research is to be published in the journal Antiquity.

Quotations

The ingenious method of expressing every possible number using a set of ten symbols (each symbol having a place value and an absolute value) emerged in India. The idea seems so simple nowadays that its significance and profound importance is no longer appreciated. Its simplicity lies in the way it facilitated calculation and placed arithmetic foremost amongst useful inventions. the importance of this invention is more readily appreciated when one considers that it was beyond the two greatest men of Antiquity, Archimedes and Apollonius. Laplace

Then Palamedes, whenever he appears in tragedy, proves Agamemnon ridiculously unfit to be a general. Did you never remark how he declares that he had invented number, and had numbered the ships and set in array the ranks of the army at Troy; which implies that they had never been numbered before, and Agamemnon must be supposed literally to have been incapable of counting his own feet--how could he if he was ignorant of number? And if that is true, what sort of general must he have been? Plato, Republic

LINKS

• Archimedes Mathematics , Archimedes and Combinatorial Problems (The loculus of Archimedes)
• Archimedes the Arbelos and the Salinon , Archimedes semi-regular Convex Solids , Archimedes Cubic and Quadric Equations
• Archimedes and the Palimpsest , The death of Archimedes, a transition to a new era