Archimedes der Mathematiker

Archidamos III, the King of Sparta (often wrongly used as an image of the Mathematician Archimedes) on the cover of a Japanese Basic Calculus book.

Archimedes of Syracuse (Αρχιμήδης ο Συρακούσιος) (287 – 212) BC, son of the astronomer Phidias (according to the text of the Sand Reckoner) worked as an "engineering consultant" to the king, inventing many devices for military defense of the city such as catapults, iron claws and also probably an odometer and planetaria. Most of all he was a mathematician and a mathematical physicist.

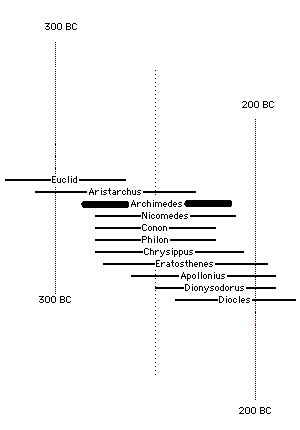
Timeline: Archimedes and contemporary ancient scientists from http://www-groups.dcs.st-and.ac.uk/~history/Timelines/index.html

He was killed according to a legend by a Roman soldier in 212 BC. Archimedes visited Alexandria in Egypt to study the texts at the great Library of Alexandria, where Euclid had worked. He was a friend of Eratosthenes of Cyrene and Conon of Samos.

In dividing volumes and areas into the sum of a large number of individual pieces Archimedes was essentially using the calculus 2000 years before Newton (1643 - 1727) and Leibniz (1646 – 1716). Archimedes found that:

• On the sphere and cylinder (Περί σφαίρας &kappaαι κυλίνδρου ). If a sphere is inscribed in a cylinder, then the sphere is 2/3 of the cylinder in both surface area and volume.

  ... &Piολλῶν δὲ καὶ &kappaαλῶν εὑρέτης &gammaεγόνως λέγεται &tauῶν φίλων δεηθῆναι &kappaαὶ τῶν συγγενῶν, ὅπως αὐτοῦ μετὰ &tauὴν τελευτὴν ἐπιστήσωσι τῶι &tauάφωι τὸν περιλαμβάνοντα &tauὴν σφαῖραν ἐντὸς &kappaύλινδον, ἐπιγράψαντες &tauὸν λόγον τῆς ὑπεροχῆς τοῦ &piεριέχοντος &sigmaτερεοῦ πρὸς &tauὸ περιεχόμενον. Plutarchi vitae parallelae, Marcellus ed. C. Sintenis, Lipsiae 1867

Perhaps the best indication of what Archimedes truly loved most is his request that his tombstone include a cylinder circumscribing a sphere, accompanied by the inscription of his amazing theorem that the sphere is exactly two-thirds of the circumscribing cylinder in both surface area and volume!" (Laubenbacher and Pengelley, p. 95). Archimedes knew that he provided a proof:

By nature, these properties had existed before for these figures, . . . but it happened that all missed this and nobody realized this
Archimedes, De sphaera et cylindro 1, pp. 2f. Heiberg; Cf. W. Burkert, “Konstruktion und Seinsstruktur: Praxis und Platonismus in der griechischen Mathematik,” Abhandlungen der Braunschweigischen Wissenschaftlichen Gesellschaft 34 (1982): 125–41.

Maybe this inspired Gauss to use a geometric figure for his tombstone as he discovered another regular polygon not known by the Greeks after 2000 years and was probably very proud about this. See: An incredible discovery of Archimedes by Jeremy Batterson

• On Spirals (Περί &epsilonλίκων) The area of the spiral is 1/3 the area of the circle (where only a revolution is considered for the spiral)

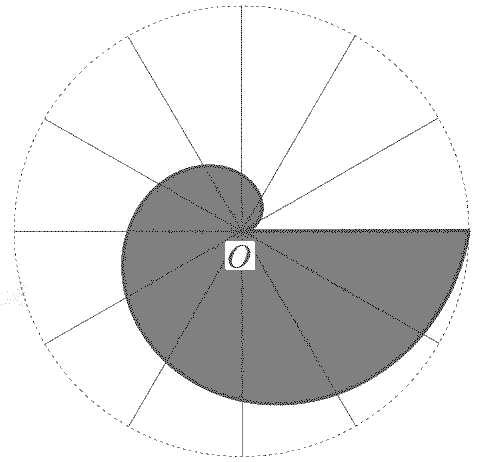
That is, the area enclosed by the spiral arc of one revolution is one third of the area of the circle with center at the origin and of radius at the terminus of the spiral arc. The Archimedes spiral is given by r = aq. At q=2p new have a radius r = 2apq. The area of the circle is p(2apq)². For the area of the spiral of one revolution we have to integrate the function f²(q) with q from 0 to 2p, where f(q) = aq.

• The volume of the sphere with radius r is (4pr³)/3 and its area is 4pr²

To prove this he approximated the sphere by cones and frustrums (truncated cones). The more frustrums are used the better the sphere is approximated. He drew two shapes around the sphere's center. He used frustrums inscribed and circumscribed. He used these shapes to obtain the upper and lower limit of the sphere area and surface.

• Quadrature of the parabola (Τετραγωνισμός &piαραβολής ). The area enclosed by a parabola and a straight line is 4/3 the area of a triangle with equal base and height.

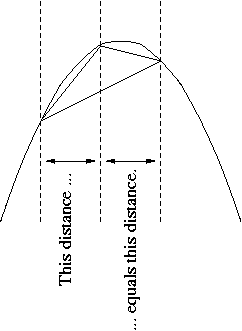
The "base" is any secant line, not necessarily orthogonal to the parabola's axis; "the same base" means the same "horizontal" component of the length of the base; "horizontal" means orthogonal to the axis. "Height" means the length of the segment parallel to the axis from the vertex to the base. The vertex must be so placed that the two horizontal distances mentioned in the illustration are equal. For the proof he calculated the oldest known example of a geometric series with the ratio 1/4:

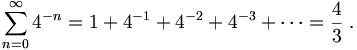
Actually he did not calculate this infinite sum avoiding to consider infinite terms. If the first term in this series is the area of the triangle in the illustration then the second is the sum of the areas of two triangles whose bases are the two smaller secant lines in the illustration.

(Scan from T. L. Heath's translation into English of Archimedes' collected works, published in 1897 by Cambridge University Press)

See: Details of the Quadrature of the Parabola by Archimedes

• On conoids and spheroids (Περί &kappaωνοειδέων &kappaαι σφαιροειδέων) He calculated the ratio of volumes of objects obtained by rotation of some type of curves around an axis.

Take a square with side a, a circle k, a parabola and the diagonal d as shown in the Figure below. A complete rotation of these curves around the x-axis will produce a cylinder, a semi-sphere, a paraboloid and a cone that have volume ratios as 6:4:3:2.

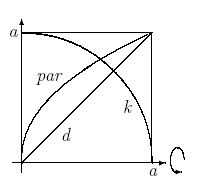
• The area of the triangle ABC is exactly three times the area bounded by the parabola and the secant line AB.

The points A and B are on a parabola curve. The line AC is parallel to the axis of the parabola. The line BC is tangent to the parabola.

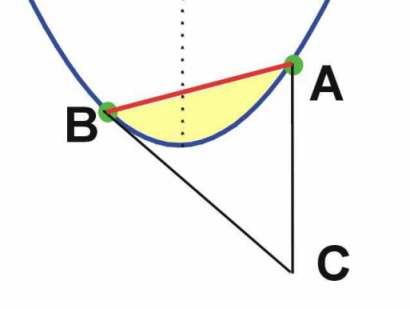
The yellow area is 1/3 of the area of the triangle ABC

See a scanned version of T. L. Heath's translation into English of Archimedes' collected works, published in 1897 by Cambridge University Press

Part 2

The death of Archimedes, a transition to a new era

Recursive Functions (including Archimedes Psammites) Stanford Encyclopedia of Philosophy

Archimedes and Combinatorial Problems (The loculus of Archimedes)

Archimedes the Arbelos and the Salinon

Archimedes semi-regular Convex Solids

Archimedes Cubic and Quadric Equations