.

Griechische Mathematik: Archimedes - Kubische und biquadratische Gleichungen

They were very upset when I said the development of the greatest importance to mathematics in Europe was the discovery by Tartaglia that you can solve a cubic equation: although it is of little use in itself, the discovery must have been psychologically wonderful because it showed that a modern man could do something no ancient Greek could do. It therefore helped in the Renaissance, which was freeing man from the intimidation of the ancients. What the Greeks are learning in school is to be intimidated into thinking that they have fallen so far below their ancestors. [From: "Cubic Equations, or Where Did the Examination Question Come From?" (by H. B. Griffiths and A. E. Hirst (quoting Richard Feynman reporting on a 1980 visit to Greece), American Mathematical Monthly, February 1994, pp.151-161 ]

The three most famous mathematical problems of Ancient Greeks were:

We know that these problems cannot be solved using Plato and Euclid's restriction that only a compass and a straightedge should be used. While this seems too be an academic restriction it is a “scientific” approach not found in Babylonian or Egyptian mathematics. Pappus one of the last ancient Greek mathematicians called problems that can be solved by compass and straightedge a plane problem. Further a problem that requires one or more conic sections was called a solid problem and the other problems were called linear problems.

Archimedes of Syracuse provided a non-Platonic solution for the angle trisection problem.

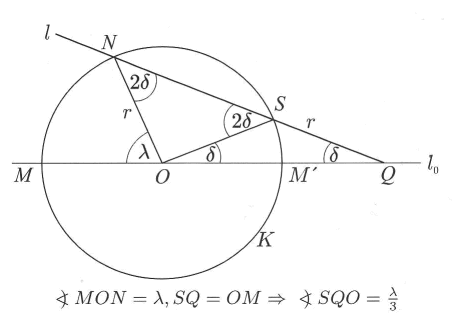
Take a circle K and an angle MON with 0^o < λ < 90^o. Archimedes says without proof that: A point S exists such that the line NS cuts the line l₀ through MM' in Q with QS = r, where r is the circle radius. Then SQO is λ/3 and this can be algebraically described as a solution of the cubic equation:

x³-3r²x-2r³cos(λ)=0

In this way Archimedes provided probably one of the simplest geometric “solutions” of the angle trisection problem.

Note that the geometric construction requires a marked straightedge which is not allowed by idealists like Plato. For the geometric construction it is required to mark a distance equal to the circle radius on the straightedge. The straightedge requires two marks (notched in two places). The Greeks called such constructions neusis (νεύσης) or "verging" constructions.

In On Spirals, according to Heath, Archimedes says that: If N is some point on a circle K and given a distance α, where N is not M, see Figure above then:

A line l exists through N that cuts the circle K in a point S and l₀ outside the circle in Q such that QS = α. Where l₀is a line through MM'.

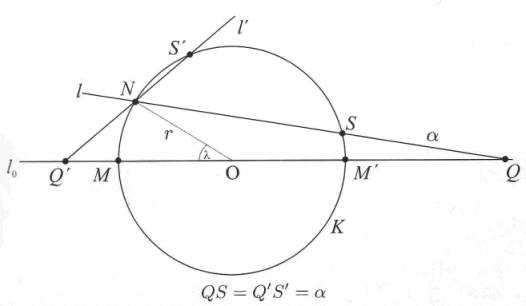
Actually another line l' exists that goes through the point N and that intersects the circle in S' and the line l0 in Q' such that Q'S' = QS = α.

The algebraic analog of this geometric problem can be formulated as a bi-quadratic equation:

This equation according to the statement of Archimedes has for α < 0 exactly a real root in (-infinite , -r) and exactly one real root in (r, +infinite). Even if Archimedes did not provide a proof for these geometrical problems he knew indirect that for specific equations of third and fourth degree real solutions always exist, even if he did not use the algebraic notation.

Greeks therefore consider problems with third and fourth order polynomials but mainly geometrically. The lack of an algebraic notation that appeared only very late with Diophantus probably can be explained by the discovery of the irrationals. To some extend also the Platonic ideal was responsible for considering mainly geometric problems. Also the complex and sometimes not standardized notation of numbers could be responsible that geometry was more advanced than algebra.

For more information see: Constructions Using a Compass and Twice-Notched Straightedge (PDF File)

Archimedes Cubic and Quadric Equations

Michael Lahanas

Αρχιμήδης ο Μαθηματικός: εξισώσεις τρίτου και τετάρτου βαθμού

.