Yang–Mills theory

Yang–Mills theory is a gauge theory based on a special unitary group SU(N ), or more generally any compact, reductive Lie algebra. Yang–Mills theory seeks to describe the behavior of elementary particles using these non-abelian Lie groups and is at the core of the unification of the electromagnetic force and weak forces (i.e. U(1) × SU(2)) as well as quantum chromodynamics, the theory of the strong force (based on SU(3)). Thus it forms the basis of our understanding of the Standard Model of particle physics.

History and theoretical description

In a private correspondence, Wolfgang Pauli formulated in 1953 a six-dimensional theory of Einstein's field equations of general relativity, extending the five-dimensional theory of Kaluza, Klein, Fock and others to a higher-dimensional internal space.[1] However, there is no evidence that Pauli developed the Lagrangian of a gauge field or the quantization of it. Because Pauli found that his theory "leads to some rather unphysical shadow particles", he refrained from publishing his results formally.[1] Although Pauli did not publish his six-dimensional theory, he gave two talks about it in Zürich.[2] Recent research shows that an extended Kaluza–Klein theory is in general not equivalent to Yang–Mills theory, as the former contains additional terms.[3]

In early 1954, Chen Ning Yang and Robert Mills[4] extended the concept of gauge theory for abelian groups, e.g. quantum electrodynamics, to nonabelian groups to provide an explanation for strong interactions. The idea by Yang–Mills was criticized by Pauli,[5] as the quanta of the Yang–Mills field must be massless in order to maintain gauge invariance. The idea was set aside until 1960, when the concept of particles acquiring mass through symmetry breaking in massless theories was put forward, initially by Jeffrey Goldstone, Yoichiro Nambu, and Giovanni Jona-Lasinio.

This prompted a significant restart of Yang–Mills theory studies that proved successful in the formulation of both electroweak unification and quantum chromodynamics (QCD). The electroweak interaction is described by the gauge group SU(2) × U(1), while QCD is an SU(3) Yang–Mills theory. The massless gauge bosons of the electroweak SU(2) × U(1) mix after spontaneous symmetry breaking to produce the 3 massive weak bosons (W+ ,W−, and Z) as well as the still-massless photon field. The dynamics of the photon field and its interactions with matter are, in turn, governed by the U(1) gauge theory of quantum electrodynamics. The Standard Model combines the strong interaction with the unified electroweak interaction (unifying the weak and electromagnetic interaction) through the symmetry group SU(3) × SU(2) × U(1). In the current epoch the strong interaction is not unified with the electroweak interaction, but from the observed running of the coupling constants it is believed they all converge to a single value at very high energies.

Phenomenology at lower energies in quantum chromodynamics is not completely understood due to the difficulties of managing such a theory with a strong coupling. This may be the reason why confinement has not been theoretically proven, though it is a consistent experimental observation. This shows why QCD confinement at low energy is a mathematical problem of great relevance, and why the Yang–Mills existence and mass gap problem is a Millennium Prize Problem.
Mathematical overview
See also: Yang-Mills equations

Yang–Mills theories are special examples of gauge theories with a non-abelian symmetry group given by the Lagrangian

\( {\mathcal {L}}_{\mathrm {gf} }=-{\frac {1}{2}}\operatorname {Tr} (F^{2})=-{\frac {1}{4}}F^{a\mu \nu }F_{\mu \nu }^{a} \)

with the generators \( \displaystyle T^{a}} \) of the Lie algebra, indexed by a, corresponding to the F-quantities (the curvature or field-strength form) satisfying
\)
\( {\displaystyle \operatorname {Tr} (T^{a}T^{b})={\frac {1}{2}}\delta ^{ab},\quad [T^{a},T^{b}]=if^{abc}T^{c}.}

Here, the fabc are structure constants of the Lie algebra (totally antisymmetric if the generators of the Lie algebra are normalised such that \( {\displaystyle Tr(T^{a}T^{b})} \) is proportional with δ\( {\displaystyle \delta ^{ab}}) \) , the covariant derivative is defined as

\( {\displaystyle D_{\mu }=I\partial _{\mu }-igT^{a}A_{\mu }^{a},} \)

I is the identity matrix (matching the size of the generators), \( A_{\mu }^{a} \) is the vector potential, and g is the coupling constant. In four dimensions, the coupling constant g is a pure number and for a SU(N) group one has \( a,b,c=1\ldots N^{2}-1 \) .

The relation

\( F_{\mu \nu }^{a}=\partial _{\mu }A_{\nu }^{a}-\partial _{\nu }A_{\mu }^{a}+gf^{abc}A_{\mu }^{b}A_{\nu }^{c} \)

can be derived by the commutator

\( [D_{\mu },D_{\nu }]=-igT^{a}F_{\mu \nu }^{a}. \)

The field has the property of being self-interacting and the equations of motion that one obtains are said to be semilinear, as nonlinearities are both with and without derivatives. This means that one can manage this theory only by perturbation theory with small nonlinearities.

Note that the transition between "upper" ("contravariant") and "lower" ("covariant") vector or tensor components is trivial for a indices (e.g. \( f^{abc}=f_{abc}) \), whereas for μ and ν it is nontrivial, corresponding e.g. to the usual Lorentz signature, \( \eta _{\mu \nu }={\rm {diag}}(+---) \).

From the given Lagrangian one can derive the equations of motion given by

\( \partial ^{\mu }F_{\mu \nu }^{a}+gf^{abc}A^{\mu b}F_{\mu \nu }^{c}=0. \)

Putting \( F_{\mu \nu }=T^{a}F_{\mu \nu }^{a} \), these can be rewritten as

\( (D^{\mu }F_{\mu \nu })^{a}=0.

A Bianchi identity holds

\( (D_{\mu }F_{\nu \kappa })^{a}+(D_{\kappa }F_{\mu \nu })^{a}+(D_{\nu }F_{\kappa \mu })^{a}=0 \)

which is equivalent to the Jacobi identity

\( [D_{\mu },[D_{\nu },D_{\kappa }]]+[D_{\kappa },[D_{\mu },D_{\nu }]]+[D_{\nu },[D_{\kappa },D_{\mu }]]=0 \)

since \( [D_{\mu },F_{\nu \kappa }^{a}]=D_{\mu }F_{\nu \kappa }^{a} \). Define the dual strength tensor \( {\tilde {F}}^{\mu \nu }={\frac {1}{2}}\varepsilon ^{\mu \nu \rho \sigma }F_{\rho \sigma } \), then the Bianchi identity can be rewritten as

\( D_{\mu }{\tilde {F}}^{\mu \nu }=0. \)

A source \( J_{\mu }^{a} \)enters into the equations of motion as

\( \partial ^{\mu }F_{\mu \nu }^{a}+gf^{abc}A^{b\mu }F_{\mu \nu }^{c}=-J_{\nu }^{a}. \)

Note that the currents must properly change under gauge group transformations.

We give here some comments about the physical dimensions of the coupling. In D dimensions, the field scales as\( [A]=[L^{\frac {2-D}{2}}] \) and so the coupling must scale as \( [g^{2}]=[L^{D-4}] \) . This implies that Yang–Mills theory is not renormalizable for dimensions greater than four. Furthermore, for D = 4, the coupling is dimensionless and both the field and the square of the coupling have the same dimensions of the field and the coupling of a massless quartic scalar field theory. So, these theories share the scale invariance at the classical level.

Quantization

A method of quantizing the Yang–Mills theory is by functional methods, i.e. path integrals. One introduces a generating functional for n-point functions as

\( Z[j]=\int [dA]\exp \left[-{\frac {i}{2}}\int d^{4}x\operatorname {Tr} (F^{\mu \nu }F_{\mu \nu })+i\int d^{4}x\,j_{\mu }^{a}(x)A^{a\mu }(x)\right], \)

but this integral has no meaning as it is because the potential vector can be arbitrarily chosen due to the gauge freedom. This problem was already known for quantum electrodynamics but here becomes more severe due to non-abelian properties of the gauge group. A way out has been given by Ludvig Faddeev and Victor Popov with the introduction of a ghost field (see Faddeev–Popov ghost) that has the property of being unphysical since, although it agrees with Fermi–Dirac statistics, it is a complex scalar field, which violates the spin–statistics theorem. So, we can write the generating functional as

\( {\begin{aligned}Z[j,{\bar {\varepsilon }},\varepsilon ]&=\int [dA][d{\bar {c}}][dc]\exp \left\{iS_{F}[\partial A,A]+iS_{gf}[\partial A]+iS_{g}[\partial c,\partial {\bar {c}},c,{\bar {c}},A]\right\}\\&\exp \left\{i\int d^{4}xj_{\mu }^{a}(x)A^{a\mu }(x)+i\int d^{4}x[{\bar {c}}^{a}(x)\varepsilon ^{a}(x)+{\bar {\varepsilon }}^{a}(x)c^{a}(x)]\right\}\end{aligned}} \)

being

\( {\displaystyle S_{F}=-{\frac {1}{2}}\int \operatorname {d} \!^{4}x\operatorname {Tr} (F^{\mu \nu }F_{\mu \nu })} \)

for the field,

\( {\displaystyle S_{gf}=-{\frac {1}{2\xi }}\int \operatorname {d} \!^{4}x(\partial \cdot A)^{2}} \)

for the gauge fixing and

\( {\displaystyle S_{g}=-\int \operatorname {d} \!^{4}x({\bar {c}}^{a}\partial _{\mu }\partial ^{\mu }c^{a}+g{\bar {c}}^{a}f^{abc}\partial _{\mu }A^{b\mu }c^{c})} \)

for the ghost. This is the expression commonly used to derive Feynman's rules (see Feynman diagram). Here we have ca for the ghost field while ξ fixes the gauge's choice for the quantization. Feynman's rules obtained from this functional are the following

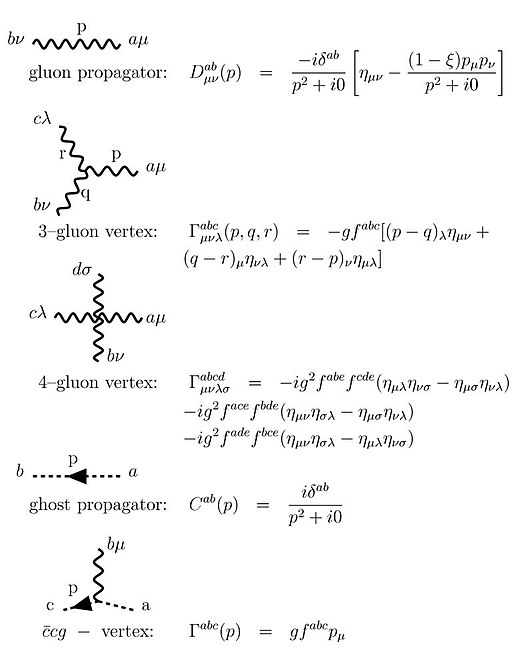
These rules for Feynman diagrams can be obtained when the generating functional given above is rewritten as

\( {\begin{aligned}Z[j,{\bar {\varepsilon }},\varepsilon ]&=\exp \left(-ig\int d^{4}x\,{\frac {\delta }{i\delta {\bar {\varepsilon }}^{a}(x)}}f^{abc}\partial _{\mu }{\frac {i\delta }{\delta j_{\mu }^{b}(x)}}{\frac {i\delta }{\delta \varepsilon ^{c}(x)}}\right)\\&\qquad \times \exp \left(-ig\int d^{4}xf^{abc}\partial _{\mu }{\frac {i\delta }{\delta j_{\nu }^{a}(x)}}{\frac {i\delta }{\delta j_{\mu }^{b}(x)}}{\frac {i\delta }{\delta j^{c\nu }(x)}}\right)\\&\qquad \qquad \times \exp \left(-i{\frac {g^{2}}{4}}\int d^{4}xf^{abc}f^{ars}{\frac {i\delta }{\delta j_{\mu }^{b}(x)}}{\frac {i\delta }{\delta j_{\nu }^{c}(x)}}{\frac {i\delta }{\delta j^{r\mu }(x)}}{\frac {i\delta }{\delta j^{s\nu }(x)}}\right)\\&\qquad \qquad \qquad \times Z_{0}[j,{\bar {\varepsilon }},\varepsilon ]\end{aligned}} \)

with

\( Z_{0}[j,{\bar {\varepsilon }},\varepsilon ]=\exp \left(-\int d^{4}xd^{4}y{\bar {\varepsilon }}^{a}(x)C^{ab}(x-y)\varepsilon ^{b}(y)\right)\exp \left({\tfrac {1}{2}}\int d^{4}xd^{4}yj_{\mu }^{a}(x)D^{ab\mu \nu }(x-y)j_{\nu }^{b}(y)\right) \)

being the generating functional of the free theory. Expanding in g and computing the functional derivatives, we are able to obtain all the n-point functions with perturbation theory. Using LSZ reduction formula we get from the n-point functions the corresponding process amplitudes, cross sections and decay rates. The theory is renormalizable and corrections are finite at any order of perturbation theory.

For quantum electrodynamics the ghost field decouples because the gauge group is abelian. This can be seen from the coupling between the gauge field and the ghost field that is \( {\bar {c}}^{a}f^{abc}\partial _{\mu }A^{b\mu }c^{c} \) . For the abelian case, all the structure constants \( f^{abc} \) are zero and so there is no coupling. In the non-abelian case, the ghost field appears as a useful way to rewrite the quantum field theory without physical consequences on the observables of the theory such as cross sections or decay rates.

One of the most important results obtained for Yang–Mills theory is asymptotic freedom. This result can be obtained by assuming that the coupling constant g is small (so small nonlinearities), as for high energies, and applying perturbation theory. The relevance of this result is due to the fact that a Yang–Mills theory that describes strong interaction and asymptotic freedom permits proper treatment of experimental results coming from deep inelastic scattering.

To obtain the behavior of the Yang–Mills theory at high energies, and so to prove asymptotic freedom, one applies perturbation theory assuming a small coupling. This is verified a posteriori in the ultraviolet limit. In the opposite limit, the infrared limit, the situation is the opposite, as the coupling is too large for perturbation theory to be reliable. Most of the difficulties that research meets is just managing the theory at low energies. That is the interesting case, being inherent to the description of hadronic matter and, more generally, to all the observed bound states of gluons and quarks and their confinement (see hadrons). The most used method to study the theory in this limit is to try to solve it on computers (see lattice gauge theory). In this case, large computational resources are needed to be sure the correct limit of infinite volume (smaller lattice spacing) is obtained. This is the limit the results must be compared with. Smaller spacing and larger coupling are not independent of each other, and larger computational resources are needed for each. As of today, the situation appears somewhat satisfactory for the hadronic spectrum and the computation of the gluon and ghost propagators, but the glueball and hybrids spectra are yet a questioned matter in view of the experimental observation of such exotic states. Indeed, the σ resonance[6][7] is not seen in any of such lattice computations and contrasting interpretations have been put forward. This is a hotly debated issue.

Open problems

Yang–Mills theories met with general acceptance in the physics community after Gerard 't Hooft, in 1972, worked out their renormalization, relying on a formulation of the problem worked out by his advisor Martinus Veltman.[8] Renormalizability is obtained even if the gauge bosons described by this theory are massive, as in the electroweak theory, provided the mass is only an "acquired" one, generated by the Higgs mechanism.

The mathematics of the Yang–Mills theory is a very active field of research, yielding e.g. invariants of differentiable structures on four-dimensional manifolds via work of Simon Donaldson. Furthermore, the field of Yang–Mills theories was included in the Clay Mathematics Institute's list of "Millennium Prize Problems". Here the prize-problem consists, especially, in a proof of the conjecture that the lowest excitations of a pure Yang–Mills theory (i.e. without matter fields) have a finite mass-gap with regard to the vacuum state. Another open problem, connected with this conjecture, is a proof of the confinement property in the presence of additional Fermion particles.

In physics the survey of Yang–Mills theories does not usually start from perturbation analysis or analytical methods, but more recently from systematic application of numerical methods to lattice gauge theories.
See also

Aharonov–Bohm effect
Coulomb gauge
Gauge covariant derivative
Kaluza–Klein theory
Lattice gauge theory
Lorenz gauge
N = 4 supersymmetric Yang–Mills theory
Propagator
Quantum gauge theory
Field theoretical formulation of the standard model
Symmetry in physics
Weyl gauge
Yang–Mills existence and mass gap
Yang–Mills equations
Yang–Mills–Higgs equations
Hermitian Yang–Mills equations
Deformed Hermitian Yang–Mills equations
Gauge theory (mathematics)

References

Straumann, N (2000). "On Pauli's invention of non-abelian Kaluza-Klein Theory in 1953". arXiv:gr-qc/0012054.
See Abraham Pais' account of this period as well as L. Susskind's "Superstrings, Physics World on the first non-abelian gauge theory" where Susskind wrote that Yang–Mills was "rediscovered" only because Pauli had chosen not to publish.
Reifler, N (2007). "Conditions for exact equivalence of Kaluza-Klein and Yang–Mills theories". arXiv:0707.3790 [gr-qc].
Yang, C. N.; Mills, R. (1954). "Conservation of Isotopic Spin and Isotopic Gauge Invariance". Physical Review. 96 (1): 191–195. Bibcode:1954PhRv...96..191Y. doi:10.1103/PhysRev.96.191.
An Anecdote by C. N. Yang
Caprini, I.; Colangelo, G.; Leutwyler, H. (2006). "Mass and width of the lowest resonance in QCD". Physical Review Letters. 96 (13): 132001. arXiv:hep-ph/0512364. Bibcode:2006PhRvL..96m2001C. doi:10.1103/PhysRevLett.96.132001. PMID 16711979. S2CID 42504317.
Yndurain, F. J.; Garcia-Martin, R.; Pelaez, J. R. (2007). "Experimental status of the ππ isoscalar S wave at low energy: f0(600) pole and scattering length". Physical Review D. 76 (7): 074034. arXiv:hep-ph/0701025. Bibcode:2007PhRvD..76g4034G. doi:10.1103/PhysRevD.76.074034. S2CID 119434312.

't Hooft, G.; Veltman, M. (1972). "Regularization and renormalization of gauge fields". Nuclear Physics B. 44 (1): 189–213. Bibcode:1972NuPhB..44..189T. doi:10.1016/0550-3213(72)90279-9. hdl:1874/4845.