Optimierungsprobleme im Antiken Griechenland

Bees were endowed with a certain geometrical forethought .... There being, then, three figures which of themselves can fill up the space round a point, viz. the triangle, the square and the hexagon, the bees have wisely selected for their structure that which contains the most angles, suspecting indeed that it could hold more honey than either of the other two. Pappus of Alexandria

Geometric Optimization

Advertisement for a modern Optimization Tool

As Geometry plays a important role in Greek Ancient Science it is not very surprising that optimization problems have been considered and solved.

In Euclid's book III of the Elements there is a discussion of the greatest and least straight lines that can be drawn from a point to the circumference of a circle, and in book VI. (in a proposition generally omitted from editions of his works) the parallelogram of greatest area with a given perimeter.

Apollonius of Perga (Απολλώνιος ο Περγαίος) investigated the greatest and least distances of a point from the perimeter of a conic section, and discovered them to be the normals, and that their feet were the intersections of the conic with a rectangular hyperbola.

Some remarkable theorems on maximum areas are attributed to Zenodorus (Ζηνόδωρος ο Γεωμέτρης), and preserved by Pappus of Alexandria (Πάππος ο Αλεξανδρεύς) and Theon of Alexandria (Θέων ο Αλεξανδρεύς):

• Of polygons of N sides with a given perimeter the regular polygon encloses the greatest area.

• Of two regular polygons of the same perimeter, that with the greater number of sides encloses the greater area.

• The circle encloses a greater area than any polygon of the same perimeter.

• The sum of the areas of two isosceles triangles on given bases, the sum of whose perimeters is given, is greatest when the triangles are similar.

• Of segments of a circle of given perimeter, the semicircle encloses the greatest area.

• The sphere is the surface of given area which encloses the greatest volume.

Maximization

Archimedes solves the problem to find the maximum of f(x) = x² (x-a) as part of the problem to divide a sphere in two parts so that the volume ratio of these parts is equal to a given ratio m/n. The solution was lost but Eutocius who wrote comments about the work of Archimedes was able to reconstruct the solution which involves the use of conic sections.(as intersection points of a hyperbola and a parabel)

Physics

W. Yourgrau and S. Mandelstam have traced the development of the variational methodology, starting with Aristotle's observation that most motion appears to be in either straight lines or circles. Aristotle suggested a common generating principle, namely minimalization:

The straight line is the shortest route between two points, while the circle is the shortest periphery for a given area.

The principle was then applied by Heron of Alexandria to prove that in a mirror, the angle of reflection is equal to the angle of incidence. Fifteen centuries later, Fermat (1601- 1665) used the same principle of the fastest route or minimal travel-time for the transition of light between two media, i.e. for the derivation of Snell's law.

A derivation of the proof is given by Judith V. Grabiner in How Looking for the Best Explanations Revealed the Properties of Light that is reproduced below:

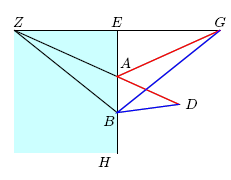
Consider AB a plane mirror, G the eye, and D the object of vision. Let a ray GA be incident upon this mirror such that \_EAG = \_BAD. Let another ray GB also be incident upon the mirror. Draw BD. I say that GA + AD < GB + BD.

Draw GE from G perpendicular to AB, and extend GE and AD until they meet, say at Z. Draw ZB. Now, we know \_BAD = \_EAG, and \_ZAE = \_BAD (as vertical angles). Therefore, \_ZAE = \_EAG. And since the angles at E are right angles, ZA = GA and ZB = GB.

But ZD < ZB + BD and ZD = ZA + AD. We deduce that GA + AD < GB + BD.

The first general method of investigating maxima and minima seems to have been published in A.D. 1629 by Pierre Fermat.

Packing

The honeycomb conjecture:

Any partition of the plane into regions of equal area has perimeter at least that of the regular hexagonal grid (i.e., the honeycomb, illustrated above). The conjecture was finally proven by Hales (1999, 2001). Pappus refers to the problem in his fifth book.

• Even way back in the time of the ancient Greeks, it was conjectured that the familiar honeycomb shape we see, which is a repeating hexagonal pattern -- they're cylinders, hexagonal-shaped cylinders, stacked one against the other in an endless array -- even in the times of the ancient Greeks it was conjectured, I think it was Pappus in fact who conjectured that that was the most efficient way of storing honey -- efficient in the sense of it uses the minimum amount of wax to store a certain volume of honey. Dr. Keith Devlin about what's known as "the honeycomb conjecture"

• In Book V Pappus takes up a topic not mentioned by Euclid, but apparently discussed by the Athenian mathematician Zenodorus.... This topic is the isoperimetric problem: Which plane figure of a given perimeter encloses the largest area? Which solid figure having a given surface area encloses the largest volume? Pappus introduces this problem with one of the most charming essays in the history of mathematics, one that has frequently been excerpted under the title On the Sagacity of Bees. Pappus speaks poetically of the divine mission of the bees to bring from heaven the wonderful nectar known as honey, and says that in keeping with this mission they must make their honeycombs without any cracks through which honey could be lost. Having also a divine sense of symmetry, the bees had to choose among the regular shapes that could fulfill this condition, that is, triangles, squares, and hexagons. They chose the hexagon because a hexagonal prism required the least material to enclose a given volume. Roger Cooke, The History of Mathematics, A Brief Course, John Wiley and Sons.

• Book V [of Pappus] is largely devoted to isoperimetry, or the comparison of the areas of figures having equal bounding perimeters and of volumes of solids having equal bounding areas. This book also contains an interesting passage on bees and the maximum-minimum properties of the cells of their honeycombs. Howard Eves, An Introduction to the History of Mathematics.

• The Pappus Problem. Book V of the Collection was a favorite with later commentators, for it raised the question of the sagacity of bees. Inasmuch as Pappus showed that of two regular polygons having equal perimeters the one with the greater number of sides has the greater area, he concluded that bees demonstrated some degree of mathematical understanding in constructing their cells as hexagonal, rather than square or triangular prisms. The book goes into other problems of isoperimetry, including a demonstration that the circle has a greater area, for given perimeter, than does any regular polygon. Here Pappus seems to have been following closely a work On Isometric Figures written almost half a millenium earlier by Zenodorus (ca. 180 B.C.), some fragments of which were preserved by later commentators. Carl B. Boyer, A History of Mathematics, Second Edition, John Wiley and Sons.

• Zenodorus wrote, at some date between (say 200 B.C. and A.D. 90, a treatise ... On isometric figures. A number of propositions from it are preserved in the commentary of Theon of Alexandria on Book I of Ptolemy's Syntaxis; and they are reproduced in Latin in the third volume of Hultsch's edition of Pappus, for the purpose of comparison with Pappus's own exposition of the same propositions at the beginning of his Book V, where he appears to have followed Zenodorus pretty closely while making some changes in detail. A History of Greek Mathematics, Sir Thomas Heath, Oxford, 1921.

• Book V. Preface on the Sagacity of Bees. It is characteristic of the great Greek mathematicians that, whenever they were free from the restraint of the technical language of mathematics, as when for instance they had occasion to write a preface, they were able to write in language of the highest literary quality, comparable with that of the philosophers, historians, and poets. We have only to recall the introductions to Archimedes's treatises and the prefaces to the different Books of Apollonius's Conics. Heron, though severely practical, is not exception when he has any general explanation, historical or other, to give. We have now to note a like case in Pappus, namely the preface to Book V of the Collection. The editor, Hultsch, draws attention to the elegance and purity of the language and the careful writing; the latter is illustrated by the studied avoidance of hiatus. The subject is one which a writer of taste and imagination would naturally find attractive, namely the practical intelligence shown by bees in selecting the hexagonal form for the cells in the honeycomb. Pappus does not disappoint us; the passage is as attractive as the subject, and deserves to be reproduced.

• `It is of course to men that God has given the best and the most perfect notion of wisdom in general and of mathematical science in particular, but a partial share in these things he allotted to some of the unreasoning animals as well. To men, as being endowed with reason, he vouchsafed that they should do everything in the light of reason and demonstration, but to the other animals, while denying them reason, he granted that each of them should, by virtue of a certain natural instinct, obtain just so much as is needful to support life. This instinct may be observed to exist in the very many other species of living creatures, but most of all in bees. In the first place their orderliness and their submission to the queens who rule in their state are truly admirable, but much more admirable still their emulation, the cleanliness they observe in the gathering of honey, and the forethought and housewifely care they devote to its custody. Presumably because they know themselves to be entrusted with the task of bringing from the gods to the accomplished portion of mankind a share of ambrosia in this form, they do not think it proper to pour it carelessly on ground or wood or any other ugly and irregular material; but, first collecting the sweets of the most beautiful flowers which grow on earth, they make from them, for the reception of the honey, the vessels which we call honeycombs, (with cells) all equal, similar and contiguous to one another, and hexagonal in form. And that they have contrived this by virtue of a certain geometrical forethought we may infer in this way. They would necessarily think that the figures must be such as to be contiguous to one another, that is to say, to have their sides common, in order that no foreign material could enter the interstices between them and so defile the purity of their produce. Now only three rectilineal figures would satisfy the condition, I mean regular figures which are equilateral and equiangular; for the bees would have none of the figures which are not uniform... There being then three figures capable by themselves of exactly filling up the space about the same point, the bees by reason of their instinctive wisdom chose for the construction of the honeycomb the figure which has the most angles because they conceived that it would contain more honey than either of the two others...`Bees then, know just this face which is of service to themselves, that the hexagon is greater than the square and the triangle and will hold more honey for the same expenditure of material used in constructing the different figures. We, however, claiming as we do a greater share in wisdom than bees, will investigate a problem of still wider extent, namely that, of all equilateral and equiangular plane figures having an equal perimeter, that which has the greater number of angles is always greater, and the greatest plane figure of all those which have a perimeter equal to that of the polygon is the circle.' Sir Thomas Heath, A History of Greek Mathematics, Oxford, 1921.

• Chapter I The beginnings of geometry. The subject of geometry, whether we consider it as a science or an art, has a very long history.... What is the earliest example of purposive geometrical construction.... If a pigeon fly straight rather than on a curve, once it has decided the direction of its home, we are safe in saying that it has intentionally taken the shortest path and applaud its sagacity, without inquiring as to whether the real reason was not that it had an impulse to go straight, and none to bend.... Another example in Nature where great credit has been given for geometrical sagacity is found in the cell-structure of the honey bee. Such a cell is a prism whose section is approximately a regular hexagon, while the ends are three-faced `steeples'. The cleverness of the creature in constructing a habitation of hexagonal section excited the admiration of Pappus, some sixteen hundred years ago: [Heath's translation of Pappus is quoted here.] But the bee's skill in solving problems in maxima and minima does not end here. It was found on examination that the angle formed by the faces of the steeple with the axis was such as to make the total surface for a given volume a minimum, a result experimentally determined by MacLaurin. What clever bees! But were the really so clever? Let us look at the matter more closely.... Julian Coolidge, A History of Geometrical Methods, Dover.

• Much has been written on the this question of the geometry of the honeycomb. The bee's strange social habits and geometric talents could not fail to attract the attention and excite the admiration of their human observers and exploiters. ``My house,'' says the bee in the Arabian Nights, ``is constructed according to the laws of a most severe architecture; and Euclid himself could learn from studying the geometry of my cells.''..Darwin ... spoke of the bees' architecture as ``the most wonderful of known instincts'' and adds: ``Beyond this stage of perfection in architecture natural section (which has replace divine guidance!) could not lead; for the comb of the hive-bee, as far as we can see, is absolutely perfect in economizing labor and wax.'' Weyl, Symmetry, 1952.

What Jeremy Taylor called ``the discipline of bees and the rare fabric of honeycombs'' must have attracted the attention and excited the admiration of mathematicians from time immemorial. ``Ma maison est construite,'' says the bee in the Arabian Nights, ``selon les lois d'une sévère architecture; et Euclidos lui-même s'instruirait en admirant la géométrie de ses avéoles.'' Ausonius speaks of the geometrica forma favorum, and Pliny tells of men who gave a lifetime to its study...Pappus the Alexandrine has left us an account of its hexagonal plan, and drew from it the conclusion that the bees were endowed with ``a certain geometrical forethought''. ``There being, then, three figures which of themselves can fill up the space round a point, viz. the triangle, the square and the hexagon, the bees have wisely selected for their structure that which contains the most angles, suspecting indeed that it could hold more honey than either of the other two.'' [footnote: This was according to the ``theorem of Zenodorus.'' The use by Pappus of ``economy'' as a guiding principle is remarkable. For it means that, like Hero with his mirrors, he had a pretty clear adumbration of that principle of minima which culminated in the principle of least action, which guided eighteenth-century physics, was generalised (after Fermat) by Lagrange, inspired Hamilton and Maxwell, and reappears in the latest developments of wave-mechanics.] Thompson, On Growth and Form

Life Optimization

According to Aristotle in his Nicomachen Ethics choose the mean between the extremes : Book II - Virtue, Moderation and the Mean

Quotations:

Olympiodorus, 6th century: “nature does nothing superfluous or any unnecessary work.”, later a similar statement in Occam's razor principle, William Occam, 14th century: “the simplest explanations are the best.”

Sources

Hales, T. C. "The Hexagonal Honeycomb Conjecture." http://www.math.pitt.edu/~thales/kepler98/honey/

Hales, T. C. "Background on the Hexagonal Honeycomb Conjecture." http://www.math.pitt.edu/~thales/kepler98/honey/hexagonHistory.html

Yourgrou, W. and Mandelstam, S., Variational Principles in Dynamics and Quantum Theory, Dover Pub., New York (1968), 201 pp.

Judith V. Grabiner, How Looking for the Best Explanations Revealed the Properties of Light.

LINKS

A Historical Review of the Isoperimetric Theorem in 2-D, and its place in Elementary Plane Geometry (PDF File)

Geometric Mean and Arithmetic Mean (A Greek Geometric Problem)

The cell of a honeycomb