.
Geometry has two great treasures: one is the Theorem of Pythagoras; the other, the division of a line into extreme and mean ratio. The first we may compare to a measure of gold; the second we may name a precious jewel.
Johannes Kepler, (1571-1630)
Euclid in Book 6, Proposition 30 shows how to divide a line in mean and extreme ratio which we would call "finding the golden section G point on the line". Euclid used this phrase to mean the ratio of the smaller part of this line, GB to the larger part AG (ie the ratio GB/AG) is the SAME as the ratio of the larger part, AG, to the whole line AB (ie is the same as the ratio AG/AB).
![]()
AB/AG = AG/GB. If AB = 1 and AG = x then GB = 1-x and 1/x = x/(1-x) and it follows x2 = 1-x, i.e. x2 + x - 1 = 0
The golden section was found by the Pythagoreans who used the Pentagram formed, by the diagonals of a regular Pentagon, as a symbol of their school. It was probably known much earlier in Egypt as some ratio of lengths and heights of Pyramids suggest. Pythagoras may have obtained this knowledge when he visited Egypt. Theano of Thurii (Θεανώ) c. 500 BC, the wife of Pythagoras is assumed to have written a book Theorem of the golden mean.
The name Golden section probably is due to Martin Ohm from his Mathematics book (1835) (in German “Der Goldene Schnitt” ) maybe chosen due to the comment of Kepler. There are some who say that Leonardo da Vinci (1452 – 1519) used the name sectio aurea for the golden section even much earlier but this name was not used by others.
The golden rectangle R, constructed by the Greeks, has the property that when a square is removed a smaller rectangle of the same shape remains. Thus a smaller square can be removed, and so on, with a spiral pattern resulting. The sides are in the "golden proportion" (1 : 1.618034 which is the same as 0.618034 : 1) has been known since it occurs naturally in some of the proportions of the Five Platonic Solids
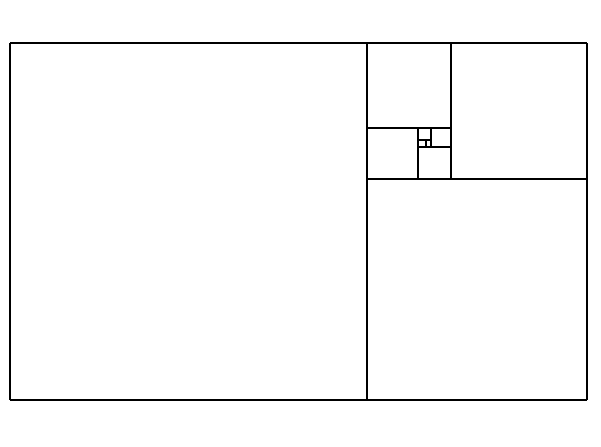
Note that the golden Rectangle can be approximated by adding squares like a spiral with a edge length: 1, 1, 2, 3, 5, 8, 13, 21, 34...the Fibonacci numbers that approach the golden ratio always better if we consider the value of the ratios 1/1, 2/1, 3/2, 5/3, 8/5, 13/8, 21/13, 34/21,...
The Greeks were thus able to see geometrically that the sides of R have an irrational ratio, 1 : x. The smaller rectangle has sides with ratio 1-x : 1; since this is the same as the ratio for the big rectangle, one finds that x2 = x+1 and thus x = (1+sqrt(5))/2 = 1.618033989.... (where sqrt(5) is the square root of 5). For the number 1.61803389.. often the Greek symbol phi is used (due to Mark Barr since 1909 used this symbol as the initial of Pheidias, the Greek sculptor, who is supposed to have used this in the Parthenon ( Livio 2002)

The Pentagon, and the Pythagoras Pentagram Symbol , The symbol of the Golden Section Phi (derived from Pheidias), Plato's Dodecahedron, Archimedes Pi, the Vitruvius Man...
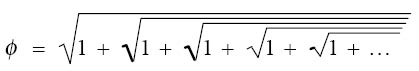
One of many interesting ways of how phi can be expressed.
.
A stamp with a series of 7 golden rectangles and a logarithmic spiral (Scott 805, Michel 1337).
Spirals and the Golden Section , Animation Golden Rectangle and Fibonacci numbers
The golden rectangle was considered by the Greeks to be of the most pleasing proportions, and it was used in ancient architecture.
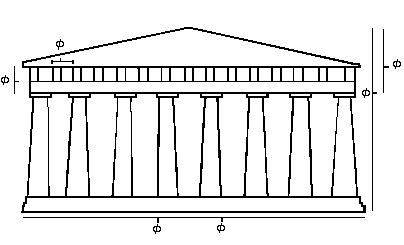
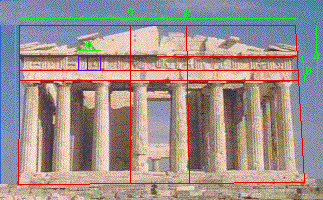
In some modern buildings such as of Le Corbusier (a Swiss architect born as Charles-Edouard Jeanneret-Gris, 1887-1965) the Golden Section is used and this is also assumed for the Parthenon as the images suggest. But is this true? For the dimensions of the Parthenon I have the following numbers: W = 30.88 m , L = 69.5 m and H = 13.72 m. With r = 9/4 this satisfies approximately the following relations : r*H = W, r*W = L and therefore also r2*H = L and therefore more likely the golden section rule is not applied for the Pathenon. For other Greek temples such as the Poseidon temple in Paestum, which is older than the Parthenon, the use of the golden section is assumed, see the image, but why the points shown have been selected, such as one on the third left column?
(The Parthenon is a relatively small Temple (The Zeus Temple of Agrigent was much larger; L = 110 m, W= 55 m)
A New Solution for the Parthenon's Golden Mean
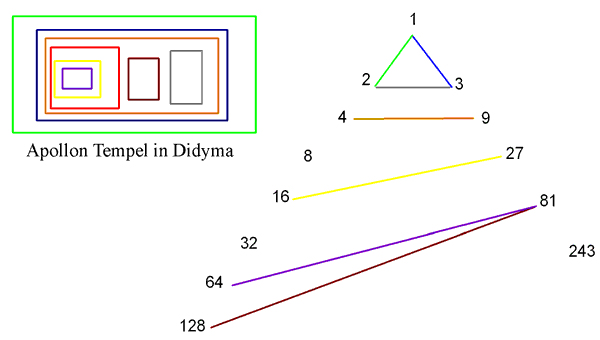
Apollo Temple in Didyma, the size of various elements are expressed by ratios of integer numbers from Platonic Pythagorean ideas
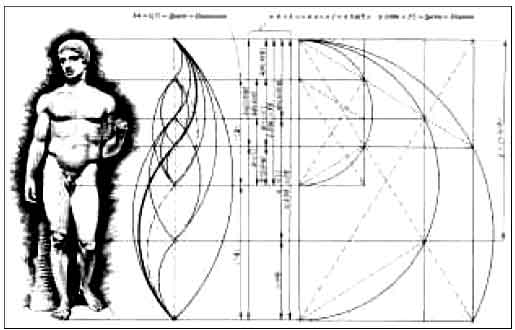
The Doryphoros is assumed to be also described by the Golden Proportion characteristic numbers, according for example to Gyorgy Doczi, The Power of Limits: Proportional Harmonies in Nature, Art and Architecture
Was the Golden Proportion used in Greek Theaters?
I have the following information ( Source ) :
Epidaurus Theater: The place for the spectators was divided into two tiers: the first one had 34 rows of places, the second one 21. The angle between theatron and scene divides a circumference of the basis of an amphitheater in ratio: 137°,5 : 222°,5 = 0.618.
Dionysus Theater Athens: Three tiers. The first tier has 13 sectors, the second one 21 sectors.
Now 13, 21 and 34 are Fibonacci numbers (0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, ...) with the property that the ratio an+1/an converges to phi.
Le Corbusier, one of the most important architects of the 20th century, was also interested in how the golden ratio is related to the anatomy of the human body. The United Nations building is divided in 3 golden rectangles but if you ask me it looks not very nice!

Le Corbusier building Paris/France
Leon Battista Alberti (1404–1472), a Florentine painter, sculptor, architect, musician, and poet ,or as he used to say a universal man, defined as a composition that rule by which the parts of things fit together. The golden rectangle rule was an important such harmonious proportion of parts in Art.

There was yet a fifth combination which God used in the delineation of the universe with figures of animals.
Plato: Timaeus (54b-55c) p 1180
Plato says this discussing the dodecahedron. Maybe some explanation for this is that the pentagon is associated with the golden section and the corresponding ratio is observed in various biological systems (see the Links).
One must be careful if the use of the golden section in Art and Architecture as assumed by the Greeks in the Parthenon or elsewhere is actually true! The images may suggest that the Golden rectangle can be found in various parts. The golden rectangle is probably the most aesthetic rectangle at least as some tests have shown the result was close to the golden rectangle among different rectangles. It is this reason that probably many approximations of the golden rectangle can be found in various other examples in Art and Architecture.
Critical comments about the golden section from the American Mathematical Society
Nevertheless there are some very important mathematical properties of the golden section. These properties are used in optimization algorithms such as the golden ratio search. It is incredible but the golden ratio number 1.618... is the most irrational among all irrational numbers: The most irrational number (American Mathematical Society)
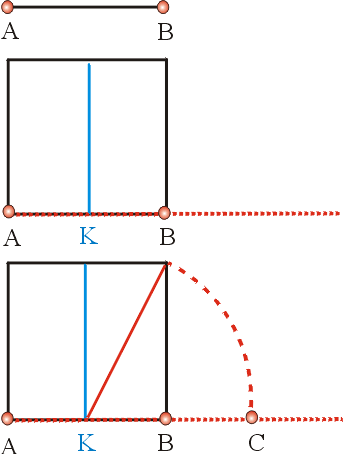
Construction of the Golden Section and the Golden Rectangle, given AB the smaller side of the golden rectangle. Take a square with side AB and a perpendicular at the center of AB at K (AK = KB). Take the radius KB and draw a circle with K as center. The extension of AB is intersected at C. AC is the larger side of the golden rectangle.
See also: Kurt Hofstetter, A 5-step Division of a Segment in the Golden Section. Forum Geometricorum Volume 3 (2003) 205–206. (PDF File)
The Golden Section and the Fibonacci numbers in Nature
Twig and Leaf Phyllotaxy (Phyllotaxy from the Greek words phyllon, “leaf” and taxis, “arrangement”, arrangement of leaves on the stems of plants) about the golden section in Nature
Fibonacci Numbers in Nature
Fibonacci phyllotaxis: Turing's problem
Mathematics in the natural world (PDF File, c. 800 KB)
Anatomy
What has the golden ratio to do with beauty or anatomy ?
http://www.beautyanalysis.com/index2_mba.htm
The golden ratio can be found also in the “molecule of life”, the DNA:
http://www.brooksdesign-cg.com/Code/Html/godna2.htm
Music

Henri Christiné (1867 - 1941). Phi-Phi.
QUOTATIONS
Now in every work of art the basis of its composition is geometry or in other words the means of determining the mutual relationship of its component parts either on plane or in space... And again, since it is mathematics which lends significance to these relationships, it is only a natural step from having perceived them to desiring to portray them. This, in brief, is the genesis of a work of art. M. Bill. The Mathematical Way of Thinking in the Visual Art of Our Time, The Visual Mind: Art and Mathematics, M. Emmer, editor, Leonardo Books-MIT Press, Cambridge, 1993.
Mathematics
Golden Section and Mathematics
The Golden Section, from a Perseus Greek Science Course
1.618.. is the magic number. The golden rule , in Arts, Biology and Black Hole Physics a newspaper report
The Golden Ratio and the Fibonacci Numbers
Quantum Physics and the Golden Section: Hardy's test of quantum mechanics (PDF File )
Architecture and Golden Ratio
A New Solution for the Parthenon's Golden Mean ( The Parthenon )
Marcus Frings, "The Golden Section in Architectural Theory", Nexus Network Journal, vol. 4, no. 1 (Winter 2002), http://www.nexusjournal.com/Frings.html
Systems of Proportion in Design and Architecture and their Relationship to Dynamical Systems Theory
Gestalt Principles and Dynamic Symmetry Nature's Design Connections to Our Built World
TOOLS
How to get the divine proportion instantly into your composition; Plugin from PowerRetouche.com
Martin Ohm, M. die Reine Elementar-Mathematik., 2nd edition, Berlin: Jonas Veilags-Buchhandlung, 1835.
The Golden Ratio: The Story of Phi, the World's Most Astonishing Number , Livio, M. The Golden Ratio: New York: Broadway Books, 2002.
Greek Reports
Οι υπέροχοι και μυστήριοι αριθμοί Fibonacci
| Ancient Greece
Science, Technology , Medicine , Warfare, , Biographies , Life , Cities/Places/Maps , Arts , Literature , Philosophy ,Olympics, Mythology , History , Images Medieval Greece / Byzantine Empire Science, Technology, Arts, , Warfare , Literature, Biographies, Icons, History Modern Greece Cities, Islands, Regions, Fauna/Flora ,Biographies , History , Warfare, Science/Technology, Literature, Music , Arts , Film/Actors , Sport , Fashion --- |

