.

Griechische Mathematik: Zahlentheorie und Primzahlen

Pythagoras of Samos ( Πυθαγόρας ο Σάμιος) discovered the relation between harmony and numbers. The Pythagoreans saw the number one as the primordial unity from which all else is created. Two was the symbol for the female, three for the male and therefore five (two + three) symbolized marriage. The number four was symbolic of harmony, because two is even, so four (two times two) is "evenly even". Four symbolized the four elements out of which everything in the universe was made (earth, air, fire, and water). Ten that was the sum from one to four was a very special number.

The ancient Greeks believed that all numbers had to be rational numbers. 2500 years ago Greeks discovered that if all the common prime numbers were removed from the top and bottom of the ratio then one of the two numbers had to be odd. This we can term reduced form. Obviously, if top and bottom were both even, then both could be divide by the number two and this could be eliminated from both.

The Greeks then went on to show that for a right triangle with sides [1:1:square root of two] that the hypotenuse of the triangle, the square root of two, in reduced form could not have either top or bottom number odd. Consequently, it cannot be a rational number. The proof was so powerful that it caused a crisis to the Pythagorean theory of numbers.

Geometry was one of the most important research field of ancient Greeks. Even having a ugly system to represent numbers it is remarkably that they developed the basis of number theory. Gauss famously described Mathematics as the "Queen of the Sciences" and Number Theory as the "Queen of Mathematics". Prime number research is today very active both from a theoretical and experimental point. Computers spent many hours either calculating more digits of PI or trying to find larger Prime numbers, Twins, Mersenne and other special numbers.

Ancient Greeks discovered the prime numbers or πρώτοι αριθμοί (protoi arithmoi), produced some conjectures some of them still not be able to proof.

A positive integer p is called prime if 1 and p itself are its only divisors; for example, 2, 3, and 23 are prime, whereas 4 = 2 · 2 and 243 = 3 · 3 · 3 · 3· 3 are not.

Humanity has probably been fascinated by numbers since the discovery of counting. The ancient Greeks established it as a subject: Books 7-10 of Euclid's Elements are devoted to number theory. These books contain a treatment of the Euclidean algorithm, a proof that there are infinitely many primes, a theory of incommensurable (or irrationals -- the original proof that the square root of 2 is irrational is attributed to Pythagoras).

Prime Numbers

It will be millions of years before we'll have any understanding, and even then it won't be a complete understanding, because we're up against the infinite. P. Erdös, about prime numbers in Atlantic Monthly, Nov. 1987, p. 74

...there is no apparent reason why one number is prime and another not. To the contrary, upon looking at these numbers one has the feeling of being in the presence of one of the inexplicable secrets of creation. D. Zagier, The first 50 million prime numbers", The Mathematical Intelligencer (1977) 7-19.

The ancient Greeks provided a proof around 300 BC that there were infinitely many primes and that they were irregularly spaced (there can be arbitrarily large gaps between successive primes). Was this not another crisis to find that the primes did show a chaotic behavior appearing randomly distributed? Randomness as described by Chaitin could be not a problem to ancient Greeks and Romans: “ in fact they made their Gods play dice quite literally, by throwing dice in their temples, to see the will of Gods; the Emperor Claudius even wrote a book on the art of winning at dice. However, from the point of view of Christianity, playing dice with God was definitely a pagan practice -- it violates the first commandment. St. Augustine is reported to say that nothing happens by chance, because everything is controlled by the will of God.”

The ancient Greeks knew that every positive integer has a prime factorization: if n is a positive integer, then there are prime numbers p₁, . . . , p_k such that n = p₁ · · · p_k. For small n, such a prime factorization is easy to find: 6 = 2 · 3, 243 = 2 · 3 · 3 · 3 · 3, and 6785 = 5 · 23 · 59, for example. There is essentially only one way of finding a prime factorization —trying.

Thymaridas (Θυμαρίδας ο Πάριος) a Pythagorean a number theorist called a prime number rectilinear since it can only be represented one-dimensionally, whereas non-prime numbers such as 6 can be represented by rectangles of sides 2 and 3. He is known also for his epanthema (flower of Thymaridas)

For large numbers such as 7380563434803675764348389657688547618099807 the theorem tells us that it has a prime factorization. It is easy to write a little program that produces the prime factorization for this number and for any arbitrary large integer. However, the average time such a program would take to find the prime factorization of an integer n goes up dramatically as n gets large: for sufficiently large n, even the fastest super-computer available today would —on average—take longer to find the prime factorization of n than the age of the universe. So, although a prime factorization of a positive integer always exists, it may be impossibly hard to find. In fact, this is a good thing—it is at the heart of the public key codes that make credit card transactions on the Internet safe.

Euclid's Algorithm

Euclid of Alexandria (Ευκλείδης ο Αλεξανδρεύς) provided the first algorithm for the calculation of the greatest common divisor gcd(a,b) of two integers a and b. This algorithm belongs to the so called class of integer relation algorithms which for a given set of real numbers (x₁,x₂,...,x_n) try to find if integers a₁, a₂, ..., a_n (not all 0) exists such that:

a₁x₁ + a₂x₂ + ...+a_nx_n = 0.

Details about Euclid's algorithm

Sieve of Eratosthenes (κόσκινο του Ερατοσθένη)

Ancient Greek Sieve

The ancient Greek mathematician Eratosthenes Ερατοσθένης ο Κυρηναίος() (c. 276 BC Cyrene – c. 194 BC Alexandria )-who was also first to calculate the earth's correct circumference - proposed a mechanical sieve to filter prime numbers by sorting out all multiples of those numbers that were not themselves multiples of other numbers. Thus he kept 2 but threw out 4, 6, 8, etc. His sieve then kept 3 and rejected 6, 9, 12, etc. This method is very efficient for numbers of up to 1000000.

Remark: Greeks used a Sieve as Aristophanes explains in The Clouds 420 BC:

SOCRATES Zeus! what Zeus! Are you mad? There is no Zeus.
STREPSIADES What are you saying now? Who causes the rain to fall? Answer me that!
SOCRATES Why, these, and I will prove it. Have you ever seen it raining without clouds? Let Zeus then cause rain with a clear sky and without their presence!
STREPSIADES By Apollo! that is powerfully argued! For my own part, I always thought it was Zeus pissing into a sieve. But tell me, who is it makes the thunder, which I so much dread?

Sieve of Eratosthenes (PDF) (from http://www.larouchepub.com/)

Perfect Numbers

Six is a number perfect in itself, and not because God created the world in six days; rather the contrary is true. God created the world in six days because this number is perfect, and it would remain perfect, even if the work of the six days did not exist.
St. Augustine (354-430) in The City of God, who according to Bernal (1965) was "turning from wicked learning to holy nonsense.." Numerology in the Bible: "Bring some of the fish you've just caught," Jesus said. So Simon Peter went aboard and dragged the net to the shore. There were 153 large fish, and yet the net hadn't torn. 153: The Number of the Fish (Info from a machine translated Italian Website)

The Pythagoreans were fascinated by whole numbers. They defined as perfect numbers those equal to the sum of their parts (or proper divisors, including 1). For example, 6 is the smallest perfect number--the sum of its three proper divisors: 1, 2, and 3. The next perfect number is 28, which is the sum of 1, 2, 4, 7, and 14.

If as many numbers as we please beginning from a unit be set out continuously in double proportion, until the sum of all becomes prime, and if the sum multiplied into the last make some number, the product will be perfect. Euclid Elements Book IX , proposition 36

The first four perfect numbers are: 6, 28, 496, 8128. Euclid was able to find that each of these numbers is of the form 2ⁿ(2ⁿ⁺¹- 1), where 2ⁿ⁺¹-1 is prime. Euclid proved that all numbers of this form were perfect. The Pythagoreans knew that 1 + 2 + 4 + ... + 2^k = 2^k+1 - 1.

Euclid's perfect numbers are triangular.

For any positive integer n let s(n) denote the sum of those divisors. The ancient Greeks classified each natural number n as deficient, abundant, or perfect according to whether s(n) was less than, greater than, or equal to 2n.

Nicomachus of Gerasa (c. 60- c. 120 AD) provides also a list of properties of perfect numbers without a proof:

The nth perfect number has n digits.
There are infinitely many perfect numbers.
All perfect numbers are even.
All perfect numbers end in 6 and 8 alternately.

It was Euler who finally proved the converse of the above statement: that any even perfect number is of the form 2^n-1(2ⁿ-1). The difficulty of this problem is demonstrated in the fact that even Fermat himself failed to prove it. It has been conjectured, in fact, that all perfects are of the aforementioned form, which is equivalent to saying that there are no odd perfect numbers. No proof is known even today

Moreover, as the foot is the sixth part of a man’s height, they contend, that this number, namely six, the number of feet in height, is perfect: the cubit, also, being six palms, consequently consists of twenty-four digits. Hence the states of Greece appear to have divided the drachma, like the cubit, that is into six parts, which were small equal sized pieces of brass, similar to the asses, which they called oboli; and, in imitation of the twenty-four digits, they divided the obolus into four parts, which some call dichalca, others trichalca. Vitruvius, de Architectura

For more information See: Perfect Numbers

Amicable Numbers (Philoi Arithmoi)

A friend is an alter ego: Pythagoras response to the question who is a friend

The Pythagoreans were interested in what we now call amicable numbers, pairs in which each number is the sum of the proper divisors of the other. The smallest such pair is 220 and 284. The number 220 is evenly divisible by 1, 2, 4, 5, 10, 11, 20, 22, 44, 55, and 110, which add up to 284; and 284 is evenly divisible by 1, 2, 4, 71, and 142, which add up to 220. Tymicha [Tumi/xa ] (Τυμίχα η Σπαρτιάτις) c. 600 BC the wife of Milias of Crotona. A Pythagorean, according to Iamblichus one work refers to her and „amicable“ numbers.

The Pythagoreans regarded 220 and 284 as numerical symbols of friendship. For a long period of time, this was the only known pair, until the Arabic mathematician ibn al-Banna found the next pair 17296 and 18416. Fermat later rediscovered this pair, and then Rene Descartes the pair 9363584 and 9437056. Euler discovered using ingenious algorithms new amicable pairs. Today mathematicians know more than 1 million amicable pairs. "It still hasn't been proved that the number of amicable pairs is infinite," says Jan Munch Pedersen of Vejle Business College in Denmark, who maintains a database listing all known pairs. "However, the explosive growth of pairs in the last few years leaves no doubt that this conjecture is true," he adds.

Comments:

"The Pythagorean brotherhood regarded 220 and 284 as symbols of friendship. Biblical commentators spotted 220 in Genesis 32:14 as the number of goats given Esau by Jacob. A wise choice, the commentators said, because 220, being one of the amicable pair, expressed Jacob's great love for Esau. During the Middle Ages this pair of numbers played a role in horoscope casting, and talismans inscribed with 220 and 284 were believed to promote love. One poor Arab of the eleventh century recorded that he once tested erotic effect *eating* something labeled with 284, at the same time having someone else swallow 220, but he failed to add how the experiment worked out." Martin Gardner, Mathematical Magic Show. Viking, London 1984, p. 167

Diophantus, Diophantine Equations

We know almost nothing about Diophantus of Alexandria (Διόφαντος ο Αλεξανδρεύς), except that he lived, in Alexandria. He produced the first book on algebra. Our only certain knowledge of Diophantus rests upon the fact that he quotes Hypsicles (Υψικλής ο Αλεξανδρεύς)(150 BC) and that he is quoted by Theon Alexandrinus whose date is fixed by the solar eclipse of 16^th June 364 AD. Diophantus’ work was lost with the burning of the Library of Alexandria. More than a thousand years later, in 1570, six of its twelve books were found in a library in Germany. Diophantus began the systematic study of equations with integer coefficients. He was a pioneer in solving certain indeterminate algebraic equations, i.e., an equation in which the variables can take on integer values and has an infinite but denumerable set of solutions: e.g., x+2y=3.

Diophantus noticed that numbers of the form 4n + 3 cannot be the sum of two squares and 24n + 7 cannot be the sum of three squares. It is suggested that he know that every number can be written as the sum of 4 squares, but it is unlikely to have known a proof as Langrange provided much later. From Fragments of his lost book On polygonal numbers we know a few lemmata such as that given any numbers a, b then there exist numbers c, d such that a³ - b³ = c³ + d³.

Fibonacci Numbers

Did the ancient Greeks new the Fibonacci numbers? Euclid in Book 6, Proposition 30 shows how to divide a line in mean and extreme ratio which we would call "finding the golden section G point on the line". I have no direct information of a text by the ancient Greeks which discusses the Fibonacci numbers but I found the following information interesting ( Source ) :

Epidaurus Theater: The place for the spectators was divided into two tiers: the first one had 34 rows of places, the second one 21. The angle between theatron and scene divides a circumference of the basis of an amphitheater in ratio: 137°,5 : 222°,5 = 0.618.

Dionysus Theater Athens: Three tiers. The first tier has 13 sectors, the second one 21 sectors.

Now 13, 21 and 34 are Fibonacci numbers (0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, ...) with the property that the ratio a_n+1/a_n converges to phi.

Fermat's Theorem

The Pythagoreans knew solutions of the equation x²+y²=z², where x,y,z are positive integer numbers. One such example with x=3, y=4, z=5 was known much earlier in other cultures also. But the discovery of the irrational numbers was important to consider which combinations of (x,y) provide integer z values. There was no reason from geometrical considerations probably to consider equations of the form x³ + y³ = z³. One had to wait until Fermat considered this problem and without knowing the implication claimed that he has a proof but only not enough space in a book to provide it. He said that the equation xⁿ+yⁿ=zⁿ has no integer positive solutions for n greater or equal 3. The history is very well known and many mathematicians and not-mathematicians were fascinated by a simple problem to understood but without any solution provided by the greatest mathematicians over centuries. Only in 1994 Wiles provided the proof using the most advanced techniques of mathematics. It seems unlikely that ancient Greeks or Fermat could be able to provide a solution of this problem

Other number relations found by the Greeks:

The sums of the uneven numbers, as reported by Aristotle in Metaphysics, give us the series of squared numbers:

1 + 3 = 2², 1 + 3 + 5 = 3², 1 + 3 + 5 + 7 = 4², etc.

According to Plutarch the square of the n^th triangular number equals the sum of the first n cubes.

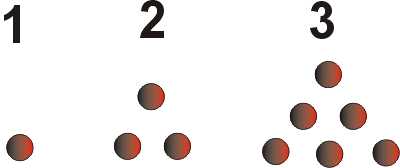
The image shows the first 3 triangular elements with 1,3 and 6 elements and their square are 1, 9 and 36 respectively. We have:

1² = 1³, 3² = 1³ + 2³, 6² = 1³+2³+3³ , etc.

This is equivalent to say that 1³+2³+...+ n³ = (n(n+1)/2)²

(More information will follow soon!)

Ancient Greeks: Prime Numbers and Number Theory

Michael Lahanas

Αρχαίοι 'Ελληνες : πρώτοι αριθμοί, θεωρία αριθμών

.