.

Griechische Mathematik: Hippokrates Quadratur

For false diagrams of geometrical figures are not contentious (for the resulting fallacies conform to the subject of the art)-any more than is any false diagram that may be offered in proof of a truth-e.g. Hippocrates’ figure or the squaring of the circle by means of the lunules. But Bryson’s method of squaring the circle, even if the circle is thereby squared, is still sophistical because it does not conform to the subject in hand. Aristotle : On Sophistical Refutations

Hippocrates of Chios (Ιπποκράτης ο Χίος) (c. 470- c. 410 BC), actually a owner of ships, while he was visiting Athens he had some discussions with mathematicians and philosophers and from these discussions he converted to a mathematician.

It is believed that Greeks knew a method for reducing a convex polygon of any number of sides to a triangle of equal area. In the figure below we consider a polygon ABCFGHJ. We take a side CF extended to meet a line GK from an adjacent vertex, running parallel to the diagonal FH in the polygon. We cut a corner by connecting H with K, while maintaining the same area. So we see a complex figure equated to a simpler one. The polygon with 7 vectices ABCFGHJ has the same area as the polygon with 6 vertices ABCKHJ.

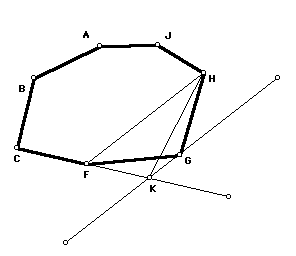
$Graphic1$

To see this we construct a parallel to FH at G. Extend CF that meets this parallel at K. FHK and FGH have the same height and base FH. A similar process can be continued with the polygon ABCKHJ again until we obtain a triangle.

Now can we “square” the final triangle? Can we produce a square with the same area as the triangle?

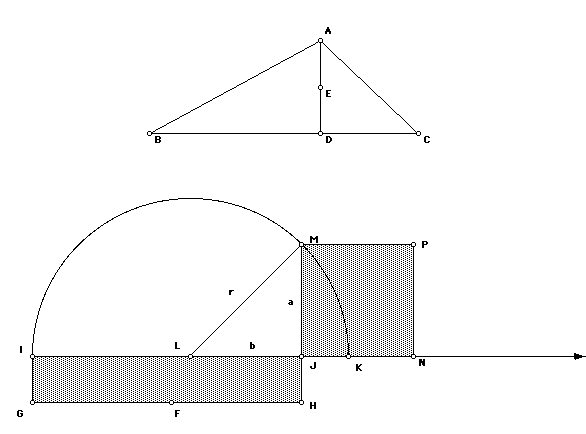
$Graphic2$

First Step: Construct a rectangle with an area equal to the triangle assumed to be ABC. For this bisect the height AD at E. Now the rectangle HJIG with width IJ = BC and height JH = ED has the same area as the triangle ABC.

Now extend IJ marking a point K with KJ=JH. Draw a circle using L as midpoint of IK and radius LI = LK. Extend JH and take intersection point M on circle. Use JM as side and construct square JMPN. This has the same area as HJIG and thus the same area as the triangle ABC.

a² = r²-b² = (r-b)(r+b). The length of HJIG is r+b and its height is r-b. Therefore the area of JMPN is equal to the area of HJIG and this itself is equal to the area of the triangle ABC.

Since any convex polygon can be squared then the next question is can be a circle be squared? The first who provided a step towards a possible solution was Hippocrates of Chios.

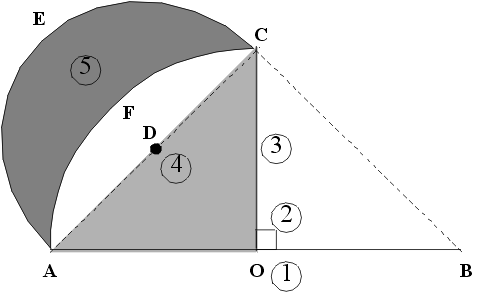
$Graphic3$

ABC is half a square inscribed in a semi-circle (A->B->C). Then a semi-circle is constructed on AC. CO is then constructed, the perpendicular bisector of AB, and triangle AOC is shaded, as is the part of the outer semi-circle that's not part of the original semicircle.

Hippocrates of Chios was able to show that the area of the “Lune” (a lune is a curved shape bounded by two circular arcs whose radii are different)AEC (The dark area number 5) is equal to the area of the triangle AOC (area 4).

Hippocrates of Chios ( (not Kos! )) spent his life studying geometry after becoming a victim of fraud in Byzantium and losing all his money. According to Proclus, he wrote about "Elements of Geometry" which was later lost like all other texts written during this century. In one of his works Simplicius (VIth century A.D.) states that he had copied extracts from Eudemus' "History of Mathematics" which is also now lost. In his work Simplicius describes part of the work of Hippocrates about the quadrature of lunes along with the following theorem: "Similar segments of circles are in the same ratio as the squares on their bases"

The lune is produced by taking the circle with radius AO forming the triangle AOC and the semi circle with the diameter AC and radius AD = AC/2.

We can say that the area of the quarter-circle bounded by CO and OA is 1/4*(pi*AO^2), or (pi*AO²)/4. The semicircle with edge AC, has an area of 1/2*(pi*(1/2 AC)²), or 1/2*(pi*1/4*AC²). But since AC = AO*sqrt(2), this is the same as 1/2*(pi*2*1/4AO²), or (pi*AO²)/4. Subtracting the region between the Semicircle AC and the minor arc AC, we find that the areas of the two regions set out in the problem are the same.

So if it is possible to “square” the lune why should it not possible to square the entire circle? Finding the square of a figure means finding the side of a square so that its area is equal to the area of the figure. So the “quadrature” of the circle is the problem to find the side of a square so that the area of the square is equal to the area of the circle.

Some say that Hippocrates was actually not able to provide a proof since he had to know that the ratio of areas of two circles is proportional to the ratio of the square of their diameter. To show this requires advanced methods such as the exhaustion methods by Eudoxus and Archimedes.

A real number is said to be algebraic if it is a solution of some polynomial equation with integer coefficients, i.e. a solution of

a_nxⁿ + a_n-1 x^n-1+...+a₂x² + a₁x¹+ a₀ = 0

A real number is transcendental if it is not algebraic. Then it is also not constructible, i.e. it is impossible to create it using only a straightedge and a compass.

Many future mathematicians tried but ultimately failed until Ferdinand Lindemann (1852 - 1939) proved that it was logically impossible! In 1880 he showed that the number PI =3.14159...was transcendental thus not constructible by ruler and compass.

A comment about the solution of Hippocrates is given by Carlo Cellucci:

Reducing a problem to another one (anagoghè). The prototype of this form of reasoning is provided by the Hippocrates of Chios’ solution to the problem of the quadrature of certain lunes. For example, Hippocrates reduces the question of the quadrature of the lune with an outer circumference equal to a semi-circle to the problem of establishing “that similar segments of circles have the same ratio to one another as their bases in square”, then he reduces the latter to the problem of establishing that “the diameters have the same ratio in square as the circles”, and so on (Eudemus 1955, p. 60). Reduction “is a transition from a problem or a theorem to another which, if known or constructed, would make the original proposition evident” (Proclus 1992, p. 167). Hippocrates’ procedure does not start from given principles, so it does not presuppose a systematic ordering of propositions determining strict precedence relations. Unlike the principles of the system of Euclid’s Elements, the hypotheses to which the problem of the quadrature of the lune is successively reduced are not intended as principles for the whole of geometry, adequate to solve every geometrical problem, but only a specific problem. Hippocrates’ method is further developed by Plato who introduces a procedure from hypotheses “formally identical to the one used by Hippocrates of Chios in his solution to the problem of the quadrature of the lunes” (Cambiano 1967, p. 136). Carlo Cellucci, The Growth of Mathematical Knowledge: An Open World View

Eves, Howard An Introduction to the History of Mathematics.(3rd ed.) Holt, New York, 1969. p. 67.

Some report also, that Thales and Hippocrates the mathematician traded; and that Plato defrayed the charges of his travels by selling oil in Egypt. Solon By Plutarch

Links

Peculiar Circle Squaring: A survey of the main texts relating to two attempts to square a circle (find a square equal to a circle), as reported initially by Aristotle.

Antiphon, a sophist around 500 BC.
Bryson (mid-4th cent. BC.)

Hippocrates of Chios, The area problem

Ancient Greece

Science, Technology , Medicine , Warfare, , Biographies , Life , Cities/Places/Maps , Arts , Literature , Philosophy ,Olympics, Mythology , History , Images