The Creation of the Universe, the Big Bang , with Plato's Polyhedra as elementary building blocks, especially important the dodecahedron. Stamp 2004

Polyhedra are solid figures bounded by plane polygons. A polyhedron bounded by a number of congruent polygonal faces, so that the same number of faces meet at each vertex, and in each face all the sides and angles are equal (i.e. faces are regular polygons) is called a regular polyhedron. Although Polyhedra are discussed in Euclid and the name is derived from “poly (many)” and “hedra (base)”, this name was used probably only more than 1500 years later in translations of Euclid's Elements. Euclid did not provide a completely correct definition of the regular polyhedra.

One morning the young Werner Heisenberg discovered reading Plato's Timaeus a description of the world with regular polyhedra. Heisenberg could not understand why Plato being so rational started to use speculative ideas. But finally he was fascinated by the idea that it could be possible to describe the Universe mathematically. He could not understand why Plato used the Polyhedra as the basic units in his model, but Heisenberg considered that in order to understand the world it is necessary to understand the Physics of the atoms.

Niels Bohr, and Werner Heisenberg on the right side with his wife in Greece (Acropolis , Parthenon 1955), Heisenberg's father was a professor of medieval and modern Greek studies at the University of Munich in Germany. Heisenberg had more a “humanistic” education, i.e. more Latin and Greek than in natural sciences.

... the five so-called Platonic figures which, however, do not belong to Plato, three of the five being due to the Pythagoreans, namely the cube, the pyramid, and the dodecahedron, while the octahedron and the icosahedron are due to Theaetetus. Geminus

Theaetetus (c. 414-367 BC), was a member of Plato's Academy. He was a son of Euphronius of Sounion, student of Theodore of Cyrene. Theaetetus died on his return to Athens after he was wounded at the Battle of Corinth. His friend Plato dedicated one of his dialogues to him. Euclid's elements chapter X and XIII are based on the work of Theaetetus.

Hippasus, from Metapontum in Magna Graecia (south Italy), who wrote around 465 BC about a "sphere of 12 pentagons" refers to the dodecahedron. Hippasus performed acoustics Experiments with vessels filled with different amounts of water and with cooper discs of different thicknesses.

Besides tutoring Eudoxos, some historians assume that Archytas also tutored Plato in mathematics point during the ten years that Plato spent in Sicily and Southern Italy. Plato was impressed by Archytas showing him that only five regular solid forms exist; the tetrahedron, cube, octahedron, dodecahedron and the icosahedron. Plato develop a whole mathematical theory using these geometrical objects to associate these with the four elements the fire, earth, water and air. And because one polyhedron was left he introduced the “ether” or “quintessence”. In using triangles as building blocks for the geometric objects he developed something like our “quarks” as building blocks of the “Platonic solids”. He was impressed by the mathematical beauty like today superstring theorists are impressed by the mathematical beauty of their theory independent of the existence of any experimental verification. In this way he was the first “theoretical elementary particle physicist...“

“To earth, then, let us assign the cubic form, for earth is the most immovable of the four and the most plastic of all bodies, and that which has the most stable bases must of necessity be of such a nature. Now, of the triangles which we assumed at first, that which has two equal sides is by nature more firmly based than that which has unequal sides, and of the compound figures which are formed out of either, the plane equilateral quadrangle has necessarily a more stable basis than the equilateral triangle, both in the whole and in the parts. Wherefore, in assigning this figure to earth, we adhere to probability, and to water we assign that one of the remaining forms which is the least movable, and the most movable of them to fire, and to air that which is intermediate. Also we assign the smallest body to fire, and the greatest to water, and the intermediate in size to air, and, again, the acutest body to fire, and the next in acuteness to air, and the third to water. Of all these elements, that which has the fewest bases must necessarily be the most movable, for it must be the acutest and most penetrating in every way, and also the lightest as being composed of the smallest number of similar particles, and the second body has similar properties in a second degree, and the third body, in the third degree. Let it be agreed, then, both according to strict reason and according to probability, that the pyramid is the solid which is the original element and seed of fire, and let us assign the element which was next in the order of generation to air, and the third to water. We must imagine all these to be so small that no single particle of any of the four kinds is seen by us on account of their smallness, but when many of them are collected together, their aggregates are seen. And the ratios of their numbers, motions, and other properties, everywhere God, as far as necessity allowed or gave consent, has exactly perfected and harmonized in due proportion.“
Plato: Timaeus (55d-56c) p 1181

Plato held the view that mathematical objects "really" existed so that they are discovered by mathematicians (in the same way that new continents are discovered by explorers) rather than invented. Plato believed that mathematics provided the best training for thinking about science and philosophy. The five regular solids are named "Platonic Solids" today after Plato.

Of the 5 solids, the tetrahedron has the smallest volume for its surface area and the icosahedron the largest; they therefore show the properties of dryness and wetness respectively and so correspond to FIRE and WATER. The cube, standing firmly on its base, corresponds to the stable EARTH but the octahedron which rotates freely when held by two opposite vertices, corresponds to the mobile AIR. The dodecahedron corresponds to the UNIVERSE because the zodiac has 12 signs (the constellations of stars that the sun passes through in the course of one year) corresponding to the 12 faces of the dodecahedron.

The 5 regular Platonic Polyhedra: Convex solids with identical regular polygon faces and identical vertices

Download PDF Files with paper models of the Archimedian and Platonic solids

Plato explains the four elements and their transformations:

In the first place, we see that what we just now called water, by condensation, I suppose, becomes stone and earth, and this same element, when melted and dispersed, passes into vapor and air. Air, again, when inflamed, becomes fire, and, again, fire, when condensed and extinguished, passes once more into the form of air, and once more, air, when collected and condensed, produces cloud and mist--and from these, when still more compressed, comes flowing water, and from water comes earth and stones once more--and thus generation appears to be transmitted from one to the other in a circle. Thus, then, as the several elements never present themselves in the same form, how can anyone have the assurance to assert positively that any of them, whatever it may be, is one thing rather than another? No one can. But much the safest plan is to speak of them as follows. Anything which we see to be continually changing, as, for example, fire, we must not call 'this' or 'that,' but rather say that it is 'of such a nature,' nor let us speak of water as 'this,' but always as 'such,' nor must we imply that there is any stability in any of those things which we indicate by the use of the words 'this' and 'that,' supposing ourselves to signify something thereby, for they are too volatile to be detained in any such expressions as 'this,' or 'that,' or 'relative to this,' or any other mode of speaking which represents them as permanent. We ought not to apply 'this' to any of them, but rather the word 'such,' which expresses the similar principle circulating in each and all of them; for example, that should be called 'fire' which is of such a nature always, and so of everything that has generation. That in which the elements severally grow up, and appear, and decay, is alone to be called by the name 'this' or 'that,' but that which is of a certain nature, hot or white, or anything which admits of opposite qualities, and all things that are compounded of them, ought not to be so denominated. Let me make another attempt to explain my meaning more clearly. Suppose a person to make all kinds of figures of gold and to be always remodeling each form into all the rest; somebody points to one of them and asks what it is. By far the safest and truest answer is, 'That is gold,' and not to call the triangle or any other figures which are formed in the gold 'these,' as though they had existence, since they are in process of change while he is making the assertion, but if the questioner be willing to take the safe and indefinite expression, 'such,' we should be satisfied. And the same argument applies to the universal nature which receives all bodies--that must be always called the same, for, inasmuch as she always receives all things, she never departs at all from her own nature and never, in any way or at any time, assumes a form like that of any of the things which enter into her; she is the natural recipient of all impressions, and is stirred and informed by them, and appears different from time to time by reason of them. But the forms which enter into and go out of her are the likenesses of eternal realities modeled after their patterns in a wonderful and mysterious manner, which we will hereafter investigate. For the present we have only to conceive of three natures: first, that which is in process of generation; secondly, that in which the generation takes place; and thirdly, that of which the thing generated is a resemblance naturally produced. And we may liken the receiving principle to a mother, and the source or spring to a father, and the intermediate nature to a child, and may remark further that if the model is to take every variety of form, then the matter in which the model is fashioned will not be duly prepared unless it is formless and free from the impress of any of those shapes which it is hereafter to receive from without. For if the matter were like any of the supervening forms, then whenever any opposite or entirely different nature was stamped upon its surface, it would take the impression badly, because it would intrude its own shape. Wherefore that which is to receive all forms should have no form, as in making perfumes they first contrive that the liquid substance which is to receive the scent shall be as inodorous as possible, or as those who wish to impress figures on soft substances do not allow any previous impression to remain, but begin by making the surface as even and smooth as possible. In the same way that which is to receive perpetually and through its whole extent the resemblances of all eternal beings ought to be devoid of any particular form. Wherefore the mother and receptacle of all created and visible and in any way sensible things is not to be termed earth or air or fire or water, or any of their compounds, or any of the elements from which these are derived, but is an invisible and formless being which receives all things and in some mysterious way partakes of the intelligible, and is most incomprehensible. In saying this we shall not be far wrong; as far, however, as we can attain to a knowledge of her from the previous considerations, we may truly say that fire is that part of her nature which from time to time is inflamed, and water that which is moistened, and that the mother substance becomes earth and air, in so far as she receives the impressions of them. Plato: Timaeus (49b-51c) p 1176

The Dual of a Solid

There are two important relationships between the dodecahedron and the icosahedron. First, the mid-points of the faces of the dodecahedron define the points on an icosahedron and the mid-points of the faces of an icosahedron define a dodecahedron. The same is true of the cube and the octahedron. If we try it with a tetrahedron, we just get another tetrahedron. Each is called the dual of the other solid where the number of edges in each pair is the same, but the number of faces of one is the number of points of the other, and vice-versa. Plato probably did not know this. Plato describes the basic elements of the “polyhedral atoms”:

Now is the time to explain what was before obscurely said. There was an error in imagining that all the four elements might be generated by and into one another; this, I say, was an erroneous supposition, for there are generated from the triangles which we have selected four kinds--three from the one which has the sides unequal, the fourth alone framed out of the isosceles triangle. Hence they cannot all be resolved into one another, a great number of small bodies being combined into a few large ones, or the converse. But three of them can be thus resolved and compounded, for they all spring from one, and when the greater bodies are broken up, many small bodies will spring up out of them and take their own proper figures. Or, again, when many small bodies are dissolved into their triangles, by their total number, they can form one large mass of another kind. So much for their passage into one another. I have now to speak of their several kinds, and show out of what combinations of numbers each of them was formed. The first will be the simplest and smallest construction, and its element is that triangle which has its hypotenuse twice the lesser side. When two such triangles are joined at the diagonal, and this is repeated three times, and the triangles rest their diagonals and shorter sides on the same point as a center, a single equilateral triangle is formed out of six triangles, and four equilateral triangles, if put together, make out of every three plane angles one solid angle, being that which is nearest to the most obtuse of plane angles. And out of the combination of these four angles arises the first solid form which distributes into equal and similar parts the whole circle in which it is inscribed. The second species of solid is formed out of the same triangles, which unite as eight equilateral triangles and form one solid angle out of four plane angles, and out of six such angles the second body is completed. And the third body is made up of one hundred and twenty triangular elements, forming twelve solid angles, each of them included in five plane equilateral triangles, having altogether twenty bases, each of which is an equilateral triangle. The one element [that is, the triangle which has its hypotenuse twice the lesser side], having generated these figures, generated no more, but the isosceles triangle produced the fourth elementary figure, which is compounded of four such triangles, joining their right angles in a center, and forming one equilateral quadrangle. Six of these united form eight solid angles, each of which is made by the combination of three plane right angles; the figure of the body thus composed is a cube, having six plane quadrangular equilateral bases. There was yet a fifth combination which God used in the delineation of the universe with figures of animals. Plato: Timaeus (54b-55c) p 1180

The last statement sounds strange and the meaning is not so clear. Plato also says “The Earth, if to look at it from above, is similar to the ball consisting of 12skin's pieces"

I have found different explanations by others:

The French geologist de Bimon and Poincare considered that the form of the Earth represents by itself the deformed dodecahedron. The Russian geologist Kislitsin also used in his researches the idea about the dodecahedral form of the Earth according to which 400-500 millions years ago the geo-sphere of the dodecahedral form was turn into the geo-icosahedron. As the result the geo-dodecahedron appeared to be inscribed into the frame of the icosahedron.

Others consider these animals to represent the zodiac cycle (since zoo means animal in Greek).

Another explanation maybe is that the pentagon is associated with the golden section and the corresponding ratio is observed in various biological systems.

.

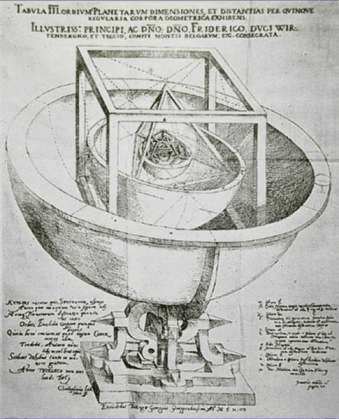
Wherefore it is clear that the very ratios of the planetary intervals from the sun have not been taken from the regular solids alone. For the Creator, who is the very source of geometry and, as Plato wrote, ‘practices eternal geometry,’ does not stray from his own archetype.” Thus, God, the eternal geometer must have given us the Platonic solids on behalf of the planetary orbit structure. They were made for each other. Johannes Kepler, “Harmonies of the World”, translated by Charles Glenn Wallis, Great Books of the Western World, Vol. 16, (Encyclopaedia Britannica, 1952), pp. 1017-18. The Science of the Harmony of the World (1619)

Kepler was also influenced by Plato's Ideas and he used Plato's regular solids to describe planetary motion as shown in a Figure above. He assigned the cube to Saturn, the tetrahedron to Jupiter, the dodecahedron to Mars, the icosahedron to Venus, and the octahedron to Mercury.

Luca Pacioli (1445-1517), inventor of the double bookkeeping method, in a stamp shown with a dodecahedron. (Italian Stamp, 1994 Michel 2319)

Pacioli devotes the second part of his book De Divina Proportione, published around 1509, to the Platonic solids. He writes:

As God brought into being the celestial virtue, the fifth essence, and through it created the four solids . . . earth, air, water, and fire ... so our sacred proportion gave shape to heaven itself, in assigning to it the dodecahedron . . . the solid of twelve pentagons, which cannot be constructed without our sacred proportion. As the aged Plato described in his Timaeus.

It is interesting to note that nature likes some of these geometrical shapes for example in crystals. We find basic crystal units in the form of a cube, octahedron in NaCL and CaF₂ respectively.

Back to Heisenberg:

...But the resemblance of the modern views to those of Plato and the Pythagoreans can be carried somewhat further. The elementary particles in Plato's Timaeus are finally not substance but mathematical forms. "All things are numbers" is a sentence attributed to Pythagoras. The only mathematical forms available at that time were such geometric forms as the regular solids or the triangles which form their surface. In modern quantum theory there can be no doubt that the elementary particles will finally also be mathematical forms but of a much more complicated nature. The Greek philosophers thought of static forms and found them in the regular solids. Modern science, however, has from its beginning in the sixteenth and seventeenth centuries started from the dynamic problem. The constant element in physics since Newton is not a configuration or a geometrical form, but a dynamic law. The equation of motion holds at all times, it is in this sense eternal, whereas the geometrical forms, like the orbits, are changing. Therefore, the mathematical forms that represent the elementary particles will be solutions of some eternal law of motion for matter. This is a problem which has not yet been solved. Heisenberg, Physics and Philosophy: The Revolution in Modern Science

Finally there is also a interesting comment by Nicholas Gier and Gail Adele:

... the most amazing vindication of Plato has come from recent surveys of the universe that indicate that the universe may indeed be a dodecahedron, whose reflecting pentagonal faces give the illusion of an infinite universe when in fact it is finite. See New Scientist (October, 2003). See www.newscientist.com/news

TIME

What is time and did time exist before the Universe was created? Plato's answer is that: time is an image of eternity:

When the father and creator saw the creature which he had made moving and living, the created image of the eternal gods, he rejoiced, and in his joy determined to make the copy still more like the original, and as this was an eternal living being, he sought to make the universe eternal, so far as might be. Now the nature of the ideal being was everlasting, but to bestow this attribute in its fullness upon a creature was impossible. Wherefore he resolved to have a moving image of eternity, and when he set in order the heaven, he made this image eternal but moving according to number, while eternity itself rests in unity, and this image we call time. For there were no days and nights and months and years before the heaven was created, but when he constructed the heaven he created them also. They are all parts of time, and the past and future are created species of time, which we unconsciously but wrongly transfer to eternal being, for we say that it 'was,' or 'is,' or 'will be,' but the truth is that 'is' alone is properly attributed to it, and that 'was' and 'will be' are only to be spoken of becoming in time, for they are motions, but that which is immovably the same forever cannot become older or younger by time, nor can it be said that it came into being in the past, or has come into being now, or will come into being in the future, nor is it subject at all to any of those states which affect moving and sensible things and of which generation is the cause. These are the forms of time, which imitates eternity and revolves according to a law of number. Moreover, when we say that what has become is become and what becomes is becoming, and that what will become is about to become and that the nonexistent is nonexistent – all these are inaccurate modes of expression. But perhaps this whole subject will be more suitably discussed on some other occasion. Plato, Timaeus 37c-38b

Comments by others

Ha Le:

... Plato tells how Timaeus of Locri thought of the Universe as being enveloped by a gigantic dodecahedron while the other four solids represent the "elements" of fire, air, earth, and water. Euclid's monumental treatise, the Elements , begins with the equilateral triangle, and culminates in the five Platonic solids, which are again the subject of the extra books XIV and XV (added a few centuries later). Sir D'Arcy W. Thompson once remarked that Euclid never dreamed of writing an Elementary Geometry. What Euclid really did was to write a very excellent account of the regular solids, for the use of Initiates.

Robinson Fredenthal, Sculpture, University Library Gallery, Baltimore, 1981. http://www.design.upenn.edu/rf/aboutrf.html

I can’t think of anything more perfect than a tetrahedron. If someone came here from outer space, I’d hand them a tetrahedron, and they would understand. I’m sure people discover these things over and over again in different cultures. They are essential parts of the universe; they are parts of order, and, as such, they represent our order. Art of the Tetrahedron

Selected fragments from THE PYTHAGOREAN SOURCE BOOK AND LIBRARY:

ii.6; Dox.334 Pythagoras: The universe is made from five solid figures which are also called mathematical; of these he says that earth has risen from the cube, fire from the pyramid, air from the octahedron, and water from the icosahedron,and the sphere of the All from the dodecahedron.

We should of course not forget that I presented only selections from Timaeus. I found a introduction of a translation of Timaeus interesting:

LINKS

A finite, dodecahedral universe

Plato's cosmology

The Most Beautiful Triangle - Timaeus Plato's

Theaetetus

How Many Regular Polyhedrons Are There In This or Any Universe?

POLYHEDRA & PLAGIARISMin the RENAISSANCE

Platonic Polyhedra from Euclid's Elements

Polyhedra Gallery

Convex Polyhedra

Platonic Solids: General Mathematical Formulas and Their Derivations

Platonic Solids in all dimensions

Platonions

Plato's Molecule , Prinzbach, H., et al. Gas-phase production and photoelectron spectroscopy of the smallest fullerene, C20. Nature 407, (7 Sept)60, 2000.

Is the Universe a Dodecahedron (in Greek)

Carl Gauss's Fundamental Theorem of Algebra

Interesting Links

Werner Heisenberg 1901 - 1976

Audio samples from http://www.paricenter.com/library/audio/index.php

Werner Heisenberg on the development of quantum theory http://www.paricenter.com/library/download/aaheis03.mp3 900 kb

Werner Heisenberg on language in quantum theory http://www.paricenter.com/library/download/heis03.mp3 800 kb

Michele Emmer. Art and mathematics: the Platonic solids. The Visual Mind, 215-220, Leonardo Book Series, MIT Press, Cambridge, Mass., 1993

D. H. Fowler , The Mathematics of Plato's Academy

Polyhedra, Peter R. Cromwell, Cambridge University Press, 1997. 451 pp. ISBN 0-521-55432

Miscellaneous

Poly , a shareware program for exploring and constructing polyhedra

Das Pentagondodekaeder von Schwarzenacker (The dodecahedron of Schwarzenacker)

Ancient Greece Science, Technology , Medicine , Warfare, , Biographies , Life , Cities/Places/Maps , Arts , Literature , Philosophy ,Olympics, Mythology , History , Images Medieval Greece / Byzantine Empire Science, Technology, Arts, , Warfare , Literature, Biographies, Icons, History Modern Greece Cities, Islands, Regions, Fauna/Flora ,Biographies , History , Warfare, Science/Technology, Literature, Music , Arts , Film/Actors , Sport , Fashion --- Cyprus Greek-Library - Scientific Library