.

Die Messung des Erdumfangs nach Eratosthenes

Δεῖ οὖν ἀναγκαίως καὶ τὸ ἀπο Συήνης εἰς Ἀλεξάνδρειαν διάστημα πεντηκοστὸν εἶναι μέρος τοῦ μεγίστου τῆς γῆς κύκλου · καὶ ἐστι τοῦτο σταδίων πεντακισχιλίων. ὁ ἄρα σύμπας κύκλος γίνεται μυριάδων εἴκοσι πέντε. Cleomedes, On the Circular Motions of the Celestial Bodies (de motu circulari corporum coelestium) And it is necessary that the distance between Syene and Alexandria is one-fiftieth of the Earth's circumference. Since this distance is 5000 stades the circumference length is 250000 stades.

Eratosthenes of Cyrene (c. 276 BC Cyrene – c. 194 BC Alexandria ), a friend of Archimedes of Syracuse, lived in Alexandria. He was born in Cyrene, a place in Libya which is called today Shahhat. He worked on geometry and prime numbers. He was a director of the great Library of Alexandria. He is best remembered for his prime number sieve which, in modified form, is still an important tool in number theory research. Eratosthenes measured the tilt of the Earth's axis with great accuracy and compiled a star catalogue containing 675 stars (now lost); he suggested that a leap day be added every fourth year and tried to construct an accurately-dated history. He became blind in his old age and is said to have committed suicide by starvation, like Democrit. Eratosthenes came to Alexandria from Athens to be the chief librarian of Ptolemy Euergetes. He was not merely an astronomer and a geographer, but a poet and grammarian as well. His contemporaries jestingly called him Beta the Second, because he was said through the universality of his attainments to be "a second Plato" in philosophy, "a second Thales" in astronomy, and so on throughout the list. For the same reason he was called a Pentathlos which means and athlete in five disciplines. We know indirect what he did by Strabo and Cleomedes who wrote 150-200 years later about Eratosthenes.

BOOKS

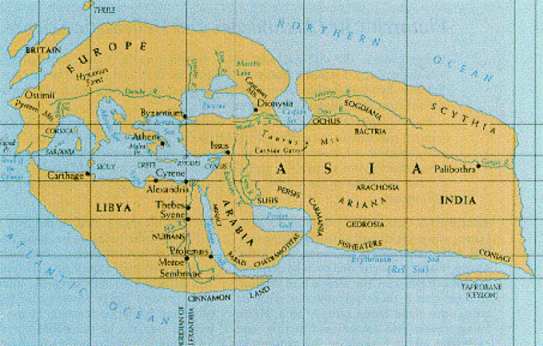
Geographica with maps and information of distance measurements. The map by Eratosthenes includes India, Sri-Lanka (Ceylon) and UK up to Thule in the North visited by Pytheas.

Stories and Poems such as Hermes and Epigone.

Thales made measurements with the aid of shadows using the gnomon, which is the most primitive, but which long remained the most important, of astronomical instruments. It is believed that Eratosthenes invented an important modification of the gnomon which was elaborated afterwards by Hipparchus and called an armillary sphere. This consists essentially of a small gnomon, or perpendicular post, attached to a plane representing the Earth's equator and a hemisphere in imitation of the Earth's surface. With the aid of this, the shadow cast by the sun could be very accurately measured. It involves no new principle. Every perpendicular post or object of any kind placed in the sunlight casts a shadow from which the angles now in question could be roughly measured. The armillary sphere made angle measurements extremely accurate.

Peri tês anametrêseôs tês gês (On the measurement of the earth)

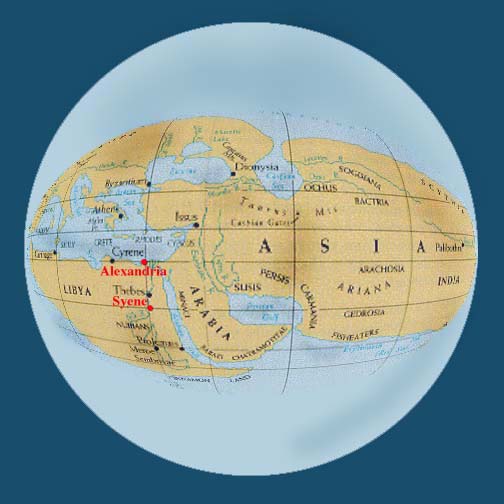
The ancient city of Syene (today known as أسوان ''Aswān'' or Assouan) is located due south of Alexandria at a distance of 5000 Greek stades.

In Syene there is a very deep well. Every year at noon on the day of the summer solstice (21 June) the sunlight illuminates the water at the bottom of this well. At that moment, the sun is directly overhead and there are no shadows in the city of Syene.

Eratosthenes invented, probably around 205 BC, a very beautiful method to measure the circumference of the Earth. Details of his method he published in a work On the measurement of the Earth which unfortunately was lost. We know indirect about his method from other authors, mainly Cleomedes and Theon of Smyrna. He noted that, on the summer solstice, the sun casts no shadow in Syene but he knew that it casts a shadow in Alexandria, north of Syene, corresponding to an angle α = 7^o 12' (or approximate 7.2^o). He obtained the angle α from the length of a shadow cast at noon by the summer solstice sun in Alexandria by a perpendicular object of known height, such as an obelisk or a gnomon. He reasoned that the change in angle of the shadow was caused by the spherical shape of the Earth (Aristotle and others knew this earlier) and that it would be possible from this angle to obtain the circumference of the Earth..

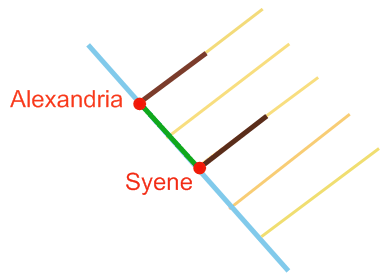
Grafik1

a) Assumption that the Earth is flat: If the sun light falls vertical in Syene then it will be also vertical in Alexandria and objects that are vertical in both cities, like an obelisk or a gnomon, will be parallel to the sun rays (no shadow will be observed). Eratosthenes knew that the sun is very far from the Earth so that the sun rays are almost perfectly parallel. Eratosthenes measured the distance to the sun as 804000000 stadia and the distance to the Moon as 780000 stadia from data obtained during lunar eclipses.

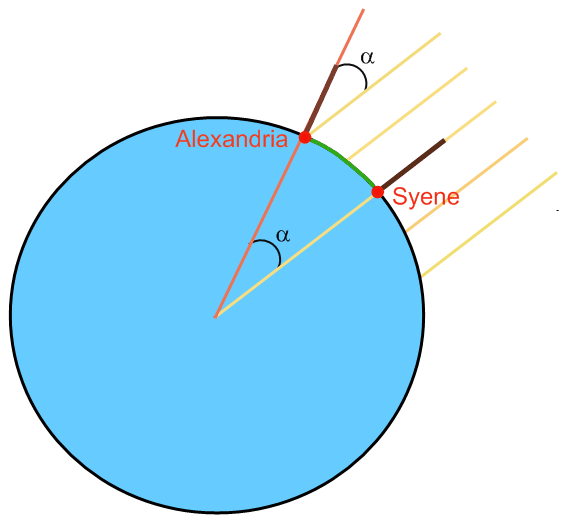
b) Assumption that the Earth is spherical: sun light which falls vertical in Syene forms an angle α with a vertical object in Alexandria due to the curvature of the Earth surface.

Καὶ ἐπὶ μὲν ταύτης βέβηκε περιφέρεια ἡ ἀπ’ ἄκρου τῆς σκιᾶς τοῦ γνώμονος ἐπὶ τὴν βάσιν αὐτοῦ περιαχθεῖσα, ἐπὶ δὲ τῆς πρὸς τῷ κέντρῳ τῆς γῆς ἡ ἀπο Συήνης διὴκουσα εἰς Ἀλεξάνδρειαν. Ὅμοιαι τοίνυν αἱ περιφέρειαί εἰσιν ἀλλήλαις ἐπ’ ἴσων γε γωνιῶν βεβηκυῖαι. Ὃν ἄρα λόγον ἔχει ἡ ἐν τῇ σκάφῃ πρὸς τὸν οἰκεῖον κύκλον, τοῦτον ἔχει τὸν λόγον καὶ ἡ ἀπὸ ἀπο Συήνης εἰς Ἀλεξάνδρειαν ἤκουσα. Cleomedes

If we extend the lines of two vertical objects they will meet at the center of the Earth and the angle formed by these two lines will be also equal to the angle α. Eratosthenes determined that the two cities were α = 7.2 degrees apart. That is to say, out of the 360 degrees needed to travel all the way around the world, the two cities were 7.2/360 (1/50) of that distance. In other words he determined that the distance between Alexandria and Syene was one-fiftieth of the Earth's circumference. Since he knew that the two cities were about 800 km apart, he concluded that the the Earth must be 50 * 800 km in circumference, or 40000 km (or roughly 25000 miles). From this he determined the circumference of the Earth to within less than 2% accuracy!!
2200 years ago!!!

Some Remarks

The distance between Alexandria and Syene is 729 km, not 800 km;
The accuracy depends on the length of the stadium. For a value of 157.2 metres for 1 stadium Eratosthenes obtained a remarkable accurate result but others suggest that the stadium was 166.7 metres.

- The two cities are not on the same meridian;

- Syene is not on the Tropic of Cancer (it is situated 55 km farther North);

The angular difference is not 7^o 12' but 7^o 5'.

Very interesting is that the measurement of the distance between Alexandria and Syene is based on the estimated average speed of a caravan of camels that traveled this distance(!). Camels traveled the distance many times to obtain an average estimate of the distance. Whether this is true is not clear.

About the well in Syene actually around 4% of the light is reflected from water and even this is enough to assume that it was dangerous to see the reflected sunlight from the water at noon local solar time at the summer solistice ( according to Edward Collett the reflected light is estimated to be 10000 more bright than that of the full moon). Therefore one can imagine that at that particular time one could not see at the reflected sunlight from the well (was there any water in the well?)

Strabo the known Geographer, another source of the experiment, says that Eratosthenes obtained 252000 and not 250000 stades

Some even say that Eratosthenes used another method , the so called dip-method: Obviously, academic-socialite Eratosthenes simply used or adopted the dip-method result (which could have involved merely ordmag an hour’s work atop the famous lighthouse, as against weeks of wearing & dangerous travel from Alexandria to Aswan) — not the method for which he has been unjustly immortalized. DIO & The Journal for Hysterical Astronomy (PDF File)

Finally there is also the posibility that he used a scaphe which is also a sun dial.

Grafik2

The scaphe dial, probably the oldest form of sundials. Scaphe (Greek boat) a bowl-shaped cup within which the hour-lines are marked. At the time of summer solstice the shadow is shortest and falls exactly on the bottom line. In the following time the shadow grows again until it reaches the top line at the time of winter solstice. The days are divided into temporal hours. Their length is not fixed but instead the time between sunrise and sunset is divided into 12 intervals of equal length. Klaus Kohl provides a possible method used by Eratosthenes with the scaphe to determine the circumference, avoiding the measurement of angles.

Two thousand years later, French astronomers Pierre Méchain and Jean-Baptiste Delambre set out to measure the Earth using modern methods. Their goal was to determine with precision and accuracy the distance between the Earth's north pole and its equator. By dividing that great distance into ten million equal parts, the savants, in the name of the people of France and the good of all mankind, would create a new and natural standard of measure: the meter.

According to Ptolemy Eratosthenes measured the tilt of the Earth's axis and obtained a value of ¹¹/₈₃ of 180 degrees.

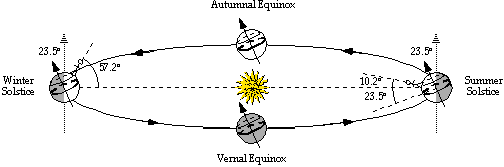
The Earth's orbit around the Sun is very nearly circular, and it defines a plane in space called the ecliptic plane. With respect to the perpendicular to the ecliptic plane (which points to orbital north), the Earth's axis is tilted at an angle of 23.5°:

When the Earth's north pole is tilted directly towards the Sun, the latter is highest in the sky (in the northern hemisphere), which is what we called the summer solstice.

When the north pole is tilted directly away from the Sun, the latter is lowest in the sky (in the northern hemisphere), which is the winter solstice. The intermediate positions are the vernal and autumnal equinoxes.

How did Eratosthenes discover the method to determine the Earth diameter? In the Science Fiction book Summer Solstice by Charles L. Harness (nominated for a Nebula award in 1985) Eratosthenes meets a shipwrecked alien, and if we ignore the many historical errors, learns from the alien how to do this! Today we do not know exactly which method he used, but he knew one or more methods to estimate the size of the Earth, all equal impressive.

Some Images and part of Information from Department of History
University of California, Irvine
Dr. Barbara J. Becker

For more details see the Metrum Website!

On Eratosthenes, Maui's Voyage of Discovery, and Reviving The Principle of Discovery Today by Lyndon H. LaRouche, Jr.

Klaus Kohl, Die Erdmessung des Eratosthenes (PDF File in German)

Measuring the Earth with Traceroute (PDF File) a modern version of estimating the Earth size using a computer and recording the roundtrip time for small Internet packets between major Internet traffic hubs (a method much less accurate than all variations of Eratosthenes! which also requires the existence of a network).

A 100 pages PDF File (in English) (in Spanish or French) with information about the Eratosthenes Experiment and what students and teachers need to know to do this experiment

Comments by Vitruvius

Those who know names for very many winds will perhaps be surprised at our setting forth that there are only eight. Remembering, however, that Eratosthenes of Cyrene, employing mathematical theories and geometrical methods, discovered from the course of the sun, the shadows cast by an equinoctial gnomon, and the inclination of the heaven that the circumference of the earth is two hundred and fifty-two thousand stadia, that is, thirty-one million five hundred thousand paces, and observing that an eighth part of this, occupied by a wind, is three million nine hundred and thirty-seven thousand five hundred paces, they should not be surprised to find that a single wind, ranging over so wide a field, is subject to shifts this way and that, leading to a variety of breezes.

Eratosthenes lunar crater

German

Klaus Geus, Eratosthenes von Kyrene. Studien zur hellenistischen Kultur- und Wissenschaftsgeschichte. Münchener Beiträge zur Papyrusforschung und antiken Rechtsgeschichte, 92. München: C. H. Beck, 2002. Pp. 413. ISBN 3-406-48976-1. (English Review)

LINKS

Eratosthenes Experiment: A Worldwide Science and Math Experiment

Ancient Greece

Science, Technology , Medicine , Warfare, , Biographies , Life , Cities/Places/Maps , Arts , Literature , Philosophy ,Olympics, Mythology , History , Images