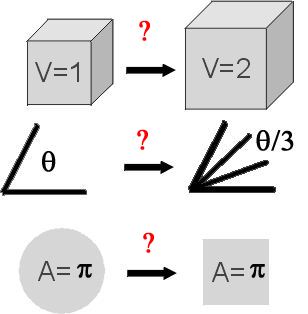
The classic cube doubling, angle trisection and squaring the circle problems.

Trying to solve the classical problems of Antiquity, such as the trisection problem, Greeks discovered different mathematical curves. There was no systematic theory of higher-degree curves in Greek mathematics but Greeks studied many interesting special cases:

• The Cissoid of Diocles ( c. 100 BC )

Diocles showed that the Cissoid a cubic curve defined by y² (1+x) = (1-x)³ could be used to duplicate the cube

• The Spiric Sections of Perseus ( c. 150 BC )

• The Epicycles of Ptolemy ( c. 140 AD ) used to describe the retrograde motion of Planets in his Earth centric model.

• Ellipse, Parabola, Hyperbola (Conic Sections) discovered probably by Menaechmus and theory studied in details by Apollonius.

Xah Lee has a very interesting Website that includes also information of Curves among which some have been discovered by ancient Greek mathematicians. I provide the links to the corresponding plane curves. Later I will provide additional information. Also other links are provided.

CURVE	LINKS
Archimedean Spiral	Archimedean Spiral
Conchoid of Nicomedes	Conchoid of Nicomedes Pappus on Nicomedes' cochloid (conchoid)
Cissoid of Diocles	Cissoid of Diocles Cissoid and burning mirrors
Spiric of Perseus	Spiric of Perseus
General Conic Sections	Conic Sections
Ellipse	Ellipse
Hyperbola	Hyperbola
Parabola	Parabola
Quadratix of Hippias	A Crowning Achievement: The Quadratrix of Hippias Quadratrix of Hippias Pappus on the Quadratrix Construction from a cylindrical spiral, as the intersection of a plektoid and a plane Construction from an Archimedes spiral, as the intersection of a plektoid and a plane
Hippopede of Proclus (and Eudoxus)	The Hippopede of Proclus (and Eudoxus) The Hippopede of Proclus
Philon's Line	The Philon's Line

Derivation of the Formula for the Area of a Circle and the Pythagorean Theorem

LINKS

Vignettes of Ancient Mathematics by Henry Mendell, Cal. State U., L.A.

Ancient Greece Science, Technology , Medicine , Warfare, , Biographies , Life , Cities/Places/Maps , Arts , Literature , Philosophy ,Olympics, Mythology , History , Images Medieval Greece / Byzantine Empire Science, Technology, Arts, , Warfare , Literature, Biographies, Icons, History Modern Greece Cities, Islands, Regions, Fauna/Flora ,Biographies , History , Warfare, Science/Technology, Literature, Music , Arts , Film/Actors , Sport , Fashion --- Cyprus Greek-Library - Scientific Library