.

Kegelschnitte: Apollonius und Menaechmus

HYPATIA: Today's subject is conic sections, slices of a cone. A cone — you should be able to remember this — a dunce cap? By passing planes through the cone, various geometric shapes are generated at the intersections. Cut on the horizontal, perpendicular to the axis, we have a circle. Cut at a slight angle, we have an ellipse. Increase the angle a bit more, a parabola.
(Draws on the board) Let us consider the parabola. Where do we find it in nature?
(No response) Come, now. Parse the word. Para — for, bola — throwing. For throwing. What shape is described when you throw a ball into the air? Certainly, a parabola. What shape is described when a furious mob hurls paving stones at the heads of innocent people? Parabolas, all of them... Gerald Everett Jones Hypatia of Alexandria

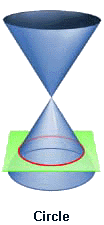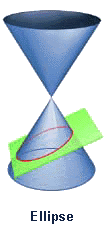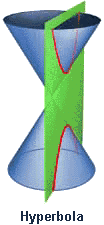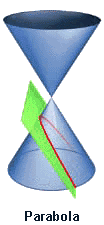
$Graphic4$
A conic section (red curve) is the result of an intersection between a cone and a plane. Depending on the angle of intersection, the result can be a hyperbola, parabola, circle, or ellipse.

It is Apollonius of Perga (Απολλώνιος ο Περγαίος ) (about 262 BC - about 190 BC), a Greek geometer, who is usually considered the inventor of the conic sections that leads to the circle, ellipse, parabola and hyperbola that are the possible trajectories of a body in a gravitational field (At least if we ignore some relativistic effects). Apollonius is known as the "Great Geometer" based on his work Conics (Conic secions) , an eight-"book" series on the subject. As he writes ..... I undertook the investigation of this subject at the request of Naucrates the geometer, at the time when he came to Alexandria and stayed with me.. The first four books have come down to us in the original Ancient Greek, but books V-VII are known only from an Arabic translation, while the eighth book has been lost entirely. The Conics is one of the most difficult and complex known mathematical work of ancient Greek mathematicians. Hilal ibn Hilal al-Himsi translated the first four volumes of the Conics while book V to VII were translated by Thabit ibn Qurrah. The Conics is one of the most important mathematical books ever written!

Apollonius wrote many books but only the Conics survived partly. Other books considered that he has written area

1) Cutting-off of an Area
2) Cutting-off of a Ratio
3) Inclinations
4) Plane Loci
5) Quick Delivery (With and unknown method that provides an approximation of 3.1416 for pi )
6) Tangencies

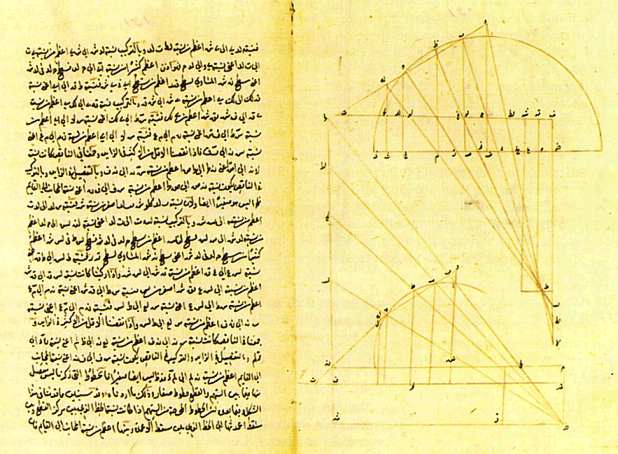
Arabic translation of the Apollonius book V on Conic Sections.

Apollonius used the so-called Symptoms that describes a constant relation between varying magnitudes that depend on the position of an arbitrary point on a curve, example a point C on a parabola. If |AE|= |ED| then AC is a tangent to the parabola

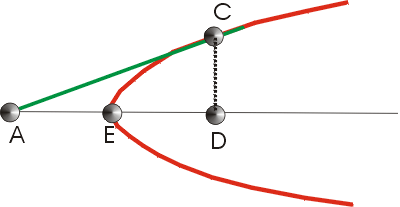
Apollonius showed that only a single normal line can be assigned to each point of a conic section (Coolidge). In the fifth book he discusses evolutes and centers of curvature (Cajori) (or osculation as mentioned by Euler in Introductio in analysin infinitorum 1748 ). Apollonius therefore was of the first who considered the curvature and elements of differential geometry.

Menaechmus (Μέναιχμος ) (from Alopeconnesus or Proconnesus) earlier (about 380 BC- about 320 BC) showed that circle, ellipses, parabolas, and hyperbolas are obtained by cutting a cone with a plane. He was born in Alopeconnesus, (now Turkey) and was a student of Plato and Eudoxus. Aristaeus and Euclid also studied conic sections like Archimedes but no publications from him is known directly.
An Arabic translation of the work of Diocles On burning mirrors discovered in the 1970s, led G J Toomer to claim that both the names 'parabola' and 'hyperbola' are older than Apollonius.

An ancient tragic poet had represented Minos as dissatisfied with a tomb which he had put up to Glaucus, and which was only 100 feet each way. He therefore ordered it to be made double the size, the poet making him add that each dimension should be doubled for this purpose(!). The poet was, as showed von Wilamowitz, not Aeschylus or Sophocles or Euripides, but some obscure person who owes the notoriety of his lines to his ignorance of mathematics.

This problem, and the accompanying story, is presented in a letter from Eratosthenes of Cyrene to King Ptolemy Euergetes, which has come down to us as quoted by Eutocius in his commentary on Archimedes' On the Sphere and Cylinder. Eratosthenes told Ptolemy that the legendary King Minos wished to build a tomb for Glaucus and felt that its current dimensions - one hundred feet on each side - were inadequate.

Too small thy plan to bound a royal tomb.
Let it be double; yet of its fair form
Fail not, but haste to double every side.
(Heath, 1961, p. xvii)

Another reason of this Problem is that the Delians were told by the oracle of Apollo at Delos that, if they would get rid of a certain plague (430 BC), they should construct an altar of double the size of the existing one. They consulted therefore Plato who replied that the oracle meant, not that god wanted an altar of double the size, but that he intended, in setting them the task, to shame the Greeks for their neglect of mathematics and their contempt for geometry.

The conic sections have been considered by others before who tried to solve the problem of duplicating the cube. The specific problem considered by Menaechmus was to find two mean proportionals between two straight lines. He solved in this way the problem of the duplicating the cube using conic sections. Menaechmus's solution is described by Eutocius in his commentary to Archimedes “On the sphere and cylinder”.

A breakthrough occurred when Hippocrates of Chios reduced the problem to the equivalent problem of "two mean proportionals", though this formulation turned out to be no easier to handle than the previous one (Heath, 1961, p. xviii). Suppose that we are given a, b and we want to find two mean proportionals x, y between them. Then a : x = x : y = y : b then then a/x = x/y so x² = ay, and a/x = y/b so xy = ab.

The values of x and y are found from the intersection of the parabola x² = ay and the rectangular hyperbola xy = ab. Once we have this, we can take the special case a=2b to double the cube.

But had Menaechmus really have a construction involving a cone in mind when he solved the problem of doubling the cube? Heath argues that he did, for the following reason. In the same letter from Eratosthenes to Ptolemy mentioned above, Eratosthenes stated, in connection with a discussion of his own solution to the problem, that there is no need to resort to "cutting the cone in the triads of Menaechmus" (Heath, 1961, xviii). In addition to this quotation appearing in Eutocius' commentary on Archimedes, Proclus confirms that conics were discovered by Menaechemus (Heath, 1961, xix) ...

How did he think of obtaining these curves from a cone ? Though there is virtually no information on this question itself, intuition tells us that the keen observational skills of Greek mathematicians would be attracted to such shapes. It is likely that the first conic section noticed in nature would have been an ellipse. If one cuts a cylinder at an angle other than a right angle to its axis, the result is an ellipse. In fact, Euclid notes in his Phenomena that a cone or cylinder cut by a plane not parallel to the base results in a section of an acute-angled cone which is "similar to a [shield]" (Heath, 1921, 125). A natural extension of this phenomena would by the cutting of a cone in a similar fashion. Then perhaps they moved the cutting plane so that it does not cut the cone completely. What types of curves result? How are each of their properties similar to the other sections? How are they different? This is a possible, and probably simplified, discussion of the flowing of ideas that led to the study of conic sections.

Some consider that in reality astronomical observations were the reason of the studies of elliptical curves and conical sections in general. Probably they were discovered from the work of Greeks with sundials, considering for example the problem of the intersection of a light cone with a plane.

Application of Conic Sections

The work of Menaechmus and Apollonius was quite theoretical although we have seen that there was a specific problem to be solved. Nevertheless the most significant application had to wait eighteen centuries until Johannes Kepler used the ellipse for the orbits of planets (or others objects) or orbits of satellites.

I have found the following information of the possible use of conics section in Greek Architecture:

In this view of the Parthenon, one can observe the "upward curvature" of the stylobate (the platform on which the columns rest). In fact, there are no straight lines anywhere in the Parthenon. Everything is slightly curved. In particular, the deep foundation, the stylobate, and the entablature is higher in the center (ca. 2 1/2 inches on the short sides and ca. 4 1/2 inches on the flanks) than it is an the corners. This upward curvature is found in some other Doric temples, but the Parthenon is the most exaggerated and perfect example. The curve appears to be parabolic (a regular conic section). http://www.willamette.edu/cla/wviews/slides.cgi?p4 . According to Caratheodory the Mathematician this cannot be true probably as this would suggest that the conic sections were known during by Iktinos and Kallikrates. Caratheodory considers the case that circles have been used with a very large radius instead for the Parthenon.

Three dimensional versions of the planar two dimensional conic sections have been used by the Greeks in mathematical studies. Diocles the mathematician in his work On burning mirrors was the first to prove the focal property of a parabolic mirror. Applications of the parabolic reflector today: satellite dishes, optic and radio telescopes, parabolic microphones, lighting devices

This is often cited as an example of the value of pure mathematics: Let the mathematicians do what interests them and applications will appear later.

Other Mathematicians

Conon of Samos, a mathematician and astronomer, author of Pros Thrasydaion (a letter with conics related problem, sent to Thrasydaeus) which was lost, but mentioned by Apollonius of Perga.

Eudemus of Pergamum and his student Philonides the geometer, Naucrates the geometer. Naucrates visited Apollonius in Alexandria, Eudemus and Apollonius had a meeting in Ephesus. Apollonius son, also called Apollonius, visited Eudemus with copies of the books of his father. The Conics were dedicated to Attalus I Soter, the ruler of Pergamum (241-197), who probably supported Apollonius.

References

Greek Geometry from Thales to Euclid

Cajori, Florian. A History of Mathematics. New York: MacMillan and Co., 1894.
Coolidge,J.L. "The Unsatisfactory Story of Curvature." The American Mathematical Monthly. vol. 59, number 6. New York: McGraw-Hill Book Co., Inc, 1952.
Heath, T.L. A History of Greek Mathematics, volume I, II. (1921). Oxford University: New York.

Links

Hyperbolic Functions: A Fugue Across 25 Centuries by Bruce Director
Earliest Known Uses of Some of the Words of Mathematics
The Conic Sections and Dandelin Spheres (A word doc file .. Rename to Dandelin Spheres.doc to view)
A Note: Why Modern Mathematicians Can't Understand Archytas
Archytas’s Musical Construction (and the Conics) by Fletcher James