.
The Legacy of GREECE
Essays by Gilbert Murray, W. R. Inge, J. Burnet, Sir T. L. Heath, D’Arcy W. Thompson, Charles Singer, R. W. Livingston, A. Toynbee, A. E. Zimmern, Percy Gardner, Sir Reginald Blomfield
Edited by
R. W. LIVINGSTONE

OXFORD
AT THE CLARENDON PRESS
PRINTED IN ENGLAND AT THE
UNIVERSITY PRESS, OXFORD
BY JOHN JOHNSON
PRINTER TO THE UNIVERSITY
Transcriber’s Note
Short fragments of Greek text have a thin dotted blue underline. The transliterated version appears in a transient pop-up box when the mouse hovers over the words.
Longer Greek phrases and poems are followed by the transliterated version in braces.
[97]
MATHEMATICS AND ASTRONOMY
It has been well said that, if we would study any subject properly, we must study it as something that is alive and growing and consider it with reference to its growth in the past. As most of the vital forces and movements in modern civilization had their origin in Greece, this means that, to study them properly, we must get back to Greece. So it is with the literature of modern countries, or their philosophy, or their art; we cannot study them with the determination to get to the bottom and understand them without the way pointing eventually back to Greece.
When we think of the debt which mankind owes to the Greeks, we are apt to think too exclusively of the masterpieces in literature and art which they have left us. But the Greek genius was many-sided; the Greek, with his insatiable love of knowledge, his determination to see things as they are and to see them whole, his burning desire to be able to give a rational explanation of everything in heaven and earth, was just as irresistibly driven to natural science, mathematics, and exact reasoning in general, or logic.
To quote from a brilliant review of a well-known work: ‘To be a Greek was to seek to know, to know the primordial substance of matter, to know the meaning of number, to know the world as a rational whole. In no spirit of paradox one may say that Euclid is the most typical Greek: he would know to the bottom, and know as a rational system, the laws of the measurement of the earth. Plato, too, loved geometry and the wonders of numbers; he was essentially Greek because he was essentially mathematical.... And if one thus finds the [98] Greek genius in Euclid and the Posterior Analytics, one will understand the motto written over the Academy, μηδεις αγεωμετρητος εισιτω. To know what the Greek genius meant you must (if one may speak εν αινιγματι) begin with geometry.’
Mathematics, indeed, plays an important part in Greek philosophy: there are, for example, many passages in Plato and Aristotle for the interpretation of which some knowledge of the technique of Greek mathematics is the first essential. Hence it should be part of the equipment of every classical student that he should have read substantial portions of the works of the Greek mathematicians in the original, say, some of the early books of Euclid in full and the definitions (at least) of the other books, as well as selections from other writers. Von Wilamowitz-Moellendorff has included in his Griechisches Lesebuch extracts from Euclid, Archimedes and Heron of Alexandria; and the example should be followed in this country.
Acquaintance with the original works of the Greek mathematicians is no less necessary for any mathematician worthy of the name. Mathematics is a Greek science. So far as pure geometry is concerned, the mathematician’s technical equipment is almost wholly Greek. The Greeks laid down the principles, fixed the terminology and invented the methods ab initio; moreover, they did this with such certainty that in the centuries which have since elapsed there has been no need to reconstruct, still less to reject as unsound, any essential part of their doctrine.
Consider first the terminology of mathematics. Almost all the standard terms are Greek or Latin translations from the Greek, and, although the mathematician may be taught their meaning without knowing Greek, he will certainly grasp their significance better if he knows them as they arise and as part of the living language of the men who invented them. Take the word isosceles; a schoolboy can be shown what an isosceles [99] triangle is, but, if he knows nothing of the derivation, he will wonder why such an apparently outlandish term should be necessary to express so simple an idea. But if the mere appearance of the word shows him that it means a thing with equal legs, being compounded of ισος, equal, and σκελος, a leg, he will understand its appropriateness and will have no difficulty in remembering it. Equilateral, on the other hand, is borrowed from the Latin, but it is merely the Latin translation of the Greek ισοπλευρος, equal-sided. Parallelogram again can be explained to a Greekless person, but it will be far better understood by one who sees in it the two words παραλληλος and γραμμη and realizes that it is a short way of expressing that the figure in question is contained by parallel lines; and we shall best understand the word parallel itself if we see in it the statement of the fact that the two straight lines so described go alongside one another, παρ’ αλληλας, all the way. Similarly a mathematician should know that a rhombus is so called from its resemblance to a form of spinning-top (ῥομβος from ῥεμβω, to spin) and that, just as a parallelogram is a figure formed by two pairs of parallel straight lines, so a parallelepiped is a solid figure bounded by three pairs of parallel planes (παραλληλος, parallel, and επιπεδος, plane); incidentally, in the latter case, he will be saved from writing ‘parallelopiped’, a monstrosity which has disfigured not a few textbooks of geometry. Another good example is the word hypotenuse; it comes from the verb ὑποτεινειν (c. ὑπο and acc. or simple acc.), to stretch under, or, in its Latin form, to subtend, which term is used quite generally for ‘to be opposite to’; in our phraseology the word hypotenuse is restricted to that side of a right-angled triangle which is opposite to the right angle, being short for the expression used in Eucl. i. 47, ἡ την ορθην γωνιαν ὑποτεινουσα πλευρα, ‘the side subtending the right angle’, which accounts for the feminine participial form ὑποτεινουσα, hypotenuse. If mathematicians had had[100] more Greek, perhaps the misspelt form ‘hypothenuse’ would not have survived so long.
To take an example outside the Elements, how can a mathematician properly understand the term latus rectum used in conic sections unless he has seen it in Apollonius as the erect side (ορθια πλευρα) of a certain rectangle in the case of each of the three conics?[3] The word ordinate can hardly convey anything to one who does not know that it is what Apollonius describes as ‘the straight line drawn down (from a point on the curve) in the prescribed or ordained manner (τεταγμενως κατηγμενη)’. Asymptote again comes from ασυμπτωτος, non-meeting, non-secant, and had with the Greeks a more general signification as well as the narrower one which it has for us: it was sometimes used of parallel lines, which also ‘do not meet’.
Again, if we take up a textbook of geometry written in accordance with the most modern Education Board circular or University syllabus, we shall find that the phraseology used (except where made more colloquial and less scientific) is almost all pure Greek. The Greek tongue was extraordinarily well adapted as a vehicle of scientific thought. One of the characteristics of Euclid’s language which his commentator Proclus is most fond of emphasizing is its marvellous exactness (ακριβεια). The language of the Greek geometers is also wonderfully concise, notwithstanding all appearances to the contrary. One of the complaints often made against Euclid is that he is ‘diffuse’. Yet (apart from abbreviations in writing) it will be found that the exposition of corresponding [101] matters in modern elementary textbooks generally takes up, not less, but more space. And, to say nothing of the perfect finish of Archimedes’s treatises, we shall find in Heron, Ptolemy and Pappus veritable models of concise statement. The purely geometrical proof by Heron of the formula for the area of a triangle, Δ=√{s(s-a) (s-b) (s-c)}, and the geometrical propositions in Book I of Ptolemy’s Syntaxis (including ‘Ptolemy’s Theorem’) are cases in point.
The principles of geometry and arithmetic (in the sense of the theory of numbers) are stated in the preliminary matter of Books I and VII of Euclid. But Euclid was not their discoverer; they were gradually evolved from the time of Pythagoras onwards. Aristotle is clear about the nature of the principles and their classification. Every demonstrative science, he says, has to do with three things, the subject-matter, the things proved, and the things from which the proof starts (εξ ὡν). It is not everything that can be proved, otherwise the chain of proof would be endless; you must begin somewhere, and you must start with things admitted but indemonstrable. These are, first, principles common to all sciences which are called axioms or common opinions, as that ‘of two contradictories one must be true’, or ‘if equals be subtracted from equals, the remainders are equal’; secondly, principles peculiar to the subject-matter of the particular science, say geometry. First among the latter principles are definitions; there must be agreement as to what we mean by certain terms. But a definition asserts nothing about the existence or non-existence of the thing defined. The existence of the various things defined has to be proved except in the case of a few primary things in each science the existence of which is indemonstrable and must be assumed among the first principles of the science; thus in geometry we must assume the existence of points and lines, and in arithmetic of the unit. Lastly, we must assume certain other things which are [102] less obvious and cannot be proved but yet have to be accepted; these are called postulates, because they make a demand on the faith of the learner. Euclid’s Postulates are of this kind, especially that known as the parallel-postulate.
The methods of solution of problems were no doubt first applied in particular cases and then gradually systematized; the technical terms for them were probably invented later, after the methods themselves had become established.
One method of solution was the reduction of one problem to another. This was called απαγωγη, a term which seems to occur first in Aristotle. But instances of such reduction occurred long before. Hippocrates of Chios reduced the problem of duplicating the cube to that of finding two mean proportionals in continued proportion between two straight lines, that is, he showed that, if the latter problem could be solved, the former was thereby solved also; and it is probable that there were still earlier cases in the Pythagorean geometry.
Next there is the method of mathematical analysis. This method is said to have been ‘communicated’ or ‘explained’ by Plato to Leodamas of Thasos; but, like reduction (to which it is closely akin), analysis in the mathematical sense must have been in use much earlier. Analysis and its correlative synthesis are defined by Pappus: ‘in analysis we assume that which is sought as if it were already done, and we inquire what it is from which this results, and again what is the antecedent cause of the latter, and so on, until by so retracing our steps we come upon something already known or belonging to the class of principles. But in synthesis, reversing the process, we take as already done that which was last arrived at in the analysis, and, by arranging in their natural order as consequences what were before antecedents and successively connecting them one with another, we arrive finally at the construction of that which was sought.’
The method of reductio ad absurdum is a variety of analysis. [103] Starting from a hypothesis, namely the contradictory of what we desire to prove, we use the same process of analysis, carrying it back until we arrive at something admittedly false or absurd. Aristotle describes this method in various ways as reductio ad absurdum, proof per impossibile, or proof leading to the impossible. But here again, though the term was new, the method was not. The paradoxes of Zeno are classical instances.
Lastly, the Greeks established the form of exposition which still governs geometrical work, simply because it is dictated by strict logic. It is seen in Euclid’s propositions, with their separate formal divisions, to which specific names were afterwards assigned, (1) the enunciation (προτασις), (2) the setting-out (εκθεσις), (3) the διορισμος, being a re-statement of what we are required to do or prove, not in general terms (as in the enunciation), but with reference to the particular data contained in the setting-out, (4) the construction (κατασκευη), (5) the proof (αποδειξις), (6) the conclusion (συμπερασμα). In the case of a problem it often happens that a solution is not possible unless the particular data are such as to satisfy certain conditions; in this case there is yet another constituent part in the proposition, namely the statement of the conditions or limits of possibility, which was called by the same name διορισμος, definition or delimitation, as that applied to the third constituent part of a theorem.
We have so far endeavoured to indicate generally the finality and the abiding value of the work done by the creators of mathematical science. It remains to summarize, as briefly as possible, the history of Greek mathematics according to periods and subjects.
The Greeks of course took what they could in the shape of elementary facts in geometry and astronomy from the Egyptians and Babylonians. But some of the essential characteristics of the Greek genius assert themselves even in[104] their borrowings from these or other sources. Here, as everywhere else, we see their directness and concentration; they always knew what they wanted, and they had an unerring instinct for taking only what was worth having and rejecting the rest. This is illustrated by the story of Pythagoras’s travels. He consorted with priests and prophets and was initiated into the religious rites practised in different places, not out of religious enthusiasm ‘as you might think’ (says our informant), but in order that he might not overlook any fragment of knowledge worth acquiring that might lie hidden in the mysteries of divine worship.
This story also illustrates an important advantage which the Greeks had over the Egyptians and Babylonians. In those countries science, such as it was, was the monopoly of the priests; and, where this is the case, the first steps in science are apt to prove the last also, because the scientific results attained tend to become involved in religious prescriptions and routine observances, and so to end in a collection of lifeless formulae. Fortunately for the Greeks, they had no organized priesthood; untrammelled by prescription, traditional dogmas or superstition, they could give their reasoning faculties free play. Thus they were able to create science as a living thing susceptible of development without limit.
Greek geometry, as also Greek astronomy, begins with Thales (about 624-547 B. C.), who travelled in Egypt and is said to have brought geometry from thence. Such geometry as there was in Egypt arose out of practical needs. Revenue was raised by the taxation of landed property, and its assessment depended on the accurate fixing of the boundaries of the various holdings. When these were removed by the periodical flooding due to the rising of the Nile, it was necessary to replace them, or to determine the taxable area independently of them, by an art of land-surveying. We conclude from the Papyrus Rhind (say 1700 B. C.) and other documents that Egyptian geometry[105] consisted mainly of practical rules for measuring, with more or less accuracy, (1) such areas as squares, triangles, trapezia, and circles, (2) the solid content of measures of corn, &c., of different shapes. The Egyptians also constructed pyramids of a certain slope by means of arithmetical calculations based on a certain ratio, se-qeṭ, namely the ratio of half the side of the base to the height, which is in fact equivalent to the co-tangent of the angle of slope. The use of this ratio implies the notion of similarity of figures, especially triangles. The Egyptians knew, too, that a triangle with its sides in the ratio of the numbers 3, 4, 5 is right-angled, and used the fact as a means of drawing right angles. But there is no sign that they knew the general property of a right-angled triangle (= Eucl. I. 47), of which this is a particular case, or that they proved any general theorem in geometry.
No doubt Thales, when he was in Egypt, would see diagrams drawn to illustrate the rules for the measurement of circles and other plane figures, and these diagrams would suggest to him certain similarities and congruences which would set him thinking whether there were not some elementary general principles underlying the construction and relations of different figures and parts of figures. This would be in accord with the Greek instinct for generalization and their wish to be able to account for everything on rational principles.
The following theorems are attributed to Thales: (1) that a circle is bisected by any diameter (Eucl. I, Def. 17), (2) that the angles at the base of an isosceles triangle are equal (Eucl. I. 5), (3) that, if two straight lines cut one another, the vertically opposite angles are equal (Eucl. I. 15), (4) that, if two triangles have two angles and one side respectively equal, the triangles are equal in all respects (Eucl. I. 26). He is said (5) to have been the first to inscribe a right-angled triangle in a circle, which must mean that he was the first to discover that the angle in a semicircle is a right angle (cf. Eucl. III. 31).
[106] Elementary as these things are, they represent a new departure of a momentous kind, being the first steps towards a theory of geometry. On this point we cannot do better than quote some remarks from Kant’s preface to the second edition of his Kritik der reinen Vernunft.
‘Mathematics has, from the earliest times to which the history of human reason goes back, (that is to say) with that wonderful people the Greeks, travelled the safe road of a science. But it must not be supposed that it was as easy for mathematics as it was for logic, where reason is concerned with itself alone, to find, or rather to build for itself, that royal road. I believe on the contrary that with mathematics it remained for long a case of groping about—the Egyptians in particular were still at that stage—and that this transformation must be ascribed to a revolution brought about by the happy inspiration of one man in trying an experiment, from which point onward the road that must be taken could no longer be missed, and the safe way of a science was struck and traced out for all time and to distances illimitable.... A light broke on the first man who demonstrated the property of the isosceles triangle (whether his name was Thales or what you will)....’
Thales also solved two problems of a practical kind: (1) he showed how to measure the distance of a ship at sea, and (2) he found the heights of pyramids by means of the shadows thrown on the ground by the pyramid and by a stick of known length at the same moment; one account says that he chose the time when the lengths of the stick and of its shadow were equal, but in either case he argued by similarity of triangles.
In astronomy Thales predicted a solar eclipse which was probably that of the 28th May 585 B. C. Now the Babylonians, as the result of observations continued through centuries, had discovered the period of 223 lunations after which eclipses[107] recur. It is most likely therefore that Thales had heard of this period, and that his prediction was based upon it. He is further said to have used the Little Bear for finding the pole, to have discovered the inequality of the four astronomical seasons, and to have written works On the Equinox and On the Solstice.
After Thales come the Pythagoreans. Of the Pythagoreans Aristotle says that they applied themselves to the study of mathematics and were the first to advance that science, going so far as to find in the principles of mathematics the principles of all existing things. Of Pythagoras himself we are told that he attached supreme importance to the study of arithmetic, advancing it and taking it out of the region of practical utility, and again that he transformed the study of geometry into a liberal education, examining the principles of the science from the beginning.
The very word μαθηματα, which originally meant ‘subjects of instruction’ generally, is said to have been first appropriated to mathematics by the Pythagoreans.
In saying that arithmetic began with Pythagoras we have to distinguish between the uses of that word then and now. Αριθμητικη with the Greeks was distinguished from λογιστικη, the science of calculation. It is the latter word which would cover arithmetic in our sense, or practical calculation; the term αριθμητικη was restricted to the science of numbers considered in themselves, or, as we should say, the Theory of Numbers. Another way of putting the distinction was to say that αριθμητικη dealt with absolute numbers or numbers in the abstract, and λογιστικη with numbered things or concrete numbers; thus λογιστικη included simple problems about numbers of apples, bowls, or objects generally, such as are found in the Greek Anthology and sometimes involve simple algebraical equations.
The Theory of Numbers then began with Pythagoras (about [108] 572-497 B. C.). It included definitions of the unit and of number, and the classification and definitions of the various classes of numbers, odd, even, prime, composite, and sub-divisions of these such as odd-even, even-times-even, &c. Again there were figured numbers, namely, triangular numbers, squares, oblong numbers, polygonal numbers (pentagons, hexagons, &c.) corresponding respectively to plane figures, and pyramidal numbers, cubes, parallelepipeds, &c., corresponding to solid figures in geometry. The treatment was mostly geometrical, the numbers being represented by dots filling up geometrical figures of the various kinds. The laws of formation of the various figured numbers were established. In this investigation the gnomon played an important part. Originally meaning the upright needle of a sun-dial, the term was next used for a figure like a carpenter’s square, and then was applied to a figure of that shape put round two sides of a square and making up a larger square. The arithmetical application of the term was similar. If we represent a unit by one dot and put round it three dots in such a way that the four form the corners of a square, three is the first gnomon. Five dots put at equal distances round two sides of the square containing four dots make up the next square (3²), and five is the second gnomon. Generally, if we have n² dots so arranged as to fill up a square with n for its side, the gnomon to be put round it to make up the next square, (n+1)², has 2n+1 dots. In the formation of squares, therefore, the successive gnomons are the series of odd numbers following 1 (the first square), namely 3, 5, 7, ... In the formation of oblong numbers (numbers of the form n(n+1)), the first of which is 1. 2, the successive gnomons are the terms after 2 in the series of even numbers 2, 4, 6.... Triangular numbers are formed by adding to 1 (the first triangle) the terms after 1 in the series of natural numbers 1, 2, 3 ...; these are therefore the gnomons (by analogy) for triangles. The gnomons for pentagonal numbers[109] are the terms after 1 in the arithmetical progression 1, 4, 7, 10 ... (with 3, or 5-2, as the common difference) and so on; the common difference of the successive gnomons for an a-gonal number is a-2.
From the series of gnomons for squares we easily deduce a formula for finding square numbers which are the sum of two squares. For, the gnomon 2n+1 being the difference between the successive squares n² and (n+1)², we have only to make 2n+1 a square. Suppose that 2n+1=m²; therefore n=½(m²-1), and {½(m²-1)}²+m²={½(m²+1)}², where m is any odd number. This is the formula actually attributed to Pythagoras.
Pythagoras is said to have discovered the theory of proportionals or proportion. This was a numerical theory and therefore was applicable to commensurable magnitudes only; it was no doubt somewhat on the lines of Euclid, Book VII. Connected with the theory of proportion was that of means, and Pythagoras was acquainted with three of these, the arithmetic, geometric, and sub-contrary (afterwards called harmonic). In particular Pythagoras is said to have introduced from Babylon into Greece the ‘most perfect’ proportion, namely:
a:(a+b)/2=2ab/(a+b):b,
where the second and third terms are respectively the arithmetic and harmonic mean between a and b. A particular case is 12:9=8:6.
This bears upon what was probably Pythagoras’s greatest discovery, namely that the musical intervals correspond to certain arithmetical ratios between lengths of string at the same tension, the octave corresponding to the ratio 2:1, the fifth to 3:2 and the fourth to 4:3. These ratios being the same as those of 12 to 6, 8, 9 respectively, we can understand[110] how the third term, 8, in the above proportion came to be called the ‘harmonic’ mean between 12 and 6.
The Pythagorean arithmetic as a whole, with the developments made after the time of Pythagoras himself, is mainly known to us through Nicomachus’s Introductio arithmetica, Iamblichus’s commentary on the same, and Theon of Smyrna’s work Expositio rerum mathematicarum ad legendum Platonem utilium. The things in these books most deserving of notice are the following.
First, there is the description of a ‘perfect’ number (a number which is equal to the sum of all its parts, i.e. all its integral divisors including 1 but excluding the number itself), with a statement of the property that all such numbers end in 6 or 8. Four such numbers, namely 6, 28, 496, 8128, were known to Nicomachus. The law of formation for such numbers is first found in Eucl. IX. 36 proving that, if the sum (Sn) of n terms of the series 1, 2, 2², 2³ ... is prime, then Sn.2n-1 is a perfect number.
Secondly, Theon of Smyrna gives the law of formation of the series of ‘side-’ and ‘diameter-’ numbers which satisfy the equations 2x²-y²=±1. The law depends on the proposition proved in Eucl. II. 10 to the effect that (2x+y)²-2(x+y)²=2x²-y², whence it follows that, if x, y satisfy either of the above equations, then 2x+y, x+y is a solution in higher numbers of the other equation. The successive solutions give values for y/x, namely 1/1, 3/2, 7/5, 17/12, 41/29, ..., which are successive approximations to the value of √2 (the ratio of the diagonal of a square to its side). The occasion for this method of approximation to √2 (which can be carried as far as we please) was the discovery by the Pythagoreans of the incommensurable or irrational in this particular case.
Thirdly, Iamblichus mentions a discovery by Thymaridas, a Pythagorean not later than Plato’s time, called the επανθημα (‘bloom’) of Thymaridas, and amounting to the solution[111] of any number of simultaneous equations of the following form:
x+x1 + x2 + ... + xn-1 = s,
x + x1 = a1,
x + x2 = a2,
....
x+xn-1 = an-1,
the solution being x=((a1+a2+...+an-1)-s)/(n-2).
The rule is stated in general terms, but the above representation of its effect shows that it is a piece of pure algebra.
The Pythagorean contributions to geometry were even more remarkable. The most famous proposition attributed to Pythagoras himself is of course the theorem of Eucl. I. 47 that the square on the hypotenuse of any right-angled triangle is equal to the sum of the squares on the other two sides. But Proclus also attributes to him, besides the theory of proportionals, the construction of the ‘cosmic figures’, the five regular solids.
One of the said solids, the dodecahedron, has twelve regular pentagons for faces, and the construction of a regular pentagon involves the cutting of a straight line ‘in extreme and mean ratio’ (Eucl. II. 11 and VI. 30), which is a particular case of the method known as the application of areas. This method was fully worked out by the Pythagoreans and proved one of the most powerful in all Greek geometry. The most elementary case appears in Eucl. I. 44, 45, where it is shown how to apply to a given straight line as base a parallelogram with one angle equal to a given angle and equal in area to any given rectilineal figure; this construction is the geometrical equivalent of arithmetical division. The general case is that in which the parallelogram, though applied to the straight line, overlaps it or falls short of it in such a way that the part[112] of the parallelogram which extends beyond or falls short of the parallelogram of the same angle and breadth on the given straight line itself (exactly) as base is similar to any given parallelogram (Eucl. VI. 28, 29). This is the geometrical equivalent of the solution of the most general form of quadratic equation ax±mx²=C, so far as it has real roots; the condition that the roots may be real was also worked out (=Eucl. VI. 27). It is in the form of ‘application of areas’ that Apollonius obtains the fundamental property of each of the conic sections, and, as we shall see, it is from the terminology of application of areas that Apollonius took the three names parabola, hyperbola, and ellipse which he was the first to give to the three curves.
Another problem solved by the Pythagoreans was that of drawing a rectilineal figure which shall be equal in area to one given rectilineal figure and similar to another. Plutarch mentions a doubt whether it was this problem or the theorem of Eucl. I. 47 on the strength of which Pythagoras was said to have sacrificed an ox.
The main particular applications of the theorem of the square on the hypotenuse, e. g. those in Euclid, Book II, were also Pythagorean; the construction of a square equal to a given rectangle (Eucl. II. 14) is one of them, and corresponds to the solution of the pure quadratic equation x²=ab.
The Pythagoreans knew the properties of parallels and proved the theorem that the sum of the three angles of any triangle is equal to two right angles.
As we have seen, the Pythagorean theory of proportion, being numerical, was inadequate in that it did not apply to incommensurable magnitudes; but, with this qualification, we may say that the Pythagorean geometry covered the bulk of the subject-matter of Books I, II, IV and VI of Euclid’s Elements. The case is less clear with regard to Book III of the Elements; but, as the main propositions of that Book were known to Hippocrates of Chios in the second half of the fifth [113] century B. C., we conclude that they, too, were part of the Pythagorean geometry.
Lastly, the Pythagoreans discovered the existence of the incommensurable or irrational in the particular case of the diagonal of a square in relation to its side. Aristotle mentions an ancient proof of the incommensurability of the diagonal with the side by a reductio ad absurdum showing that, if the diagonal were commensurable with the side, it would follow that one and the same number is both odd and even. This proof was doubtless Pythagorean.
A word should be added about the Pythagorean astronomy. Pythagoras was the first to hold that the earth (and no doubt each of the other heavenly bodies also) is spherical in shape, and he was aware that the sun, moon and planets have independent movements of their own in a sense opposite to that of the daily rotation; but he seems to have kept the earth in the centre. His successors in the school (one Hicetas of Syracuse and Philolaus are alternatively credited with this innovation) actually abandoned the geocentric idea and made the earth, like the sun, the moon, and the other planets, revolve in a circle round the ‘central fire’, in which resided the governing principle ordering and directing the movement of the universe.
The geometry of which we have so far spoken belongs to the Elements. But, before the body of the Elements was complete, the Greeks had advanced beyond the Elements. By the second half of the fifth century B. C. they had investigated three famous problems in higher geometry, (1) the squaring of the circle, (2) the trisection of any angle, (3) the duplication of the cube. The great names belonging to this period are Hippias of Elis, Hippocrates of Chios, and Democritus.
Hippias of Elis invented a certain curve described by combining two uniform movements (one angular and the other rectilinear) taking the same time to complete. Hippias himself[114] used his curve for the trisection of any angle or the division of it in any ratio; but it was afterwards employed by Dinostratus, a brother of Eudoxus’s pupil Menaechmus, and by Nicomedes for squaring the circle, whence it got the name τετραγωνιζουσα, quadratrix.
Hippocrates of Chios is mentioned by Aristotle as an instance to prove that a man may be a distinguished geometer and, at the same time, a fool in the ordinary affairs of life. He occupies an important place both in elementary geometry and in relation to two of the higher problems above mentioned. He was, so far as is known, the first compiler of a book of Elements; and he was the first to prove the important theorem of Eucl. XII. 2 that circles are to one another as the squares on their diameters, from which he further deduced that similar segments of circles are to one another as the squares on their bases. These propositions were used by him in his tract on the squaring of lunes, which was intended to lead up to the squaring of the circle. The essential portions of the tract are preserved in a passage of Simplicius’s commentary on Aristotle’s Physics, which contains substantial extracts from Eudemus’s lost History of Geometry. Hippocrates showed how to square three particular lunes of different kinds and then, lastly, he squared the sum of a circle and a certain lune. Unfortunately the last-mentioned lune was not one of those which can be squared, so that the attempt to square the circle in this way failed after all.
Hippocrates also attacked the problem of doubling the cube. There are two versions of the origin of this famous problem. According to one story an old tragic poet had represented Minos as having been dissatisfied with the size of a cubical tomb erected for his son Glaucus and having told the architect to make it double the size while retaining the cubical form. The other story says that the Delians, suffering from a pestilence, consulted the oracle and were told to [115] double a certain altar as a means of staying the plague. Hippocrates did not indeed solve the problem of duplication, but reduced it to another, namely that of finding two mean proportionals in continued proportion between two given straight lines; and the problem was ever afterwards attacked in this form. If x, y be the two required mean proportionals between two straight lines a, b, then a:x=x:y=y:b, whence b/a=(x/a)³, and, as a particular case, if b=2a, x³=2a³, so that, when x is found, the cube is doubled.
Democritus wrote a large number of mathematical treatises, the titles only of which are preserved. We gather from one of these titles, ‘On irrational lines and solids’, that he wrote on irrationals. Democritus realized as fully as Zeno, and expressed with no less piquancy, the difficulty connected with the continuous and the infinitesimal. This appears from his dilemma about the circular base of a cone and a parallel section; the section which he means is a section ‘indefinitely near’ (as the phrase is) to the base, i. e. the very next section, as we might say (if there were one). Is it, said Democritus, equal or not equal to the base? If it is equal, so will the very next section to it be, and so on, so that the cone will really be, not a cone, but a cylinder. If it is unequal to the base and in fact less, the surface of the cone will be jagged, like steps, which is very absurd. We may be sure that Democritus’s work on ‘The contact of a circle or a sphere’ discussed a like difficulty.
Lastly, Archimedes tells us that Democritus was the first to state, though he could not give a rigorous proof, that the volume of a cone or a pyramid is one-third of that of the cylinder or prism respectively on the same base and having equal height, theorems first proved by Eudoxus.
We come now to the time of Plato, and here the great names are Archytas, Theodoras of Cyrene, Theaetetus, and Eudoxus.
[116] Archytas (about 430-360 B. C.) wrote on music and the numerical ratios corresponding to the intervals of the tetrachord. He is said to have been the first to write a treatise on mechanics based on mathematical principles; on the practical side he invented a mechanical dove which would fly. In geometry he gave the first solution of the problem of the two mean proportionals, using a wonderful construction in three dimensions which determined a certain point as the intersection of three surfaces, (1) a certain cone, (2) a half-cylinder, (3) an anchor-ring or tore with inner diameter nil.
Theodorus, Plato’s teacher in mathematics, extended the theory of the irrational by proving incommensurability in certain particular cases other than that of the diagonal of a square in relation to its side, which was already known. He proved that the side of a square containing 3 square feet, or 5 square feet, or any non-square number of square feet up to 17 is incommensurable with one foot, in other words that √3, √5 ... √17 are all incommensurable with 1. Theodorus’s proof was evidently not general; and it was reserved for Theaetetus to comprehend all these irrationals in one definition, and to prove the property generally as it is proved in Eucl. X. 9. Much of the content of the rest of Euclid’s Book X (dealing with compound irrationals), as also of Book XIII on the five regular solids, was due to Theaetetus, who is even said to have discovered two of those solids (the octahedron and icosahedron).
Plato (427-347 B. C.) was probably not an original mathematician, but he ‘caused mathematics in general and geometry in particular to make a great advance by reason of his enthusiasm for them’. He encouraged the members of his school to specialize in mathematics and astronomy; e. g. we are told that in astronomy he set it as a problem to all earnest students to find ‘what are the uniform and ordered movements by the assumption of which the apparent motions of the planets[117] may be accounted for’. In Plato’s own writings are found certain definitions, e. g. that of a straight line as ‘that of which the middle covers the ends’, and some interesting mathematical illustrations, especially that in the second geometrical passage in the Meno (86E-87C). To Plato himself are attributed (1) a formula (n²-1)²+(2n)²=(n²+1)² for finding two square numbers the sum of which is a square number, (2) the invention of the method of analysis, which he is said to have explained to Leodamas of Thasos (mathematical analysis was, however, certainly, in practice, employed long before). The solution, attributed to Plato, of the problem of the two mean proportionals by means of a frame resembling that which a shoemaker uses to measure a foot, can hardly be his.
Eudoxus (408-355 B. C.), an original genius second to none (unless it be Archimedes) in the history of our subject, made two discoveries of supreme importance for the further development of Greek geometry.
(1) As we have seen, the discovery of the incommensurable rendered inadequate the Pythagorean theory of proportion, which applied to commensurable magnitudes only. It would no doubt be possible, in most cases, to replace proofs depending on proportions by others; but this involved great inconvenience, and a slur was cast on geometry generally. The trouble was remedied once for all by Eudoxus’s discovery of the great theory of proportion, applicable to commensurable and incommensurable magnitudes alike, which is expounded in Euclid’s Book V. Well might Barrow say of this theory that ‘there is nothing in the whole body of the elements of a more subtile invention, nothing more solidly established’. The keystone of the structure is the definition of equal ratios (Eucl. V, Def. 5); and twenty-three centuries have not abated a jot from its value, as is plain from the facts that Weierstrass repeats it word for word as his definition of equal[118] numbers, and it corresponds almost to the point of coincidence with the modern treatment of irrationals due to Dedekind.
(2) Eudoxus discovered the method of exhaustion for measuring curvilinear areas and solids, to which, with the extensions given to it by Archimedes, Greek geometry owes its greatest triumphs. Antiphon the Sophist, in connexion with attempts to square the circle, had asserted that, if we inscribe successive regular polygons in a circle, continually doubling the number of sides, we shall sometime arrive at a polygon the sides of which will coincide with the circumference of the circle. Warned by the unanswerable arguments of Zeno against infinitesimals, mathematicians substituted for this the statement that, by continuing the construction, we can inscribe a polygon approaching equality with the circle as nearly as we please. The method of exhaustion used, for the purpose of proof by reductio ad absurdum, the lemma proved in Eucl. X. 1 (to the effect that, if from any magnitude we subtract not less than half, and then from the remainder not less than half, and so on continually, there will sometime be left a magnitude less than any assigned magnitude of the same kind, however small): and this again depends on an assumption which is practically contained in Eucl. V, Def. 4, but is generally known as the Axiom of Archimedes, stating that, if we have two unequal magnitudes, their difference (however small) can, if continually added to itself, be made to exceed any magnitude of the same kind (however great).
The method of exhaustion is seen in operation in Eucl. XII. 1-2, 3-7 Cor., 10, 16-18. Props. 3-7 Cor. and Prop. 10 prove that the volumes of a pyramid and a cone are one-third of the prism and cylinder respectively on the same base and of equal height; and Archimedes expressly says that these facts were first proved by Eudoxus.
In astronomy Eudoxus is famous for the beautiful theory of concentric spheres which he invented to explain the apparent [119] motions of the planets and, particularly, their apparent stationary points and retrogradations. The theory applied also to the sun and moon, for each of which Eudoxus employed three spheres. He represented the motion of each planet as produced by the rotations of four spheres concentric with the earth, one within the other, and connected in the following way. Each of the inner spheres revolves about a diameter the ends of which (poles) are fixed on the next sphere enclosing it. The outermost sphere represents the daily rotation, the second a motion along the zodiac circle; the poles of the third sphere are fixed on the latter circle; the poles of the fourth sphere (carrying the planet fixed on its equator) are so fixed on the third sphere, and the speeds and directions of rotation so arranged, that the planet describes on the second sphere a curve called the hippopede (horse-fetter), or a figure of eight, lying along and longitudinally bisected by the zodiac circle. The whole arrangement is a marvel of geometrical ingenuity.
Heraclides of Pontus (about 388-315 B. C.), a pupil of Plato, made a great step forward in astronomy by his declaration that the earth rotates on its own axis once in 24 hours, and by his discovery that Mercury and Venus revolve about the sun like satellites.
Menaechmus, a pupil of Eudoxus, was the discoverer of the conic sections, two of which, the parabola and the hyperbola, he used for solving the problem of the two mean proportionals. If a:x=x:y=y:b, then x²=ay, y²=bx and xy=ab. These equations represent, in Cartesian co-ordinates, and with rectangular axes, the conics by the intersection of which two and two Menaechmus solved the problem; in the case of the rectangular hyperbola it was the asymptote-property which he used.
We pass to Euclid’s times. A little older than Euclid, Autolycus of Pitane wrote two books, On the Moving Sphere, a work on Sphaeric for use in astronomy, and On Risings and [120] Settings. The former work is the earliest Greek textbook which has reached us intact. It was before Euclid when he wrote his Phaenomena, and there are many points of contact between the two books.
Euclid flourished about 300 B. C. or a little earlier. His great work, the Elements in thirteen Books, is too well known to need description. No work presumably, except the Bible, has had such a reign; and future generations will come back to it again and again as they tire of the variegated substitutes for it and the confusion resulting from their bewildering multiplicity. After what has been said above of the growth of the Elements, we can appreciate the remark of Proclus about Euclid, ‘who put together the Elements, collecting many of Eudoxus’s theorems, perfecting many of Theaetetus’s and also bringing to irrefragable demonstration the things which were only somewhat loosely proved by his predecessors’. Though a large portion of the subject-matter had been investigated by those predecessors, everything goes to show that the whole arrangement was Euclid’s own; it is certain that he made great changes in the order of propositions and in the proofs, and that his innovations began at the very beginning of Book I.
Euclid wrote other books on both elementary and higher geometry, and on the other mathematical subjects known in his day. The elementary geometrical works include the Data and On Divisions (of figures), the first of which survives in Greek and the second in Arabic only; also the Pseudaria, now lost, which was a sort of guide to fallacies in geometrical reasoning. The treatises on higher geometry are all lost; they include (1) the Conics in four Books, which covered almost the same ground as the first three Books of Apollonius’s Conics, although no doubt, for Euclid, the conics were still, as with his predecessors, sections of a right-angled, an obtuse-angled, and an acute-angled cone respectively made by a plane perpendiular [121] to a generator in each case; (2) the Porisms in three Books, the importance and difficulty of which can be inferred from Pappus’s account of it and the lemmas which he gives for use with it; (3) the Surface-Loci, to which again Pappus furnishes lemmas; one of these implies that Euclid assumed as known the focus-directrix property of the three conics, which is absent from Apollonius’s Conics.
In applied mathematics Euclid wrote (1) the Phaenomena, a work on spherical astronomy in which ὁ ὁριζων (without κυκλος or any qualifying words) appears for the first time in the sense of horizon; (2) the Optics, a kind of elementary treatise on perspective: these two treatises are extant in Greek; (3) a work on the Elements of Music. The Sectio Canonis, which has come down under the name of Euclid, can, however, hardly be his in its present form.
In the period between Euclid and Archimedes comes Aristarchus of Samos (about 310-230 B. C.), famous for having anticipated Copernicus. Accepting Heraclides’s view that the earth rotates about its own axis, Aristarchus went further and put forward the hypothesis that the sun itself is at rest, and that the earth, as well as Mercury, Venus, and the other planets, revolve in circles about the sun. We have this on the unquestionable authority of Archimedes, who was only some twenty-five years later, and who must have seen the book containing the hypothesis in question. We are told too that Cleanthes the Stoic thought that Aristarchus ought to be indicted on the charge of impiety for setting the Hearth of the Universe in motion.
One work of Aristarchus, On the sizes and distances of the Sun and Moon, which is extant in Greek, is highly interesting in itself, though it contains no word of the heliocentric hypothesis. Thoroughly classical in form and style, it lays down certain hypotheses and then deduces therefrom, by rigorous geometry, the sizes and distances of the sun and [122] moon. If the hypotheses had been exact, the results would have been correct too; but Aristarchus in fact assumed a certain angle to be 87° which is really 89° 50', and the angle subtended at the centre of the earth by the diameter of either the sun or the moon to be 2°, whereas we know from Archimedes that Aristarchus himself discovered that the latter angle is only ½°. The effect of Aristarchus’s geometry is to find arithmetical limits to the values of what are really trigonometrical ratios of certain small angles, namely
1/18 > sin 3° > 1/20, 1/45 > sin 1° > 1/60, 1 > cos 1° > 89/90.
The main results obtained are (1) that the diameter of the sun is between 18 and 20 times the diameter of the moon, (2) that the diameter of the moon is between 2/45ths and 1/30th of the distance of the centre of the moon from our eye, and (3) that the diameter of the sun is between 19/3rds and 43/6ths of the diameter of the earth. The book contains a good deal of arithmetical calculation.
Archimedes was born about 287 B. C. and was killed at the sack of Syracuse by Marcellus’s army in 212 B. C. The stories about him are well known, how he said ‘Give me a place to stand on, and I will move the earth’ (πα βω και κινω ταν γαν; how, having thought of the solution of the problem of the crown when in the bath, he ran home naked shouting ἑυρηκα, ἑυρηκα; and how, the capture of Syracuse having found him intent on a figure drawn on the ground, he said to a Roman soldier who came up, ‘Stand away, fellow, from my diagram.’ Of his work few people know more than that he invented a tubular screw which is still used for pumping water, and that for a long time he foiled the attacks of the Romans on Syracuse by the mechanical devices and engines which he used against them. But he thought meanly of these things, and his real interest was in pure mathematical speculation; he caused to be engraved on his tomb a representation of a cylinder circumscribing [123] a sphere, with the ratio 3/2 which the cylinder bears to the sphere: from which we infer that he regarded this as his greatest discovery.
Archimedes’s works are all original, and are perfect models of mathematical exposition; their wide range will be seen from the list of those which survive: On the Sphere and Cylinder I, II, Measurement of a Circle, On Conoids and Spheroids, On Spirals, On Plane Equilibriums I, II, the Sandreckoner, Quadrature of the Parabola, On Floating Bodies I, II, and lastly the Method (only discovered in 1906). The difficult Cattle-Problem is also attributed to him, and a Liber Assumptorum which has reached us through the Arabic, but which cannot be his in its present form, although some of the propositions in it (notably that about the ‘Salinon’, salt-cellar, and others about circles inscribed in the αρβηλος, shoemaker’s knife) are quite likely to be of Archimedean origin. Among lost works were the Catoptrica, On Sphere-making, and investigations into polyhedra, including thirteen semi-regular solids, the discovery of which is attributed by Pappus to Archimedes.
Speaking generally, the geometrical works are directed to the measurement of curvilinear areas and volumes; and Archimedes employs a method which is a development of Eudoxus’s method of exhaustion. Eudoxus apparently approached the figure to be measured from below only, i. e. by means of figures successively inscribed to it. Archimedes approaches it from both sides by successively inscribing figures and circumscribing others also, thereby compressing them, as it were, until they coincide as nearly as we please with the figure to be measured. In many cases his procedure is, when the analytical equivalents are set down, seen to amount to real integration; this is so with his investigation of the areas of a parabolic segment and a spiral, the surface and volume of a sphere, and the volume of any segments of the conoids and spheroids.
[124] The newly-discovered Method is especially interesting as showing how Archimedes originally obtained his results; this was by a clever mechanical method of (theoretically) weighing infinitesimal elements of the figure to be measured against elements of another figure the area or content of which (as the case may be) is known; it amounts to an avoidance of integration. Archimedes, however, would only admit that the mechanical method is useful for finding results; he did not consider them proved until they were established geometrically.
In the Measurement of a Circle, after proving by exhaustion that the area of a circle is equal to a right-angled triangle with the perpendicular sides equal respectively to the radius and the circumference of the circle, Archimedes finds, by sheer calculation, upper and lower limits to the ratio of the circumference of a circle to its diameter (what we call π). This he does by inscribing and circumscribing regular polygons of 96 sides and calculating approximately their respective perimeters. He begins by assuming as known certain approximate values for √3, namely 1351/780 > √3 > 265/153, and his calculations involve approximating to the square roots of several large numbers (up to seven digits). The text only gives the results, but it is evident that the extraction of square roots presented no difficulty, notwithstanding the comparative inconvenience of the alphabetic system of numerals. The result obtained is well known, namely 3-1/7 > π > 3-10/71.
The Plane Equilibriums is the first scientific treatise on the first principles of mechanics, which are established by pure geometry. The most important result established in Book I is the principle of the lever. This was known to Plato and Aristotle, but they had no real proof. The Aristotelian Mechanics merely ‘refers’ the lever ‘to the circle’, asserting that the force which acts at the greater distance from the fulcrum moves the system more easily because it describes a greater circle. Archimedes also finds the centre of gravity[125] of a parallelogram, a triangle, a trapezium and finally (in Book II) of a parabolic segment and of a portion of it cut off by a straight line parallel to the base.
The Sandreckoner is remarkable for the development in it of a system for expressing very large numbers by orders and periods based on powers of myriad-myriads (10,000²). It also contains the important reference to the heliocentric theory of the universe put forward by Aristarchus of Samos in a book of ‘hypotheses’, as well as historical details of previous attempts to measure the size of the earth and to give the sizes and distances of the sun and moon.
Lastly, Archimedes invented the whole science of hydrostatics. Beginning the treatise On Floating Bodies with an assumption about uniform pressure in a fluid, he first proves that the surface of a fluid at rest is a sphere with its centre at the centre of the earth. Other propositions show that, if a solid floats in a fluid, the weight of the solid is equal to that of the fluid displaced, and, if a solid heavier than a fluid is weighed in it, it will be lighter than its true weight by the weight of the fluid displaced. Then, after a second assumption that bodies which are forced upwards in a fluid are forced upwards along the perpendiculars to the surface which pass through their centres of gravity, Archimedes deals with the position of rest and stability of a segment of a sphere floating in a fluid with its base entirely above or entirely below the surface. Book II is an extraordinary tour de force, investigating fully all the positions of rest and stability of a right segment of a paraboloid floating in a fluid according (1) to the relation between the axis of the solid and the parameter of the generating parabola, and (2) to the specific gravity of the solid in relation to the fluid; the term ‘specific gravity’ is not used, but the idea is fully expressed in other words.
Almost contemporary with Archimedes was Eratosthenes of Cyrene, to whom Archimedes dedicated the Method; the [126] preface to this work shows that Archimedes thought highly of his mathematical ability. He was indeed recognized by his contemporaries as a man of great distinction in all branches, though the names Beta and Pentathlos[4] applied to him indicate that he just fell below the first rank in each subject. Ptolemy Euergetes appointed him to be tutor to his son (Philopator), and he became librarian at Alexandria; he recognized his obligation to Ptolemy by erecting a column with a graceful epigram. In this epigram he referred to the earlier solutions of the problem of duplicating the cube or finding the two mean proportionals, and advocated his own in preference, because it would give any number of means; on the column was fixed a bronze representation of his appliance, a frame with right-angled triangles (or rectangles) movable along two parallel grooves and over one another, together with a condensed proof. The Platonicus of Eratosthenes evidently dealt with the fundamental notions of mathematics in connexion with Plato’s philosophy, and seems to have begun with the story of the origin of the duplication problem.
The most famous achievement of Eratosthenes was his measurement of the earth. Archimedes quotes an earlier measurement which made the circumference of the earth 300,000 stades. Eratosthenes improved upon this. He observed that at the summer solstice at Syene, at noon, the sun cast no shadow, while at the same moment the upright gnomon at Alexandria cast a shadow corresponding to an angle between the gnomon and the sun’s rays of 1/50th of four right angles. The distance between Syene and Alexandria being known to be 5,000 stades, this gave for the circumference of the earth 250,000 stades, which Eratosthenes seems later, for some reason, to have changed to 252,000 stades. On the [127] most probable assumption as to the length of the stade used, the 252,000 stades give about 7,850 miles, only 50 miles less than the true polar diameter.
In the work On the Measurement of the Earth Eratosthenes is said to have discussed other astronomical matters, the distance of the tropic and polar circles, the sizes and distances of the sun and moon, total and partial eclipses, &c. Besides other works on astronomy and chronology, Eratosthenes wrote a Geographica in three books, in which he first gave a history of geography up to date and then passed on to mathematical geography, the spherical shape of the earth, &c., &c.
Apollonius of Perga was with justice called by his contemporaries the ‘Great Geometer’, on the strength of his great treatise, the Conics. He is mentioned as a famous astronomer of the reign of Ptolemy Euergetes (247-222 B. C.); and he dedicated the fourth and later Books of the Conics to King Attalus I of Pergamum (241-197 B. C.).
The Conics, a colossal work, originally in eight Books, survives as to the first four Books in Greek and as to three more in Arabic, the eighth being lost. From Apollonius’s prefaces we can judge of the relation of his work to Euclid’s Conics, the content of which answered to the first three Books of Apollonius. Although Euclid knew that an ellipse could be otherwise produced, e. g. as an oblique section of a right cylinder, there is no doubt that he produced all three conics from right cones like his predecessors. Apollonius, however, obtains them in the most general way by cutting any oblique cone, and his original axes of reference, a diameter and the tangent at its extremity, are in general oblique; the fundamental properties are found with reference to these axes by ‘application of areas’, the three varieties of which, application (παραβολη), application with an excess (ὑπερβολη) and application with a deficiency (ελλειψις), give the properties of the three curves respectively and account for the names[128] parabola, hyperbola, and ellipse, by which Apollonius called them for the first time. The principal axes only appear, as a particular case, after it has been shown that the curves have a like property when referred to any other diameter and the tangent at its extremity, instead of those arising out of the original construction. The first four Books constitute what Apollonius calls an elementary introduction; the remaining Books are specialized investigations, the most important being Book V (on normals) and Book VII (mainly on conjugate diameters). Normals are treated, not in connexion with tangents, but as minimum or maximum straight lines drawn to the curves from different points or classes of points. Apollonius discusses such questions as the number of normals that can be drawn from one point (according to its position) and the construction of all such normals. Certain propositions of great difficulty enable us to deduce quite easily the Cartesian equations to the evolutes of the three conics.
Several other works of Apollonius are described by Pappus as forming part of the ‘Treasury of Analysis’. All are lost except the Sectio Rationis in two Books, which survives in Arabic and was published in a Latin translation by Halley in 1706. It deals with all possible cases of the general problem ‘given two straight lines either parallel or intersecting, and a fixed point on each, to draw through any given point a straight line which shall cut off intercepts from the two lines (measured from the fixed points) bearing a given ratio to one another’. The lost treatise Sectio Spatii dealt similarly with the like problem in which the intercepts cut off have to contain a given rectangle.
The other treatises included in Pappus’s account are (1) On Determinate Section; (2) Contacts or Tangencies, Book II of which is entirely devoted to the problem of drawing a circle to touch three given circles (Apollonius’s solution can, with the aid of Pappus’s auxiliary propositions, be satisfactorily [129] restored); (3) Plane Loci, i. e. loci which are straight lines or circles; (4) Νευσεις, Inclinationes (the general problem called a νευσις being to insert between two lines, straight or curved, a straight line of given length verging to a given point, i. e. so that, if produced, it passes through the point, Apollonius restricted himself to cases which could be solved by ‘plane’ methods, i. e. by the straight line and circle only).
Apollonius is also said to have written (5) a Comparison of the dodecahedron with the icosahedron (inscribed in the same sphere), in which he proved that their surfaces are in the same ratio as their volumes; (6) On the cochlias or cylindrical helix; (7) a ‘General Treatise’, which apparently dealt with the fundamental assumptions, &c., of elementary geometry; (8) a work on unordered irrationals, i. e. irrationals of more complicated form than those of Eucl. Book X; (9) On the burning-mirror, dealing with spherical mirrors and probably with mirrors of parabolic section also; (10) ωκυτοκιον (‘quick delivery’). In the last-named work Apollonius found an approximation to π closer than that in Archimedes’s Measurement of a Circle; and possibly the book also contained Apollonius’s exposition of his notation for large numbers according to ‘tetrads’ (successive powers of the myriad).
In astronomy Apollonius is said to have made special researches regarding the moon, and to have been called ε (Epsilon) because the form of that letter is associated with the moon. He was also a master of the theory of epicycles and eccentrics.
With Archimedes and Apollonius Greek geometry reached its culminating point; indeed, without some more elastic notation and machinery such as algebra provides, geometry was practically at the end of its resources. For some time, however, there were capable geometers who kept up the tradition, filling in details, devising alternative solutions of problems, or discovering new curves for use or investigation.
[130] Nicomedes, probably intermediate in date between Eratosthenes and Apollonius, was the inventor of the conchoid or cochloid, of which, according to Pappus, there were three varieties. Diocles (about the end of the second century B. C.) is known as the discoverer of the cissoid which was used for duplicating the cube. He also wrote a book περι πυρειων, On burning-mirrors, which probably discussed, among other forms of mirror, surfaces of parabolic or elliptic section, and used the focal properties of the two conics; it was in this work that Diocles gave an independent and clever solution (by means of an ellipse and a rectangular hyperbola) of Archimedes’s problem of cutting a sphere into two segments in a given ratio. Dionysodorus gave a solution by means of conics of the auxiliary cubic equation to which Archimedes reduced this problem; he also found the solid content of a tore or anchor-ring.
Perseus is known as the discoverer and investigator of the spiric sections, i. e. certain sections of the σπειρα, one variety of which is the tore. The spire is generated by the revolution of a circle about a straight line in its plane, which straight line may either be external to the circle (in which case the figure produced is the tore), or may cut or touch the circle.
Zenodorus was the author of a treatise on Isometric figures, the problem in which was to compare the content of different figures, plane or solid, having equal contours or surfaces respectively.
Hypsicles (second half of second century B. C.) wrote what became known as ‘Book XIV’ of the Elements containing supplementary propositions on the regular solids (partly drawn from Aristaeus and Apollonius); he seems also to have written on polygonal numbers. A mediocre astronomical work (Αναφορικος) attributed to him is the first Greek book in which we find the division of the zodiac circle into 360 parts or degrees.
Posidonius the Stoic (about 135-51 B. C.) wrote on geography [131] and astronomy under the titles On the Ocean and περι μετεωρων. He made a new but faulty calculation of the circumference of the earth (240,000 stades). Per contra, in a separate tract on the size of the sun (in refutation of the Epicurean view that it is as big as it looks), he made assumptions (partly guesswork) which give for the diameter of the sun a figure of 3,000,000 stades (39-1/4 times the diameter of the earth), a result much nearer the truth than those obtained by Aristarchus, Hipparchus, and Ptolemy. In elementary geometry Posidonius gave certain definitions (notably of parallels, based on the idea of equidistance).
Geminus of Rhodes, a pupil of Posidonius, wrote (about 70 B. C.) an encyclopaedic work on the classification and content of mathematics, including the history of each subject, from which Proclus and others have preserved notable extracts. An-Nairīzī (an Arabian commentator on Euclid) reproduces an attempt by one ‘Aganis’, who appears to be Geminus, to prove the parallel-postulate.
But from this time onwards the study of higher geometry (except sphaeric) seems to have languished, until that admirable mathematician, Pappus, arose (towards the end of the third century A. D.) to revive interest in the subject. From the way in which, in his great Collection, Pappus thinks it necessary to describe in detail the contents of the classical works belonging to the ‘Treasury of Analysis’ we gather that by his time many of them had been lost or forgotten, and that he aimed at nothing less than re-establishing geometry at its former level. No one could have been better qualified for the task. Presumably such interest as Pappus was able to arouse soon flickered out; but his Collection remains, after the original works of the great mathematicians, the most comprehensive and valuable of all our sources, being a handbook or guide to Greek geometry and covering practically the whole field. Among the original things in Pappus’s Collection is an enunciation[132] which amounts to an anticipation of what is known as Guldin’s Theorem.
It remains to speak of three subjects, trigonometry (represented by Hipparchus, Menelaus, and Ptolemy), mensuration (in Heron of Alexandria), and algebra (Diophantus).
Although, in a sense, the beginnings of trigonometry go back to Archimedes (Measurement of a Circle), Hipparchus was the first person who can be proved to have used trigonometry systematically. Hipparchus, the greatest astronomer of antiquity, whose observations were made between 161 and 126 B. C., discovered the precession of the equinoxes, calculated the mean lunar month at 29 days, 12 hours, 44 minutes, 2½ seconds (which differs by less than a second from the present accepted figure!), made more correct estimates of the sizes and distances of the sun and moon, introduced great improvements in the instruments used for observations, and compiled a catalogue of some 850 stars; he seems to have been the first to state the position of these stars in terms of latitude and longitude (in relation to the ecliptic). He wrote a treatise in twelve Books on Chords in a Circle, equivalent to a table of trigonometrical sines. For calculating arcs in astronomy from other arcs given by means of tables he used propositions in spherical trigonometry.
The Sphaerica of Theodosius of Bithynia (written, say, 20 B. C.) contains no trigonometry. It is otherwise with the Sphaerica of Menelaus (fl. A. D. 100) extant in Arabic; Book I of this work contains propositions about spherical triangles corresponding to the main propositions of Euclid about plane triangles (e.g. congruence theorems and the proposition that in a spherical triangle the three angles are together greater than two right angles), while Book III contains genuine spherical trigonometry, consisting of ‘Menelaus’s Theorem’ with reference to the sphere and deductions therefrom.
Ptolemy’s great work, the Syntaxis, written about A. D. 150[133] and originally called Μαθηματικη συνταξις, came to be known as Μεγαλη συνταξις; the Arabs made up from the superlative μεγιστος the word al-Majisti which became Almagest.
Book I, containing the necessary preliminaries to the study of the Ptolemaic system, gives a Table of Chords in a circle subtended by angles at the centre of ½° increasing by half-degrees to 180°. The circle is divided into 360 μοιραι, parts or degrees, and the diameter into 120 parts (τμηματα); the chords are given in terms of the latter with sexagesimal fractions (e. g. the chord subtended by an angle of 120° is 103p 53′ 23″). The Table of Chords is equivalent to a table of the sines of the halves of the angles in the table, for, if (crd. 2 α) represents the chord subtended by an angle of 2 α (crd. 2 α)/120 = sin α. Ptolemy first gives the minimum number of geometrical propositions required for the calculation of the chords. The first of these finds (crd. 36°) and (crd. 72°) from the geometry of the inscribed pentagon and decagon; the second (‘Ptolemy’s Theorem’ about a quadrilateral in a circle) is equivalent to the formula for sin (θ-φ), the third to that for sin ½ θ. From (crd. 72°) and (crd. 60°) Ptolemy, by using these propositions successively, deduces (crd. 1½°) and (crd. ¾°), from which he obtains (crd. 1°) by a clever interpolation. To complete the table he only needs his fourth proposition, which is equivalent to the formula for cos (θ+φ).
Ptolemy wrote other minor astronomical works, most of which survive in Greek or Arabic, an Optics in five Books (four Books almost complete were translated into Latin in the twelfth century), and an attempted proof of the parallel-postulate which is reproduced by Proclus.
Heron of Alexandria (date uncertain; he may have lived as late as the third century A. D.) was an almost encyclopaedic writer on mathematical and physical subjects. He aimed at practical utility rather than theoretical completeness; hence, apart from the interesting collection of Definitions which has[134] come down under his name, and his commentary on Euclid which is represented only by extracts in Proclus and an-Nairīzī, his geometry is mostly mensuration in the shape of numerical examples worked out. As these could be indefinitely multiplied, there was a temptation to add to them and to use Heron’s name. However much of the separate works edited by Hultsch (the Geometrica, Geodaesia, Stereometrica, Mensurae, Liber geëponicus) is genuine, we must now regard as more authoritative the genuine Metrica discovered at Constantinople in 1896 and edited by H. Schöne in 1903 (Teubner). Book I on the measurement of areas is specially interesting for (1) its statement of the formula used by Heron for finding approximations to surds, (2) the elegant geometrical proof of the formula for the area of a triangle Δ = √{s (s-a) (s-b) (s-c)}, a formula now known to be due to Archimedes, (3) an allusion to limits to the value of π found by Archimedes and more exact than the 3-1/7 and 3-10/71 obtained in the Measurement of a Circle.
Book I of the Metrica calculates the areas of triangles, quadrilaterals, the regular polygons up to the dodecagon (the areas even of the heptagon, enneagon, and hendecagon are approximately evaluated), the circle and a segment of it, the ellipse, a parabolic segment, and the surfaces of a cylinder, a right cone, a sphere and a segment thereof. Book II deals with the measurement of solids, the cylinder, prisms, pyramids and cones and frusta thereof, the sphere and a segment of it, the anchor-ring or tore, the five regular solids, and finally the two special solids of Archimedes’s Method; full use is made of all Archimedes’s results. Book III is on the division of figures. The plane portion is much on the lines of Euclid’s Divisions (of figures). The solids divided in given ratios are the sphere, the pyramid, the cone and a frustum thereof. Incidentally Heron shows how he obtained an approximation to the cube root of a non-cube number (100). Quadratic equations are solved by Heron by a regular rule not unlike our[135] method, and the Geometrica contains two interesting indeterminate problems.
Heron also wrote Pneumatica (where the reader will find such things as siphons, Heron’s Fountain, penny-in-the-slot machines, a fire-engine, a water-organ, and many arrangements employing the force of steam), Automaton-making, Belopoeïca (on engines of war), Catoptrica, and Mechanics. The Mechanics has been edited from the Arabic; it is (except for considerable fragments) lost in Greek. It deals with the puzzle of ‘Aristotle’s Wheel’, the parallelogram of velocities, definitions of, and problems on, the centre of gravity, the distribution of weights between several supports, the five mechanical powers, mechanics in daily life (queries and answers). Pappus covers much the same ground in Book VIII of his Collection.
We come, lastly, to Algebra. Problems involving simple equations are found in the Papyrus Rhind, in the Epanthema of Thymaridas already referred to, and in the arithmetical epigrams in the Greek Anthology (Plato alludes to this class of problem in the Laws, 819 B, C); the Anthology even includes two cases of indeterminate equations of the first degree. The Pythagoreans gave general solutions in rational numbers of the equations x²+y²=z² and 2x²-y²=±1, which are indeterminate equations of the second degree.
The first to make systematic use of symbols in algebraical work was Diophantus of Alexandria (fl. about A. D. 250). He used (1) a sign for the unknown quantity, which he calls αριθμος, and compendia for its powers up to the sixth; (2) a sign (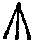 ) with the effect of our minus. The latter sign probably represents ΛΙ, an abbreviation for the root of the word λειπειν (to be wanting); the sign for αριθμος (
) with the effect of our minus. The latter sign probably represents ΛΙ, an abbreviation for the root of the word λειπειν (to be wanting); the sign for αριθμος (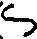 ) is most likely an abbreviation for the letters αρ; the compendia for the powers of the unknown are ΔΥ for δυναμις, the square, ΚΥ for κυβος, the cube, and so on. Diophantus shows that he solved quadratic equations by rule, like Heron. His Arithmetica, of[136] which six books only (out of thirteen) survive, contains a certain number of problems leading to simple equations, but is mostly devoted to indeterminate or semi-determinate analysis, mainly of the second degree. The collection is extraordinarily varied, and the devices resorted to are highly ingenious. The problems solved are such as the following (fractional as well as integral solutions being admitted): ‘Given a number, to find three others such that the sum of the three, or of any pair of them, together with the given number is a square’, ‘To find four numbers such that the square of the sum plus or minus any one of the numbers is a square’, ‘To find three numbers such that the product of any two plus or minus the sum of the three is a square’. Diophantus assumes as known certain theorems about numbers which are the sums of two and three squares respectively, and other propositions in the Theory of Numbers. He also wrote a book On Polygonal Numbers of which only a fragment survives.
) is most likely an abbreviation for the letters αρ; the compendia for the powers of the unknown are ΔΥ for δυναμις, the square, ΚΥ for κυβος, the cube, and so on. Diophantus shows that he solved quadratic equations by rule, like Heron. His Arithmetica, of[136] which six books only (out of thirteen) survive, contains a certain number of problems leading to simple equations, but is mostly devoted to indeterminate or semi-determinate analysis, mainly of the second degree. The collection is extraordinarily varied, and the devices resorted to are highly ingenious. The problems solved are such as the following (fractional as well as integral solutions being admitted): ‘Given a number, to find three others such that the sum of the three, or of any pair of them, together with the given number is a square’, ‘To find four numbers such that the square of the sum plus or minus any one of the numbers is a square’, ‘To find three numbers such that the product of any two plus or minus the sum of the three is a square’. Diophantus assumes as known certain theorems about numbers which are the sums of two and three squares respectively, and other propositions in the Theory of Numbers. He also wrote a book On Polygonal Numbers of which only a fragment survives.
With Pappus and Diophantus the list of original writers on mathematics comes to an end. After them came the commentators whose names only can be mentioned here. Theon of Alexandria, the editor of Euclid, lived towards the end of the fourth century A. D. To the fifth and sixth centuries belong Proclus, Simplicius, and Eutocius, to whom we can never be grateful enough for the precious fragments which they have preserved from works now lost, and particularly the History of Geometry and the History of Astronomy by Aristotle’s pupil Eudemus.
Such is the story of Greek mathematical science. If anything could enhance the marvel of it, it would be the consideration of the shortness of the time (about 350 years) within which the Greeks, starting from the very beginning, brought geometry to the point of performing operations equivalent to the integral calculus and, in the realm of astronomy, actually anticipated Copernicus.
T. L. Heath.
Footnotes
[1] Since this paper was first written Euclid, Book I, in the Greek, has been edited with a commentary by Sir Thomas Heath (Cambridge Press, 1920). It is full of interest and instruction.
[2] See my paper on ‘The Socratic Doctrine of the Soul’. Proceedings of the British Academy, 1915-16, pp. 235 sqq.
[3] In the case of the parabola, the base (as distinct from the ‘erect side’) of the rectangle is what is called the abscissa (Gk. αποτεμνομενη, ‘cut off’) of the ordinate, and the rectangle itself is equal to the square on the ordinate. In the case of the central conics, the base of the rectangle is ‘the transverse side of the figure’ or the transverse diameter (the diameter of reference), and the rectangle is equal to the square on the diameter conjugate to the diameter of reference.
[4] This word primarily means an all-round athlete, a winner in all five of the sports constituting the πενταθλον, namely jumping, discus-throwing, running, wrestling, and boxing (or javelin-throwing).
[5] επι δε τουτοις Πυθαγορας την περι αυτην φιλοσοφιαν εις σχημα παιδειας ελευθερου μετεστησεν. {epi de toutois Pythagoras tên peri autên philosophian eis schêma paideias eleutherou metestêsen.} Procli Comment. Euclidis lib. I, Prolegom. II (p. 65, ed. Friedlein).
[6] The word Biology was introduced by Gottfried Reinhold Treviranus (1776-1837) in his Biologie oder die Philosophie der lebenden Natur, 6 vols., Göttingen, 1802-22, and was adopted by J.-B. de Lamarck (1744-1829) in his Hydrogéologie, Paris, 1802. It is probable that the first English use of the word in its modern sense is by Sir William Lawrence (1783-1867) in his work On the Physiology, Zoology, and Natural History of Man, London, 1819; there are earlier English uses of the word, however, contrasted with biography.
[7] The remains of Alcmaeon are given in H. Diel’s Die Fragmente der Vorsokratiker, Berlin, 1903, p. 103. Alcmaeon is considered in the companion chapter on Greek Medicine.
[8] Especially the περι γυναικειης φυσιος, On the nature of woman, and the περι γυναικειων, On the diseases of women.
[9] περι ἑβδομαδων. The Greek text is lost. We have, however, an early and barbarous Latin translation, and there has recently been printed an Arabic commentary. G. Bergstrasser, Pseudogaleni in Hippocratis de septimanis commentarium ab Hunnino Q. F. arabice versum, Leipzig, 1914.
[10] περι νουσων δ.
[11] περι καρδιης.
[12] Especially in the περι γονης.
[13] The three works περι γονης, περι φυσιος παιδιου, περι νουσων δ, On generation, on the nature of the embryo, on diseases, book IV, form really one treatise on generation.
[14] περι φυσιος παιδιου, On the nature of the embryo, § 13. The same experience is described in the περι σαρκων, On the muscles.
[15] περι φυσιος παιδιου, On the nature of the embryo, § 29.
[16] περι φυσιος παιδιου, On the nature of the embryo, § 22.
[17] Ibid. § 23.
[18] It is possible that Theophrastus derived the word pericarp from Aristotle. Cp. De anima, ii. 1, 412 b 2. In the passage το φυλλον περικαρπιου σκεπασμα, το δε περικαρπιον καρπου, in the De anima the word does not, however, seem to have the full technical force that Theophrastus gives to it.
[19] Historia plantarum, i. 2, vi.
[20] Ibid. i. 1, iv.
[21] Historia plantarum, ii. 1, i.
[22] Historia plantarum, viii. 1, i.
[23] Nathaniel Highmore, A History of Generation, London, 1651.
[24] Marcello Malpighi, Anatome plantarum, London, 1675.
[25] Nehemiah Grew, Anatomy of Vegetables begun, London, 1672.
[26] Pliny, Naturalis historia, xiii. 4.
[27] The curious word ολυνθαζειν, here translated to use the wild fig, is from ολυνθος, a kind of wild fig which seldom ripens. The special meaning here given to the word is explained in another work of Theophrastus, De causis plantarum, ii. 9, xv. After describing caprification in figs, he says το δε επι των φοινικων συμβαινον ου ταυτον μεν, εχει δε τινα ὁμοιοτητα τουτω δι’ ὁ καλουσιν ολυνθαζειν αυτους {to de epi tôn phoinikôn symbainon ou tauton men, echei de tina homoiotêta toutô di’ ho kalousin olynthazein autous} ‘The same thing is not done with dates, but something analogous to it, whence this is called ολυνθαζειν’.
[28] Historia plantarum, ii. 8, iv.
[29] Herodotus i. 193.
[30] Historia plantarum, ii. 8, i.
[31] Ibid. ii. 8, ii.
[32] Historia plantarum, ii. 8, iv.
[33] Ibid. i. 1, ix.
[34] Ibid. iii. 18, x.
[35] De causis plantarum, ii. 23.
[36] Historia plantarum, i. 13, iii.
[37] See the companion chapter on Greek Medicine.
[38] The surviving fragments of the works of Crateuas have recently been printed by M. Wellmann as an appendix to the text of Dioscorides, De materia medica, 3 vols., Berlin, 1906-17, iii. pp. 144-6. The source and fate of his plant drawings are discussed in the same author’s Krateuas, Berlin, 1897.
[39] The manuscript in question is Med. Graec. 1 at what was the Royal Library at Vienna. It is known as the Constantinopolitanus. After the war it was taken to St. Mark’s at Venice, but either has been or is about to be restored to Vienna. A facsimile of this grand manuscript was published by Sijthoff, Leyden, 1906.
[40] The lady in question was Juliana Anicia, daughter of Anicius Olybrius, Emperor of the West in 472, and his wife Placidia, daughter of Valentinian III. Juliana was betrothed in 479 by the Eastern Emperor Zeno to Theodoric the Ostrogoth, but was married, probably in 487 when the manuscript was presented to her, to Areobindus, a high military officer under the Byzantine Emperor Anastasius.
[41] The importance of this manuscript as well as the position of Dioscorides as medical botanist is discussed by Charles Singer in an article ‘Greek Biology and the Rise of Modern Biology’, Studies in the History and Method of Science, vol. ii, Oxford, 1921.
[42] This manuscript is at the University Library at Leyden, where it is numbered Voss Q 9.
[43] A good instance of Galen’s teleological point of view is afforded by his classical description of the hand in the περι χρειας των εν ανθρωπου σωματι μοριων, On the uses of the parts of the body of man, i. 1. This passage is available in English in a tract by Thomas Bellott, London, 1840.
[44] The early European translations from the Arabic are tabulated with unparalleled learning by M. Steinschneider, ‘Die Europäischen Uebersetzungen aus dem Arabischen bis Mitte des 17. Jahrhunderts’, in the Sitzungsberichte der kais. Akad. der Wissenschaften in Wien, cxlix and cli, Vienna, 1904 and 1905.
[45] C. H. Haskins, ‘The reception of Arabic science in England,’ English Historical Review, London, 1915, p. 56.
[46] Roger Bacon, Opus majus, edited by J. H. Bridges, 3 vols., London, 1897-1900. Vol. iii, p. 66.
[47] On the Aristotelian translations of Scott see A. H. Querfeld, Michael Scottus und seine Schrift, De secretis naturae, Leipzig, 1919; and C. H. Haskins, ‘Michael Scot and Frederick II’ in Isis, ii. 250, Brussels, 1922.
[48] J. G. Schneider, Aristotelis de animalibus historiae, Leipzig, 1811, p. cxxvi. L. Dittmeyer, Guilelmi Moerbekensis translatio commentationis Aristotelicae de generatione animalium, Dillingen, 1915. L. Dittmeyer, De animalibus historia, Leipzig, 1907.
[49] The subject of the Latin translations of Aristotle is traversed by A. and C. Jourdain, Recherches critiques sur l’âge des traductions latines d’Aristote, 2nd ed., Paris, 1843; M. Grabmann, Forschungen uber die lateinischen Aristoteles Ubersetzungen des XIII. Jahrhunderts, Münster i/W., 1916; and F. Wüstenfeld, Die Ubersetzungen arabischer Werke in das Lateinische seit dem XI. Jahrhundert, Göttingen, 1877.
[50] The enormous De Animalibus of Albert of Cologne is now available in an edition by H. Stadler, Albertus Magnus De Animalibus Libri XXVI nach der cölner Urschrift, 2 vols., Münster i/W., 1916-21. The quotation is translated from vol. i, pp. 465-6.
[51] Conrad’s work is conveniently edited by H. Schultz, Das Buch der Natur von Conrad von Megenberg, die erste Naturgeschichte in deutscher Sprache, in Neu-Hochdeutsche Sprache bearbeitet, Greifswald, 1897. Conrad’s work is based on that of Thomas of Cantimpré (1201-70).
[52] Hieronimo Fabrizio of Acquapendente, De formato foetu, Padua, 1604.
[53] William Harvey, Exercitationes de generatione animalium, London, 1651.
[54] Karl Ernst von Baer, Ueber die Entwickelungsgeschichte der Thiere, Königsberg, 1828-37.
[55] The works of Herophilus are lost. This fine passage has been preserved for us by Sextus Empiricus, a third-century physician, in his προς τοις μαθηματικους αιτιρρητικοι, which is in essence an attack on all positive philosophy. It is an entertaining fact that we should have to go to such a work for remains of the greatest anatomist of antiquity. The passage is in the section directed against ethical writers, xi. 50.
[56] The word φυσικος, though it passed over into Latin (Cicero) with the meaning naturalist, acquired the connotation of sorcerer among the later Greek writers. Perhaps the word physicianus was introduced to make a distinction from the charm-mongering physicus. In later Latin physicus and medicus are almost always interchangeable.
[57] This fragment has been published in vol. iii, part 1, of the Supplementum Aristotelicum by H. Diels as Anonymi Londinensis ex Aristotelis Iatricis Menonis et Aliis Medicis Eclogae, Berlin, 1893. See also H. Bekh and F. Spät, Anonymus Londinensis, Auszuge eines Unbekannten aus Aristoteles-Menons Handbuch der Medizin, Berlin, 1896.
[58] As we go to press there appears a preliminary account of the very remarkable Edwin Smith papyrus, see J. H. Breasted in Recueil d’études egyptologiques dédiées à la mémoire de Champollion, Paris 1922, and New York Historical Society Bulletin, 1922.
[59] It is tempting, also, to connect the Asclepian snake cult with the prominence of the serpent in Minoan religion.
[60] This word pronoia, as Galen explains (εις το Ἱπποκρατους προγνωστικον, K. xviii, B. p. 10), is not used in the philosophic sense, as when we ask whether the universe was made by chance or by pronoia, nor is it used quite in the modern sense of prognosis, though it includes that too. Pronoia in Hippocrates means knowing things about a patient before you are told them. See E. T. Withington, ‘Some Greek medical terms with reference to Luke and Liddell and Scott,’ Proceedings of the Royal Society of Medicine (Section of the History of Medicine), xiii, p. 124, London, 1920.
[61] Prognostics 1.
[62] There is a discussion of the relation of the Asclepiadae to temple practice in an article by E. T. Withington, ‘The Asclepiadae and the Priest of Asclepius,’ in Studies in the History and Method of Science, edited by Charles Singer, vol. ii, Oxford, 1921.
[63] The works of Anaximenes are lost. This phrase of his, however, is preserved by the later writer Aetios.
[64] For the work of these physicians see especially M. Wellmann, Fragmentsammlung der griechischen Aerzte, Bd. I, Berlin, 1901.
[65] Galen, περι ανατομικων εγχειρησεων, On anatomical preparations, § 1, K. II, p. 282.
[66] Historia animalium, iii. 3, where it is ascribed to Polybus. The same passage is, however, repeated twice in the Hippocratic writings, viz. in the περι φυσιος ανθρωπου, On the nature of man, Littré, vi. 58, and in the περι οστεων φυσιος, On the nature of bones, Littré, ix. 174.
[67] Παραγγελιαι, § 6.
[68] See Fig. 1.
[69] Translation by Professor Arthur Platt.
[70] It must, however, be admitted that in the Hippocratic collection are breaches of the oath, e. g. in the induction of abortion related in περι φυσιος παιδιου. There is evidence, however, that the author of this work was not a medical practitioner.
[71] Rome Urbinas 64, fo. 116.
[72] Kühlewein, i. 79, regards this as an interpolated passage.
[73] Littré, ii. 112; Kühlewein, i. 79. The texts vary: Kühlewein is followed except in the last sentence.
[74] Περι τεχνης, § 3.
[75] Περι νουσων α', § 6.
[76] A reference to dissection in the περι αρθρων, On the joints, § 1, appears to the present writer to be of Alexandrian date.
[77] They are to be found as an Appendix to Books I and III of the Epidemics and embedded in Book III.
[78] John Cheyne (1777-1836) described this type of respiration in the Dublin Hospital Reports, 1818, ii, p. 216. An extreme case of this condition had been described by Cheyne’s namesake George Cheyne (1671-1743) as the famous ‘Case of the Hon. Col. Townshend’ in his English Malady, London, 1733. William Stokes (1804-78) published his account of Cheyne-Stokes breathing in the Dublin Quarterly Journal of the Medical Sciences, 1846, ii, p. 73.
[79] The Epidaurian inscriptions are given by M. Fraenkel in the Corpus Inscriptionum Graecarum IV, 951-6, and are discussed by Mary Hamilton (Mrs. Guy Dickins), Incubation, St. Andrews, 1906, from whose translation I have quoted. Further inscriptions are given by Cavvadias in the Archaiologike Ephemeris, 1918, p. 155 (issued 1921).
[80] We are almost told as much in the apocryphal Gospel of Nicodemus, § 1, a work probably composed about the end of the fourth century.
[81] Astley Paston Cooper, Treatise on Dislocations and Fractures of the Joints, London, 1822, and Observations on Fractures of the Neck and the Thighbone, &c., London, 1823.
[82] This famous manuscript is known as Laurentian, Plutarch 74, 7, and its figures have been reproduced by H. Schöne, Apollonius von Kitium, Leipzig, 1896.
[83] The first lines are the source of the famous lines in Goethe’s Faust:
‘Ach Gott! die Kunst ist lang Und kurz ist unser Leben, Mir wird bei meinem kritischen Bestreben Doch oft um Kopf und Busen bang.’
[84] The extreme of treatment refers in the original to the extreme restriction of diet, ες ακριβειην, but the meaning of the Aphorism has always been taken as more generalized.
[85] The ancients knew almost nothing of infection as applied specifically to disease. All early peoples—including Greeks and Romans—believed in the transmission of qualities from object to object. Thus purity and impurity and good and bad luck were infections, and diseases were held to be infections in that sense. But there is little evidence in the belief of the special infectivity of disease as such in antiquity. Some few diseases are, however, unequivocally referred to as infectious in a limited number of passages, e. g. ophthalmia, scabies, and phthisis in the περι διαφορας πυρετων, On the differentiae of fevers, K. vii, p. 279. The references to infection in antiquity are detailed by C. and D. Singer, ‘The scientific position of Girolamo Fracastoro’, Annals of Medical History, vol. i, New York, 1917.
[86] K. F. H. Marx, Herophilus, ein Beitrag zur Geschichte der Medizin, Karlsruhe, 1838.
[87] Galen, περι ανατομικων εγχειρησεων, On anatomical preparations, ix. 5 (last sentence).
[88] Galen, περι φλεβων και αρτηριων ανατομης, On the anatomy of veins and arteries, i.
[89] The quotation is from chapter xxxiii, line 44 of the Anonymus Londinensis. H. Diels, Anonymus Londinensis in the Supplementum Aristotelicum, vol. iii, pars 1, Berlin, 1893.
[90] Sanctorio Santorio, Oratio in archilyceo patavino anno 1612 habita; de medicina statica aphorismi. Venice, 1614.
[91] This is the only passage of Hegetor’s writing that has survived. It has been preserved in the work of Apollonius of Citium.
[92] Leyden Voss 4° 9* of the sixth century is a fragment of this work.
[93] V. Rose, Sorani Ephesii vetus translatio Latina cum additis Graeci textus reliquiis, Leipzig, 1882; F. Weindler, Geschichte der gynäkologisch-anatomischen Abbildung, Dresden, 1908.
[94] The discovery and attribution of these figures is the work of K. Sudhoff. A bibliography of his writings on the subject will be found in a ‘Study in Early Renaissance Anatomy’ in C. Singer’s Studies in the History and Method of Science, vol. i, Oxford, 1917.
[95] First Latin edition Venice, 1552; first Greek edition Paris, 1554.
[96] e. g. περι κρασεως και δυναμεως των ἁπαντων φαρμακων and the φαρμακα.
[97] e. g. De dinamidiis Galeni, Secreta Hippocratis and many astrological tracts.
[98] Dissection of animals was practised at Salerno as early as the eleventh century.
[99] The sources of the anatomical knowledge of the Middle Ages are discussed in detail in the following works: R. R. von Töply, Studien zur Geschichte der Anatomie im Mittelalter, Vienna, 1898; K. Sudhoff, Tradition und Naturbeobachtung, Leipzig, 1907; and also numerous articles in the Archiv für Geschichte der Medizin und Naturwissenschaften; Charles Singer, ‘A Study in Early Renaissance Anatomy’, in Studies in the History and Method of Science, vol. i, Oxford, 1917.
[100] Benivieni’s notes were published posthumously. Some of the spurious Greek works of the Hippocratic collection have also case notes.
[101] Tusc. 1. 1. 2.
[102] Inst. Or. I. 1. 12.
[103] Goethe, Gespräche, 3. 387.
[104] Ibid., 3. 443.
[105] Wordsworth, Table-talk.
[106] Shelley, On the Manners of the Ancients.
[107] Mill, Dissertations, ii. 283 f.
[108] Macaulay, Life and Letters, i. 43.
[109] Homer, Iliad, vi. 466 ff. (with omissions: chiefly from the translation of Lang, Leaf, and Myers). It should be remembered that, of the three figures in this scene, the husband will be dead in a few days, while within a year the wife will be a slave and the child thrown from the city wall.
[110] Genesis xxi. 14 f.
[111] Iliad, xvi. 428 f.: ‘As vultures with crooked talons and curved beaks that upon some high crag fight, screaming loudly.’ Ibid. v. 770 f.: ‘As far as a man’s view ranges in the haze, as he sits on a point of outlook and gazes over the wine-dark sea, so far at a spring leap the loud-neighing horses of the gods.’
[112] Poetics, c. 23 (tr. Butcher).
[113] ‘Stranger, tell the Spartans that we lie here, obeying their words.’
[114] Phaedo, 118 B.
[115] fr. 95: ‘Star of evening, bringing all things that bright dawn has scattered, you bring the sheep, you bring the goat, you bring the child back to its mother.’
[116] Iliad, xxiv. 277 f. (with omissions).
[117] I have taken these quotations of Keats from Bradley, Oxford Lecture on Poetry, p. 238.
[118] Callimachus, Epigr. 20: ‘His father Philip laid here to rest his twelve-year old son, his high hope, Nicoteles.’
[119] Thuc. iv. 104, 105, 106 (tr. Jowett, mainly).
[120] The Greek Genius and its Meaning to us, pp. 74 ff.
[121] In these novels and in The Dynasts Mr. Hardy allows his personal views to depress one side of the scales: in his lesser novels he has often shown that he can hold the balance even. This distinction should be borne in mind in all the criticisms of his work, which I have ventured to make.
[122] Keats, Preface to Endymion.
[123] Hymn to Demeter, l. 2 ff. The translation is mainly from Pater, Greek Studies. ‘Whom, by the consent of far-seeing, deep-thundering Zeus, Aidoneus carried away, as she played with the deep-bosomed daughters of Ocean, gathering flowers in a meadow of soft grass and roses and crocus and fair violets and iris and hyacinths and the strange glory of the narcissus which the Earth, favouring the desire of Aidoneus, brought forth to snare the flower-like girl. A wonder it was to all, immortal gods and mortal men. A hundred blossoms grew up from the roots of it, and very sweet was its scent, and the broad sky above, and all the earth and the salt wave of the sea laughed to see it. She in wonder stretched out her two hands to take the lovely plaything: thereupon the wide-wayed earth opened in the Nysian plain and the king of the great nation of the dead sprang out with his immortal horses.’
[124] ll. 732 f. (tr. Murray).
[125] Vitruvius, De Architectura.
[126] Pliny the Elder, Historia Naturalis, xxxvi.
[127] Pausanias, Ἑλλαδος Περιηγησις.
[128] Sir Arthur Evans has drawn up an ingenious chronology of Early Minoan (2800-2200 B. C.), Middle Minoan (2200-1700 B. C.), and Late Minoan (1700-1200 B. C.). The evidence is almost entirely that of pottery discovered on the site. The whole question of the relations of Minoan to Mycenaean art, and of this archaic art to the earlier civilizations of Egypt and Chaldea, is very obscure and uncertain.
[129] The heraldic treatment of the lions is of Eastern origin. The Greeks had a tradition that the chieftains of Mycenae came from Lydia.
[130] Portions of these columns are now in the British Museum.
[131] The order, I may say for the uninitiated, means the complete ordonnance of the column, the architrave resting immediately on its capital, the frieze and the cornice. It is the final expression of the simple device of the post and lintel, of the beam resting on the heads of two or more posts; and there is little doubt that in its ultimate origin, the Order is the translation into stone of the details of a rudimentary wooden construction.
[132] Hellenistic Sculpture, by Guy Dickins, p. 85. The author, who wrote with something of the insight of the artist as well as the accurate knowledge of the scholar, died of wounds, on the Somme, in 1916.
[133] Vitruvius, iii. 1. The difficulty was, that if the triglyph was placed on the angle of the building (the practice of the Greeks) and the next triglyph was placed over the axis of the column, the metope (or panel) between these two triglyphs would be larger than the metopes between the triglyphs axial over the other columns. The Greeks solved it by reducing the width of the end intercolumniation, but later critics disliked this, and solved it by removing the end triglyph from the angle and placing it axial over the end column.
[134] Vitruvius gives this as the ‘aedes in antis’.
[135] Pro-style (colonnade in front).
[136] Amphipro-style (colonnade at both ends).
[137] Peripteral (single colonnade all round).
[138] Dipteral (double colonnade all round).
[139] Pseudo-dipteral (inner row of columns omitted).
[140] The Erechtheum was an exception.
[141] See Delphi, by Dr. Frederick Poulsen, p. 52. It is suggested that the Sacred Way was in existence before the shrines were built, and that its wanderings were necessitated by the gradients of the hillside. No sort of attempt, however, seems to have been made to correct this, or to treat it as an element of design.
[142] The Place Vendôme measures 450 ft. × 420 ft.; Grosvenor Square about 650 × 530; and Lincoln’s Inn Fields about 800 × 630, measured from wall to wall of buildings.
[143] Choisy, History of Architecture, vol. i, p. 298.
Transcriber’s Notes and Errata
Illustrations have been moved to the appropriate placed in the text.
The following typographical errors have been corrected.
| Page | Error | Correction |
| 218 | back | black |
| 424 | stedfast | steadfast |
The following words are found in hyphenated and unhyphenated forms in the text. The numbers of instances are given in parentheses.
| cuttle-fish (2) | cuttlefish (1) |
| fresh-water (1) | freshwater (1) |
| pre-occupation (4) | preoccupation (1) |
| preoccupations (1) | |
| re-arranging (1) | rearranging (1) |
| re-discovery (2) | rediscovery (3) |
| super-men (1) | supermen (1) |
| super-women (1) | superwomen (1) |
| text-book (5) | textbook (2) |
| text-books (2) | textbooks (3) |
|
Ancient Greece |
Medieval Greece / Byzantine Empire |
Modern Greece |
|---|---|---|
|
Science, Technology , Medicine , Warfare, , Biographies , Life , Cities/Places/Maps , Arts , Literature , Philosophy ,Olympics, Mythology , History , Images |
Science, Technology, Arts, , Warfare , Literature, Biographies, Icons, History |
Cities, Islands, Regions, Fauna/Flora ,Biographies , History , Warfare, Science/Technology, Literature, Music , Arts , Film/Actors , Sport , Fashion |
Retrieved from "http://en.wikipedia.org/"
All text is available under the terms of the GNU Free Documentation License

