.
Κάμψη είναι το αποτέλεσμα [1] κάθετων[2] δυνάμεων ή ροπών που ασκούνται σε ένα μακρόστενο σώμα. Όπως το σώμα τείνει να καμπυλωθεί στη μία πλευρά του προκαλείται θλίψη (συμπίεση) και στην άλλη εφελκυσμός (τράβηγμα).[3] Η κάμψη προκαλεί την παραμόρφωση ή ακόμα και την θραύση του σώματος.
Εσωτερικές τάσεις

Σχήμα 2. Ορθές τάσεις σε διατομή που κάμπτεται λόγω συγκεντρωμένης ροπής.

Σχήμα 3. Παραμόρφωση και τάση στη διατομή.
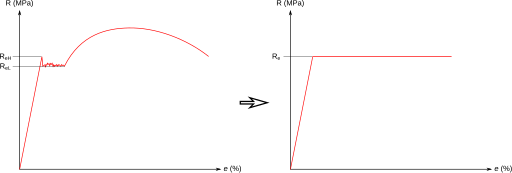
Σχήμα 4. Πραγματική και απλοποιημένη καμπύλη τάσης-παραμόρφωσης όλκιμου υλικού.
Ο τρίτος νόμος του Νεύτωνα προβλέπει ότι για να υπάρχει ισορροπία σε ένα σώμα πρέπει οι δυνάμεις που του ασκούνται να εξουδετερώνουν η μία την άλλη. Πρέπει συνεπώς, σε κάθε σημείο του καμπτόμενου σώματος, οι εξωτερικές δυνάμεις να εξουδετερώνονται από άλλες που αναπτύσσονται στο εσωτερικό του. Σε ένα σώμα σε κάμψη λοιπόν εμφανίζονται εσωτερικές τάσεις. Οι τάσεις που είναι κάθετες στη διατομή[4] του στοιχείου ονομάζονται ορθές. Οι εφελκυστικές θεωρούνται θετικές ενώ οι θλιπτικές αρνητικές. Η γραμμή όπου μηδενίζονται οι ορθές τάσεις ονομάζεται ουδέτερη γραμμή και χωρίζει τη διατομή στην εφελκυόμενη και τη θλιβόμενη περιοχή. Ο υπολογισμός των τάσεων είναι πολύ σημαντικός για τον έλεγχο της αντοχής του σώματος.
Θεωρία κάμψης Όιλερ-Μπερνούλι
Για τον υπολογισμό των ορθών τάσεων στη διατομή ενός στοιχείου πρέπει να ισχύουν οι εξής συνθήκες και παραδοχές:
Οι διατομές που πριν την κάμψη ήταν επίπεδες και κάθετες στον άξονα του στοιχείου παραμένουν επίπεδες και κάθετες ως προς τον παραμορφωμένο λόγω κάμψης άξονά του (παραδοχή Μπερνούλι).
Το υλικό είναι γραμμικά ελαστικό, ομογενές και ισότροπο. Γραμμικά ελαστικό ονομάζεται το υλικό που υπακούει στο νόμο του Χουκ, ενώ ισότροπο το υλικό που έχει την ίδια συμπεριφορά προς κάθε διεύθυνση.
Το στοιχείο είναι αρχικά ευθύγραμμο και σταθερής διατομής. Ισχύει και στην περίπτωση που οι μεταβολές της διατομής είναι μικρές και ομαλές κατά το μήκος.
Οι ορθές τάσεις δίνονται από τη σχέση: \( {\displaystyle {\sigma }={\frac {M_{(x)}z}{I_{z}}}} \).
Όπου:
\( {\displaystyle \ M_{(x)}} \): Η ροπή κάμψης στο σημείο \( {\displaystyle \ x} \).
\( {\displaystyle \ I_{z}} \) : Η ροπή αδράνειας ως προς τον κεντροβαρικό άξονα που είναι παράλληλος στον άξονα της κάμψης (σχήμα 6, άξονας y).
\( {\displaystyle \ z} \): απόσταση του σημείου με τάση σ από τον παραπάνω άξονα.
Απουσία αξονικών δυνάμεων ο άξονας της ροπής αδράνειας ταυτίζεται με τον ουδέτερο άξονα της διατομής.
H μέγιστη ορθή τάση \( {\displaystyle \ \sigma _{max}={\frac {M_{max}z_{max}}{I_{z}}}} . \)
Η σ m a x {\displaystyle \ \sigma _{max}} δεν μπορεί να ξεπερνά μια τιμή που είναι χαρακτηριστική για το υλικό. Στα ψαθυρά υλικά μιλάμε για τη θλιπτική ή εφελκυστική αντοχή του ενώ στα όλκιμα υλικά για το όριο διαρροής. Από αυτόν τον περιορισμό προκύπτει η μέγιστη ελαστική ροπή στο στοιχείο. Κατά το σχεδιασμό στοιχείων με επιτρεπόμενες τάσεις η χαρακτηριστική τάση του υλικού μειώνεται σε κάποιο ποσοστό που δίνεται από τον συντελεστή ασφαλείας. Στόχος είναι να καλυφθεί η αβεβαιότητα της πραγματικής αντοχής και να μειωθεί η πιθανότητα αστοχίας.
Ελαστοπλαστική ανάλυση
Ροπή μεγαλύτερη από την μέγιστη ελαστική προκαλεί θραύση στα ψαθυρά υλικά. Στα όλκιμα υλικά όμως το όριο διαρροής δεν ταυτίζεται με το όριο θραύσης. Όπως φαίνεται στο σχήμα 3 σε μεγαλύτερη φόρτιση τα πιο απομακρυσμένα τμήματα της διατομής εμφανίζουν πλαστικές παραμορφώσεις, ενώ το κέντρο της διατομής παραμένει στην ελαστική περιοχή. Το εύρος του ελαστικού πυρήνα μειώνεται συνεχώς με την αύξηση της φόρτισης έως την πλήρη πλαστικοποίηση όλης της διατομής. Στην ελαστοπλαστική ανάλυση κατά προσέγγιση θεωρείται ότι το υλικό υπακούει στο νόμο του Χούκ μέχρι το όριο διαρροής του αλλά για επιπλέον παραμόρφωση η τάση παραμένει σταθερή (Σχήμα 4 απλοποιημένη καμπύλη τάσεων - παραμορφώσεων). Μετά την πλήρη πλαστικοποίηση οι παραμορφώσεις γίνονται πολύ μεγάλες και σχηματίζεται πλαστική άρθρωση.
Ελαστική γραμμή

Σχήμα 5. Παραμόρφωση λόγω κάμψης. Η μέγιστη υποχώρηση ή αλλιώς το μέγιστο βέλος κάμψης εμφανίζεται στο ελεύθερο (δεξιό) άκρο.
Κατά την κάμψη το σχήμα του σώματος είναι διαφορετικό από το αρχικό λόγω της παραμόρφωσης. Σε κάθε σημείο του σώματος αντιστοιχεί και μια μετατόπιση από την αρχική του θέση που ονομάζεται βέλος κάμψης. Το σχήμα του παραμορφωμένου άξονα του σώματος ονομάζεται ελαστική γραμμή και η συνάρτηση που δίνει τα βέλη κάμψης, δηλαδή την κατακόρυφη μετατόπιση ενός σημείου του άξονα σε σχέση με την αρχική του θέση, ονομάζεται εξίσωση της ελαστικής γραμμής. Ο υπολογισμός της ελαστικής γραμμής έχει μεγάλη σημασία στις τεχνικές κατασκευές. Πρέπει να εξασφαλίζεται ότι τα βέλη κάμψης δε δημιουργούν πρόβλημα ασφάλειας, λειτουργικότητας ή αισθητικής.
Η συνάρτηση της κλίσης φ του παραμοφωμένου στοιχείου σε κάθε θέση x είναι:
\({\displaystyle {\phi }_{(x)}={\frac {1}{EI_{z}}}\int -M_{(x)}\,dx+c_{1}} \)
Η εξίσωση της ελαστικής γραμμής είναι:
\( {\displaystyle {w}_{(x)}={\frac {1}{EI_{z}}}\iint -M_{(x)}\,dx+c_{1}x+c_{2}} \)
ή
\({\displaystyle {w}_{(x)}=\int {\phi }_{(x)}\,dx+c_{2}} \)
όπου:
\( {\displaystyle \ E}\) : Το μέτρο ελαστικότητας του υλικού.
\( {\displaystyle \ I_{z}}\) : Η ροπή αδράνειας.
\( {\displaystyle \ M_{(x)}} \): Η ροπή κάμψης σε συνάρτηση με την απόσταση x.
\( {\displaystyle \ c_{1},c_{2}} \): Σταθερές ολοκλήρωσης που προκύπτουν από τις συνθήκες στήριξης. Θα πρέπει οι \( {\displaystyle \ w_{(x)}} \)και \( {\displaystyle \ {\phi }_{(x)}} \)να μηδενίζουν στις θέσεις που υπάρχει εμπόδιο κατακόρυφης μετατόπισης και στροφής αντίστοιχα.
Παράδειγμα υπολογισμού τάσεων και παραμοφώσεων

Σχήμα 6. Διάγραμμα τέμνουσας δύναμης Q {\displaystyle Q} και ροπής κάμψης M {\displaystyle M} σε πρόβολο δοκό.
Στο σχήμα 6 μια δοκός πρόβολος ορθογωνικής διατομής φορτίζεται στο ελεύθερο άκρο της από μια δύναμη P.
\( {\displaystyle I_{z}=\int _{A}z^{2}\,dA={\frac {bh^{3}}{12}}} \), με A το χωρίο που ορίζει η διατομή, b το πλάτος της διατομής, και h το υψος της.
\( {\displaystyle \ M_{(x)}=-Px} \) η συνάρτηση της ροπή κάμψης σε απόσταση x από το ελεύθερο άκρο.
Το διάγραμμα που δείχνει τη ροπή κάμψης Μ σε κάθε θέση παρουσιάζεται στο σχήμα 2 και έχει τη μέγιστη τιμή -PL στο πακτωμένο άκρο. Η μέγιστη ορθή τάση εμφανίζεται στις ίνες που έχουν τη μεγαλύτερη απόσταση από τον άξονα y. Λόγω της συμμετρίας της διατομής η απόσταση αυτή είναι h/2 για την άνω εφελκυόμενη και την κάτω θλιβόμενη ίνα και οι αντίστοιχες τάσεις έχουν την ίδια αριθμητική τιμή.
\( {\displaystyle \ \sigma _{max}={\frac {M_{max}z_{max}}{I_{z}}}=\pm {\frac {6PL}{bh^{2}}}} \)
Το σχήμα 5 δείχνει μια παρόμοια παραμορφωμένη κατάσταση όπου μπορούμε να διακρίνουμε πως οι πάνω ίνες της δοκού εφελκύονται ενώ οι κάτω θλίβονται.
Κλίση:
\( {\displaystyle {\phi }_{(x)}={\frac {1}{EI_{z}}}\int {Px}\,dx+c_{1}={\frac {Px^{2}}{2EI_{z}}}+c_{1}} \)
Στην πάκτωση:
\( {\displaystyle {\phi }_{(L)}=0=>c_{1}=-{\frac {PL^{2}}{2EI_{z}}}} \)
Άρα η συνάρτηση της κλίσης:
\( {\displaystyle {\phi }_{(x)}={\frac {Px^{2}}{2EI_{z}}}-{\frac {PL^{2}}{2EI_{z}}}} \)
Βέλος κάμψης:
\( {\displaystyle w_{(x)}={\frac {1}{EI_{z}}}\iint Px\,dx+c_{1}x+c_{2}={\frac {Px^{3}}{6EI_{z}}}-{\frac {PL^{2}}{2EI_{z}}}x+c_{2}} \)
Στην πάκτωση:\)
\({\displaystyle {w}_{(L)}=0=>c_{2}={\frac {PL^{3}}{3EI_{z}}}}
Άρα η εξίσωση της ελαστικής γραμμής:
\( {\displaystyle w_{(x)}={\frac {Px^{3}}{6EI_{z}}}-{\frac {PL^{2}}{2EI_{z}}}x+{\frac {PL^{3}}{3EI_{z}}}} \)
\( {\displaystyle w_{max}=w_{(0)}={\frac {PL^{3}}{3EI_{z}}}={\frac {4PL^{3}}{Ebh^{3}}}} \)
Σημειώσεις
Aκριβέστερα η εντατική κατάσταση που προκύπτει.
Στις λοξές δυνάμεις ή ροπές, την κάμψη προκαλούν οι κάθετες συνιστώσες. Οι παράλληλες συνιστώσες των δυνάμεων προκαλούν θλίψη ή εφελκυσμό ενώ των ροπών προκαλούν στρέψη.
Η καμπτική εντατική κατάσταση διαφέρει από τον λυγισμό. Αιτία του λυγισμού είναι δυνάμεις παράλληλες στον άξονα του σώματος ενώ της κάμψης οι κάθετες δυνάμεις και οι ροπές. Ο λυγισμός δεν είναι εντατική κατάσταση αλλά απώλεια της ευστάθειας του σώματος από δυνάμεις που το συνθλίβουν κατά τη διεύθυνση του κύριου άξονά του.
Διατομή ονομάζεται η επιφάνεια που είναι κάθετη στον κύριο άξονα. Παράδειγμα στο σχήμα 2 η διατομή είναι τετραγωνικού σχήματος.
Πηγές
Παναγιώτης Α. Βουθούνης Τεχνική μηχανική αντοχή των υλικών, Αθήνα, 1993
Γ.Ι. Τσαμασφύρος Μηχανική παραμορφώσιμων σωμάτων Τόμος Ι και ΙΙ, 1990 Εκδόσεις Συμμετρία
Hellenica World - Scientific Library
Από τη ελληνική Βικιπαίδεια http://el.wikipedia.org . Όλα τα κείμενα είναι διαθέσιμα υπό την GNU Free Documentation License

