In physics, Landau damping, named after its discoverer,[1]Soviet physicist Lev Davidovich Landau (1908–68), is the effect of damping (exponential decrease as a function of time) of longitudinal space charge waves in plasma or a similar environment.[2] This phenomenon prevents an instability from developing, and creates a region of stability in the parameter space. It was later argued by Donald Lynden-Bell that a similar phenomenon was occurring in galactic dynamics,[3] where the gas of electrons interacting by electrostatic forces is replaced by a "gas of stars" interacting by gravitational forces.[4] Landau damping can be manipulated exactly in numerical simulations such as particle-in-cell simulation.[5] It was proved to exist experimentally by Malmberg and Wharton in 1964,[6] almost two decades after its prediction by Landau in 1946.[7]
Wave–particle interactions
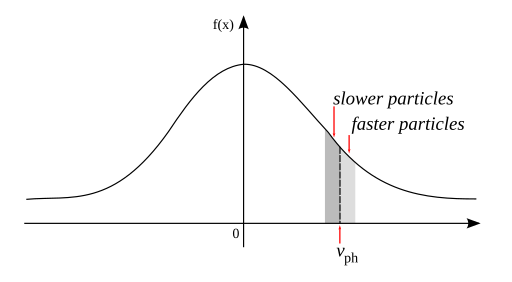
Landau damping occurs because of the energy exchange between an electromagnetic wave with phase velocity \( {\displaystyle v_{\text{ph}}} \) and particles in the plasma with velocity approximately equal to \( {\displaystyle v_{\text{ph}}} \), which can interact strongly with the wave.[8] Those particles having velocities slightly less than \( {\displaystyle v_{\text{ph}}} \) will be accelerated by the electric field of the wave to move with the wave phase velocity, while those particles with velocities slightly greater than \( {\displaystyle v_{\text{ph}}} \) will be decelerated losing energy to the wave: particles tend to synchronize with the wave. This is proved experimentally with a Traveling-wave tube.[9]
In an ideal MHD plasma the particle velocities are often taken to be approximately a Maxwellian distribution function. If the slope of the function is negative, the number of particles with velocities slightly less than the wave phase velocity is greater than the number of particles with velocities slightly greater. Hence, there are more particles gaining energy from the wave than losing to the wave, which leads to wave damping. If, however, the slope of the function is positive, the number of particles with velocities slightly less than the wave phase velocity is smaller than the number of particles with velocities slightly greater. Hence, there are more particles losing energy to the wave than gaining from the wave, which leads to a resultant increase in the wave energy.
Physical interpretation
The mathematical theory of Landau damping is somewhat involved—see the section below. However, there is a simple physical interpretation [introduced in section 7.5 of [2] with a caveat], which, though not strictly correct, helps to visualize this phenomenon.
It is possible to imagine Langmuir waves as waves in the sea, and the particles as surfers trying to catch the wave, all moving in the same direction. If the surfer is moving on the water surface at a velocity slightly less than the waves he will eventually be caught and pushed along the wave (gaining energy), while a surfer moving slightly faster than a wave will be pushing on the wave as he moves uphill (losing energy to the wave).
It is worth noting that only the surfers are playing an important role in this energy interactions with the waves; a beachball floating on the water (zero velocity) will go up and down as the wave goes by, not gaining energy at all. Also, a boat that moves very fast (faster than the waves) does not exchange much energy with the wave.
A simple mechanical description of particle dynamics provides a quantitative estimate of the synchronization of particles with the wave [Equation (1) of [9]]. A more rigorous approach shows the strongest synchronization occurs for particles with a velocity in the wave frame proportional to the damping rate and independent of the wave amplitude [section 4.1.3 of [10]]. Since Landau damping occurs for waves with arbitrarily small amplitudes, this shows the most active particles in this damping are far from being trapped. This is natural, since trapping involves diverging time scales for such waves (specifically \( {\displaystyle T_{\text{trap}}\sim A^{-1/2}} \) for a wave amplitude A).
Theoretical physics: perturbation theory in a Vlasovian frame
Theoretical treatment starts with the Vlasov equation in the non-relativistic zero-magnetic field limit, the Vlasov–Poisson set of equations. Explicit solutions are obtained in the limit of a small E-field. The distribution function f and field E are expanded in a series: \( f=f_{0}(v)+f_{1}(x,v,t)+f_{2}(x,v,t) \), \( E=E_{1}(x,t)+E_{2}(x,t) \) and terms of equal order are collected.
To first order the Vlasov–Poisson equations read
\( {\displaystyle (\partial _{t}+v\partial _{x})f_{1}+{e \over m}E_{1}f'_{0}=0,\quad \partial _{x}E_{1}={e \over \epsilon _{0}}\int f_{1}\mathrm {d} v}. \)
Landau calculated[1] the wave caused by an initial disturbance \( f_{1}(x,v,0)=g(v)\exp(ikx) \) and found by aid of Laplace transform and contour integration a damped travelling wave of the form \( {\displaystyle \exp[ik(x-v_{\text{ph}}t)-\gamma t]} \)with wave number k and damping decrement
\( {\displaystyle \gamma \approx -{\pi \omega _{p}^{3} \over 2k^{2}N}f'_{0}(v_{\text{ph}}),\quad N=\int f_{0}\mathrm {d} v}. \)
Here ω p {\displaystyle \omega _{p}} \omega _{p} is the plasma oscillation frequency and N is the electron density. Later Nico van Kampen proved[11] that the same result can be obtained with Fourier transform. He showed that the linearized Vlasov–Poisson equations have a continuous spectrum of singular normal modes, now known as van Kampen modes
\( {\displaystyle {\frac {\omega _{p}^{2}}{kN}}f'_{0}{\frac {\mathcal {P}}{kv-\omega }}+\epsilon \delta \left(v-{\frac {\omega }{k}}\right)} \)
in which P {\displaystyle {\mathcal {P}}} {\mathcal {P}} signifies principal value, δ {\displaystyle \delta } \delta is the delta function (see generalized function) and
\( {\displaystyle \epsilon =1+{\frac {\omega _{p}^{2}}{kN}}\int f'_{0}{\frac {\mathcal {P}}{\omega -kv}}\mathrm {d} v} \)
is the plasma permittivity. Decomposing the initial disturbance in these modes he obtained the Fourier spectrum of the resulting wave. Damping is explained by phase-mixing of these Fourier modes with slightly different frequencies near \( \omega _{p} \) .
It was not clear how damping could occur in a collisionless plasma: where does the wave energy go? In fluid theory, in which the plasma is modeled as a dispersive dielectric medium,[12] the energy of Langmuir waves is known: field energy multiplied by the Brillouin factor \( \partial _{\omega }(\omega \epsilon ) \) . But damping cannot be derived in this model. To calculate energy exchange of the wave with resonant electrons, Vlasov plasma theory has to be expanded to second order and problems about suitable initial conditions and secular terms arise.
Ldamp2.jpg
In Ref.[13] these problems are studied. Because calculations for an infinite wave are deficient in second order, a wave packet is analysed. Second-order initial conditions are found that suppress secular behavior and excite a wave packet of which the energy agrees with fluid theory. The figure shows the energy density of a wave packet traveling at the group velocity, its energy being carried away by electrons moving at the phase velocity. Total energy, the area under the curves, is conserved.
Mathematical theory: the Cauchy problem for perturbative solutions
The rigorous mathematical theory is based on solving the Cauchy problem for the evolution equation (here the partial differential Vlasov–Poisson equation) and proving estimates on the solution.
First a rather complete linearized mathematical theory has been developed since Landau.[14]
Going beyond the linearized equation and dealing with the nonlinearity has been a longstanding problem in the mathematical theory of Landau damping. Previously one mathematical result at the non-linear level was the existence of a class of exponentially damped solutions of the Vlasov–Poisson equation in a circle which had been proved in[15] by means of a scattering technique (this result has been recently extended in[16]). However these existence results do not say anything about which initial data could lead to such damped solutions.
In a recent paper[17] the initial data issue is solved and Landau damping is mathematically established for the first time for the non-linear Vlasov equation. It is proved that solutions starting in some neighborhood (for the analytic or Gevrey topology) of a linearly stable homogeneous stationary solution are (orbitally) stable for all times and are damped globally in time. The damping phenomenon is reinterpreted in terms of transfer of regularity of f as a function of x and v, respectively, rather than exchanges of energy. Large scale variations pass into variations of smaller and smaller scale in velocity space, corresponding to a shift of the Fourier spectrum of f as a function of v. This shift, well known in linear theory, proves to hold in the non-linear case.
Theoretical physics: perturbation theory in an N-body frame [18]
An expression of plasma permittivity analogous to the above one, but corresponding to the Laplace transform used by Landau, can be obtained simply in an N-body frame. One considers a (one-component) plasma where only electrons are present as particles, and ions just provide a uniform neutralizing background. The principle of the calculation is provided by considering the fictitious linearized motion of a single particle in a single Fourier component of its own electric field. The full calculation boils down to a summation of the corresponding result over all N {\displaystyle N} N particles and all Fourier components. The Vlasovian expression for the plasma permittivity is finally recovered by substituting an integral over a smooth distribution function for the discrete sum over the particles in the N-body plasma permittivity. Together with Landau damping, this mechanical approach also provides the calculation of Debye shielding, or Electric-field screening, in a plasma.
See also
List of plasma (physics) articles
Notes and references
Landau, L. "On the vibration of the electronic plasma". JETP 16 (1946), 574. English translation in J. Phys. (USSR) 10 (1946), 25. Reproduced in Collected papers of L.D. Landau, edited and with an introduction by D. ter Haar, Pergamon Press, 1965, pp. 445–460; and in Men of Physics: L.D. Landau, Vol. 2, Pergamon Press, D. ter Haar, ed. (1965).
Chen, Francis F. Introduction to Plasma Physics and Controlled Fusion. Second Ed., 1984 Plenum Press, New York.
Lynden-Bell, D (1962). "The stability and vibrations of a gas of stars". Mon. Not. R. Astron. Soc. 124 (4): 279–296. Bibcode:1962MNRAS.124..279L. doi:10.1093/mnras/124.4.279.
Binney, J., and Tremaine, S. Galactic Dynamics, second ed. Princeton Series in Astrophysics. Princeton University Press, 2008.
Woo Myung, Chang; Koo Lee, Jae (2014). "Finite Amplitude Effects on Landau Damping and Diminished Transportation of Trapped Electrons". Journal of the Physical Society of Japan. 83 (7): 074502. Bibcode:2014JPSJ...83g4502M. doi:10.7566/jpsj.83.074502.
Malmberg, J. H.; Wharton, C. B. (1964-08-10). "Collisionless Damping of Electrostatic Plasma Waves". Physical Review Letters. 13 (6): 184–186. Bibcode:1964PhRvL..13..184M. doi:10.1103/PhysRevLett.13.184.
Landau, L. D. "On the vibrations of the electronic plasma". Zh. Eksp. Teor. Fiz. 16: 574–86 (reprinted 1965 Collected Papers of Landau ed D ter Haar (Oxford: Pergamon) pp 445–60).
Tsurutani, B.; Lakhina, G. (1997). "Some basic concepts of wave–particle interactions in collisionless plasmas". Reviews of Geophysics. 35 (4): 491–502. Bibcode:1997RvGeo..35..491T. doi:10.1029/97rg02200.
Doveil, F.; Escande, D. F.; Macor, A. (2005-03-04). "Experimental Observation of Nonlinear Synchronization due to a Single Wave". Physical Review Letters. 94 (8): 085003. Bibcode:2005PhRvL..94h5003D. doi:10.1103/PhysRevLett.94.085003. PMID 15783900.
Escande, Dominique; Elskens, Yves (2002-10-23). Microscopic Dynamics of Plasmas and Chaos. Microscopic Dynamics of Plasmas and Chaos. Series: Series in Plasma Physics. Series in Plasma Physics. 12. Bibcode:2002SPP....12.....E. doi:10.1201/9781420033953. ISBN 9780750306126.
van Kampen, N. G., "On the theory of stationary waves in plasma", Physica 21 (1955), 949–963. See http://theor.jinr.ru/~kuzemsky/kampenbio.html
Landau, L. D. and Lifshitz, E. M., Electrodynamics of Continuous Media §80, Pergamon Press (1984).
Best, Robert W. B., "Energy and momentum density of a Landau-damped wave packet", J. Plasma Phys. 63 (2000), 371-391
See for instance Backus, G. "Linearized plasma oscillations in arbitrary electron distributions". J. Math. Phys. 1 (1960), 178–191, 559. Degond, P. "Spectral theory of the linearized Vlasov–Poisson equation". Trans. Amer. Math. Soc. 294, 2 (1986), 435–453. Maslov, V. P., and Fedoryuk, M. V. "The linear theory of Landau damping." Mat. Sb. (N.S.) 127(169), 4 (1985), 445–475, 559.
Caglioti, E.; Maffei, C. (1998). "Time asymptotics for solutions of Vlasov–Poisson equation in a circle". J. Statist. Phys. 92: 1–2, 301–323. doi:10.1023/A:1023092317419.
Hwang, H. J. and Velasquez J. J. L. "On the Existence of Exponentially Decreasing Solutions of the Nonlinear Landau Damping Problem", Indiana Univ. Math. J. 68, 6 (2009), 2623–2660
Mouhot, C., and Villani, C. "On Landau damping", Acta Math. 207, 1 (2011), 29–201 (quoted for the Fields Medal awarded to Cédric Villani in 2010)
Escande, D F; Doveil, F; Elskens, Yves (2016). "N -body description of Debye shielding and Landau damping". Plasma Physics and Controlled Fusion. 58 (1): 014040. arXiv:1506.06468. Bibcode:2016PPCF...58a4040E. doi:10.1088/0741-3335/58/1/014040.
Hellenica World - Scientific Library
Retrieved from "http://en.wikipedia.org/"
All text is available under the terms of the GNU Free Documentation License