In fluid dynamics, the process of a laminar flow becoming turbulent is known as laminar–turbulent transition. The main parameter characterizing transition is the Reynolds number.
Transition is often described as a process proceeding through a series of stages. "Transitional flow" can refer to transition in either direction, that is laminar–turbulent transitional or turbulent–laminar transitional flow.
The process applies to any fluid flow, and is most often used in the context of boundary layers.
History
Reynolds’ 1883 experiment on fluid dynamics in pipes
Reynolds’ 1883 observations of the nature of the flow in his experiments
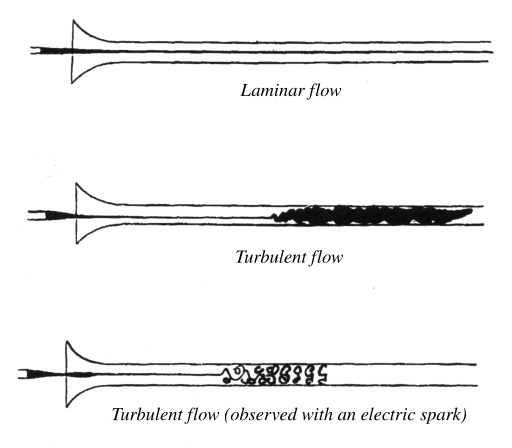
In 1883 Osborne Reynolds demonstrated the transition to turbulent flow in a classic experiment in which he examined the behaviour of water flow under different flow rates using a small jet of dyed water introduced into the centre of flow in a larger pipe.
The larger pipe was glass, so the behaviour of the layer of dyed flow could be observed, and at the end of this pipe was a flow-control valve used to vary the water velocity inside the tube. When the velocity was low, the dyed layer remained distinct through the entire length of the large tube. When the velocity was increased, the layer broke up at a given point and diffused throughout the fluid's cross-section. The point at which this happened was the transition point from laminar to turbulent flow. Reynolds identified the governing parameter for the onset of this effect, which was a dimensionless constant later called the Reynolds number.
Reynolds found that the transition occurred between Re = 2000 and 13000, depending on the smoothness of the entry conditions. When extreme care is taken, the transition can even happen with Re as high as 40000. On the other hand, Re = 2000 appears to be about the lowest value obtained at a rough entrance.[1]
Reynolds' publications in fluid dynamics began in the early 1870s. His final theoretical model published in the mid-1890s is still the standard mathematical framework used today. Examples of titles from his more groundbreaking reports are:
Improvements in Apparatus for Obtaining Motive Power from Fluids and also for Raising or Forcing Fluids (1875)
An experimental investigation of the circumstances which determine whether the motion of water in parallel channels shall be direct or sinuous and of the law of resistance in parallel channels (1883)
On the dynamical theory of incompressible viscous fluids and the determination of the criterion (1895)
Transition stages in a boundary layer
Morkovin's path to transition
The path from receptivity to laminar-turbulent transition as illustrated by Morkovin, 1994.[2]
A boundary layer can transition to turbulence through a number of paths. Which path is realized physically depends on the initial conditions such as initial disturbance amplitude and surface roughness. The level of understanding of each phase varies greatly, from near complete understanding of primary mode growth to a near-complete lack of understanding of bypass mechanisms.
Receptivity
The initial stage of the natural transition process is known as the Receptivity phase and consists of the transformation of environmental disturbances – both acoustic (sound) and vortical (turbulence) – into small perturbations within the boundary layer. The mechanisms by which these disturbances arise are varied and include freestream sound and/or turbulence interacting with surface curvature, shape discontinuities and surface roughness. These initial conditions are small, often unmeasurable perturbations to the basic state flow. From here, the growth (or decay) of these disturbances depends on the nature of the disturbance and the nature of the basic state. Acoustic disturbances tend to excite two-dimensional instabilities such as Tollmien–Schlichting waves (T-S waves), while vortical disturbances tend to lead to the growth of three-dimensional phenomena such as the crossflow instability.[3]
Numerous experiments in recent decades have revealed that the extent of the amplification region, and hence the location of the transition point on the body surface, is strongly dependent not only upon the amplitude and/or the spectrum of external disturbances but also on their physical nature. Some of the disturbances easily penetrate into the boundary layer whilst others do not. Consequently, the concept of boundary layer transition is a complex one and still lacks a complete theoretical exposition.
Primary mode growth
If the initial, environmentally-generated disturbance is small enough, the next stage of the transition process is that of primary mode growth. In this stage, the initial disturbances grow (or decay) in a manner described by linear stability theory.[4] The specific instabilities that are exhibited in reality depend on the geometry of the problem and the nature and amplitude of initial disturbances. Across a range of Reynolds numbers in a given flow configuration, the most amplified modes can and often do vary.
There are several major types of instability which commonly occur in boundary layers. In subsonic and early supersonic flows, the dominant two-dimensional instabilities are T-S waves. For flows in which a three-dimensional boundary layer develops such as a swept wing, the crossflow instability becomes important. For flows navigating concave surface curvature, Görtler vortices may become the dominant instability. Each instability has its own physical origins and its own set of control strategies - some of which are contraindicated by other instabilities – adding to the difficulty in controlling laminar-turbulent transition.
Simple harmonic boundary layer sound in the physics of transition to turbulence
Simple harmonic sound as a precipitating factor in the sudden transition from laminar to turbulent flow might be attributed to Elizabeth Barrett Browning. Her poem, Aurora Leigh (1856), revealed how musical notes (the pealing of a particular church bell), triggered wavering turbulence in the previously steady laminar-flow flames of street gaslights (“...gaslights tremble in the streets and squares”: Hair 2016). Her instantly acclaimed poem might have alerted scientists (e.g., Leconte 1859) to the influence of simple harmonic (SH) sound as a cause of turbulence. A contemporary flurry of scientific interest in this effect culminated in Sir John Tyndall (1867) deducing that specific SH sounds, directed perpendicular to the flow had waves that blended with similar SH waves created by friction along the boundaries of tubes, amplifying them and triggering the phenomenon of high-resistance turbulent flow. His interpretation re-surfaced over 100 years later (Hamilton 2015).
Tollmien (1931) and Schlichting (1929) proposed that friction (viscosity) along a smooth flat boundary, created SH boundary layer (BL) oscillations that gradually increased in amplitude until turbulence erupted. Although contemporary wind tunnels failed to confirm the theory, Schubauer and Skramstad (1943) created a refined wind tunnel that deadened the vibrations and sounds that might impinge on the wind tunnel flat plate flow studies. They confirmed the development of SH long-crested BL oscillations, the dynamic shear waves of transition to turbulence. They showed that specific SH fluttering vibrations induced electromagnetically into a BL ferromagnetic ribbon could amplify similar flow-induced SH BL flutter (BLF) waves, precipitating turbulence at much lower flow rates. Furthermore, certain other specific frequencies interfered with the development of the SH BLF waves, preserving laminar flow to higher flow rates.
An oscillation of a mass in a fluid is a vibration that creates a sound wave. SH BLF oscillations in boundary layer fluid along a flat plate must produce SH sound that reflects off the boundary perpendicular to the fluid laminae. In late transition, Schubauer and Skramstad found foci of amplification of BL oscillations, associated with bursts of noise (“turbulent spots”). Focal amplification of the transverse sound in late transition was associated with BL vortex formation.
The focal amplified sound of turbulent spots along a flat plate with high energy oscillation of molecules perpendicularly through the laminae, might suddenly cause localized freezing of laminar slip. The sudden braking of “frozen” spots of fluid would transfer resistance to the high resistance at the boundary, and might explain the head-over-heels BL vortices of late transition. Osborne Reynolds described similar turbulent spots during transition in water flow in cylinders (“flashes of turbulence,” 1883).
When many random vortices erupt as turbulence onsets, the generalized freezing of laminar slip (laminar interlocking) is associated with noise and a dramatic increase in resistance to flow. This might also explain the parabolic isovelocity profile of laminar flow abruptly changing to the flattened profile of turbulent flow – as laminar slip is replaced by laminar interlocking as turbulence erupts (Hamilton 2015).
[5]
Secondary instabilities
The primary modes themselves don't actually lead directly to breakdown, but instead lead to the formation of secondary instability mechanisms. As the primary modes grow and distort the mean flow, they begin to exhibit nonlinearities and linear theory no longer applies. Complicating the matter is the growing distortion of the mean flow, which can lead to inflection points in the velocity profile a situation shown by Lord Rayleigh to indicate absolute instability in a boundary layer. These secondary instabilities lead rapidly to breakdown. These secondary instabilities are often much higher in frequency than their linear precursors.
See also
Transition modeling
References
Fung, Y. C. (1990). Biomechanics – Motion, flow, stress and growth. New York (USA): Springer-Verlag. p. 569.
Morkovin M. V., Reshotko E., Herbert T. 1994. "Transition in open flow systems—a reassessment". Bull. Am. Phys. Soc. 39:1882.
Saric W. S., Reed H. L., Kerschen E. J. 2002. "Boundary-layer receptivity to freestream disturbances". Annu. Rev. Fluid Mech. 34:291–319.
Mack L. M. 1984. "Boundary-layer linear stability theory". AGARD Rep. No. 709.
E. B. BROWNING, Aurora Leigh, Chapman and Hall, Book 8, lines 44–48 (1857). D. S. HAIR, Fresh Strange Music – Elizabeth Barrett Browning’s Language, McGill-Queens University Press, London, Ontario, 214–217 (2015). G. HAMILTON, Simple Harmonics, Aylmer Express, Aylmer, Ontario (2015). J. LECONTE, Phil. Mag., 15, 235-239 (1859 Klasse, 181–208 (1933). REYNOLDS Phil. Trans. Roy. Soc., London 174, 935–998 (1883). W. TOLLMIEN, Über die Enstehung der Turbulenz. 1. Mitteilung, Nachichten der Gesellschaft der Wissenshaften (1931). H. SCHLICHTING, Zur Enstehung der Turbulenz bei der Plattenströmung. Nachrichten der Gesellschaft der Wissenschaften – enshaften zu Göttingen, Mathematisch – Physikalische zu Göttingen, Mathematisch – Physikalische Klasse, 21–44 (1929).
Hellenica World - Scientific Library
Retrieved from "http://en.wikipedia.org/"
All text is available under the terms of the GNU Free Documentation License