The empty lattice approximation is a theoretical electronic band structure model in which the potential is periodic and weak (close to constant). One may also consider an empty irregular lattice, in which the potential is not even periodic.[1] The empty lattice approximation describes a number of properties of energy dispersion relations of non-interacting free electrons that move through a crystal lattice. The energy of the electrons in the "empty lattice" is the same as the energy of free electrons. The model is useful because it clearly illustrates a number of the sometimes very complex features of energy dispersion relations in solids which are fundamental to all electronic band structures.
Scattering and periodicity
Free electron bands in a one dimensional lattice
The periodic potential of the lattice in this free electron model must be weak because otherwise the electrons wouldn't be free. The strength of the scattering mainly depends on the geometry and topology of the system. Topologically defined parameters, like scattering cross sections, depend on the magnitude of the potential and the size of the potential well. For 1-, 2- and 3-dimensional spaces potential wells do always scatter waves, no matter how small their potentials are, what their signs are or how limited their sizes are. For a particle in a one-dimensional lattice, like the Kronig–Penney model, it is possible to calculate the band structure analytically by substituting the values for the potential, the lattice spacing and the size of potential well.[2] For two and three-dimensional problems it is more difficult to calculate a band structure based on a similar model with a few parameters accurately. Nevertheless, the properties of the band structure can easily be approximated in most regions by perturbation methods.
In theory the lattice is infinitely large, so a weak periodic scattering potential will eventually be strong enough to reflect the wave. The scattering process results in the well known Bragg reflections of electrons by the periodic potential of the crystal structure. This is the origin of the periodicity of the dispersion relation and the division of k-space in Brillouin zones. The periodic energy dispersion relation is expressed as:
\( {\displaystyle E_{n}(\mathbf {k} )={\frac {\hbar ^{2}(\mathbf {k} +\mathbf {G} _{n})^{2}}{2m}}} \)
The \( {\displaystyle \mathbf {G} _{n}} \) are the reciprocal lattice vectors to which the bands \( {\displaystyle E_{n}(\mathbf {k} )} \) belong.
The figure on the right shows the dispersion relation for three periods in reciprocal space of a one-dimensional lattice with lattice cells of length a.
The energy bands and the density of states
In a one-dimensional lattice the number of reciprocal lattice vectors \( {\displaystyle \mathbf {G} _{n}} \) that determine the bands in an energy interval is limited to two when the energy rises. In two and three dimensional lattices the number of reciprocal lattice vectors that determine the free electron bands \( {\displaystyle E_{n}(\mathbf {k} )} \) increases more rapidly when the length of the wave vector increases and the energy rises. This is because the number of reciprocal lattice vectors \( {\displaystyle \mathbf {G} _{n}} \) that lie in an interval \( {\displaystyle [\mathbf {k} ,\mathbf {k} +d\mathbf {k} ]} \) increases. The density of states in an energy interval [E,E+dE] depends on the number of states in an interval \( {\displaystyle [\mathbf {k} ,\mathbf {k} +d\mathbf {k} ]} \) in reciprocal space and the slope of the dispersion relation \( {\displaystyle E_{n}(\mathbf {k} )} \) .
Figure 3: Free-electron DOS in 3-dimensional k-space
Though the lattice cells are not spherically symmetric, the dispersion relation still has spherical symmetry from the point of view of a fixed central point in a reciprocal lattice cell if the dispersion relation is extended outside the central Brillouin zone. The density of states in a three-dimensional lattice will be the same as in the case of the absence of a lattice. For the three-dimensional case the density of states \( D_{3}\left(E\right) \) is;
\( D_{3}\left(E\right)=2\pi {\sqrt {\frac {E-E_{0}}{c_{k}^{3}}}}\ . \)
In three-dimensional space the Brillouin zone boundaries are planes. The dispersion relations show conics of the free-electron energy dispersion parabolas for all possible reciprocal lattice vectors. This results in a very complicated set intersecting of curves when the dispersion relations are calculated because there is a large number of possible angles between evaluation trajectories, first and higher order Brillouin zone boundaries and dispersion parabola intersection cones.
Second, third and higher Brillouin zones
FCC Brillouin zone
"Free electrons" that move through the lattice of a solid with wave vectors \( \mathbf {k} \) far outside the first Brillouin zone are still reflected back into the first Brillouin zone. See the external links section for sites with examples and figures.
The nearly free electron model
Main article: Nearly free electron model
In most simple metals, like aluminium, the screening effect strongly reduces the electric field of the ions in the solid. The electrostatic potential is expressed as
\( V(r)={\frac {Ze}{r}}e^{{-qr}} \)
where Z is the atomic number, e is the elementary unit charge, r is the distance to the nucleus of the embedded ion and q is a screening parameter that determines the range of the potential. The Fourier transform, \( {\displaystyle U_{\mathbf {G} }} \), of the lattice potential, \( V({\mathbf {r}}) \), is expressed as
\( {\displaystyle U_{\mathbf {G} }={\frac {4\pi Ze}{q^{2}+G^{2}}}} \)
When the values of the off-diagonal elements \( {\displaystyle U_{\mathbf {G} }} \) between the reciprocal lattice vectors in the Hamiltonian almost go to zero. As a result, the magnitude of the band gap \( {\displaystyle 2|U_{\mathbf {G} }|} \) collapses and the empty lattice approximation is obtained.
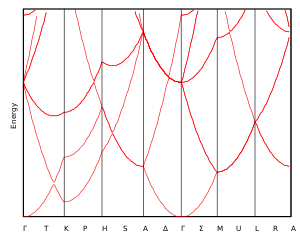
The electron bands of common metal crystals
Apart from a few exotic exceptions, metals crystallize in three kinds of crystal structures: the BCC and FCC cubic crystal structures and the hexagonal close-packed HCP crystal structure.

-
Body-centered cubic (I)
-

Face-centered cubic (F)
-
Hexagonal close-packed


References
Physics Lecture Notes. P.Dirac, Feynman,R.,1968. Internet, Amazon,25.03.2014.
C. Kittel (1953–1976). Introduction to Solid State Physics. Wiley & Sons. ISBN 978-0-471-49024-1.
External links
Brillouin Zone simple lattice diagrams by Thayer Watkins
Brillouin Zone 3d lattice diagrams by Technion.
DoITPoMS Teaching and Learning Package- "Brillouin Zones"
Hellenica World - Scientific Library
Retrieved from "http://en.wikipedia.org/"
All text is available under the terms of the GNU Free Documentation License




