Areal velocity

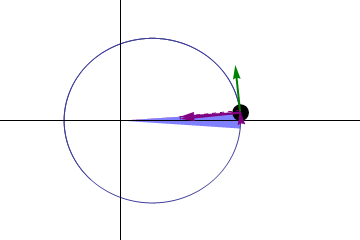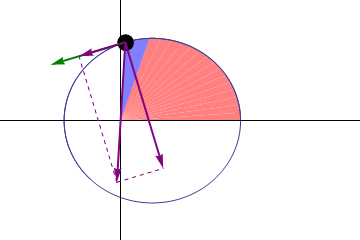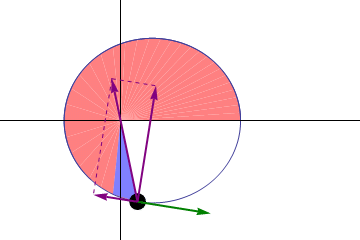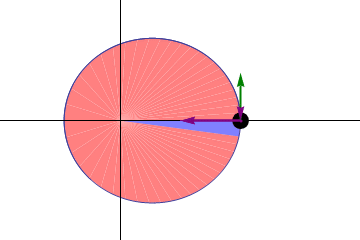
In classical mechanics, areal velocity (also called sector velocity or sectorial velocity) is the rate at which area is swept out by a particle as it moves along a curve. In the adjoining figure, suppose that a particle moves along the blue curve. At a certain time t, the particle is located at point B, and a short while later, at time t + Δt, the particle has moved to point C. The area swept out by the particle is the green area in the figure, bounded by the line segments AB and AC and the curve along which the particle moves. The areal velocity equals this area divided by the time interval Δt in the limit that Δt becomes vanishingly small. It is an example of a pseudovector (also called axial vector), pointing normal to the plane containing the position and velocity vectors of the particle.

Areal velocity is the area swept out per unit time by a particle moving along a curve da/dt=const (shown in blue).

Illustration of Kepler's second law. The planet moves faster near the Sun, so the same area is swept out in a given time as at larger distances, where the planet moves more slowly.

The concept of areal velocity is closely linked historically with the concept of angular momentum. Kepler's second law states that the areal velocity of a planet, with the sun taken as origin, is constant. Isaac Newton was the first scientist to recognize the dynamical significance of Kepler's second law. With the aid of his laws of motion, he proved in 1684 that any planet that is attracted to a fixed center sweeps out equal areas in equal intervals of time. By the middle of the 18th century, the principle of angular momentum was discovered gradually by Daniel Bernoulli and Leonhard Euler and Patrick d'Arcy; d'Arcy's version of the principle was phrased in terms of swept area. For this reason, the principle of angular momentum was often referred to in the older literature in mechanics as "the principle of equal areas." Since the concept of angular momentum includes more than just geometry, the designation "principle of equal areas" has been dropped in modern works.

Connection with angular momentum

In the situation of the first figure, the area swept out during time period Δt by the particle is approximately equal to the area of triangle ABC. As Δt approaches zero this near-equality becomes exact as a limit.

Let the point D be the fourth corner of parallelogram ABDC shown in the figure, so that the vectors AB and AC add up by the parallelogram rule to vector AD. Then the area of triangle ABC is half the area of parallelogram ABDC, and the area of ABDC is equal to the magnitude of the cross product of vectors AB and AC. This area can also be viewed as a vector with this magnitude, pointing in a direction perpendicular to the parallelogram; this vector is the cross product itself:

\( {\text{vector area of parallelogram }}ABCD={\vec {r}}(t)\times {\vec {r}}(t+\Delta t). \)

Hence

\( {\text{vector area of triangle }}ABC={\frac {{\vec {r}}(t)\times {\vec {r}}(t+\Delta t)}{2}}. \)

The areal velocity is this vector area divided by Δt in the limit that Δt becomes vanishingly small:

\( {\begin{aligned}{\text{areal velocity}}&=\lim _{{\Delta t\rightarrow 0}}{\frac {{\vec {r}}(t)\times {\vec {r}}(t+\Delta t)}{2\Delta t}}\\&=\lim _{{\Delta t\rightarrow 0}}{\frac {{\vec {r}}(t)\times {\bigl (}{\vec {r}}(t)+{\vec {r}}\,'(t)\Delta t{\bigr )}}{2\Delta t}}\\&=\lim _{{\Delta t\rightarrow 0}}{\frac {{\vec {r}}(t)\times {\vec {r}}\,'(t)}{2}}\left({\Delta t \over \Delta t}\right)\\&={\frac {{\vec {r}}(t)\times {\vec {r}}\,'(t)}{2}}.\end{aligned}} \)

But, \( {\vec {r}}\,'(t) \) is the velocity vector \( {\vec {v}}(t) \) of the moving particle, so that

\( {\frac {d{\vec {A}}}{dt}}={\frac {{\vec {r}}\times {\vec {v}}}{2}}. \)

On the other hand, the angular momentum of the particle is

\( {\vec {L}}={\vec {r}}\times m{\vec {v}}, \)

and hence the angular momentum equals 2m times the areal velocity.

Conservation of areal velocity is a general property of central force motion,[1] and, within the context of classical mechanics, is equivalent to the conservation of angular momentum.
References

"Chapter 6. Central Force Motion" (PDF).

Moulton, F. R. (1970) [1914]. An Introduction to Celestial Mechanics. Dover. ISBN 978-0-486-64687-9.
Goldstein, H. (1980). Classical Mechanics (2nd ed.). Addison-Wesley. ISBN 978-0-486-68063-7.
Casey, J. (2007). "Areal Velocity and Angular Momentum for Non-Planar Problems in Particle Mechanics". American Journal of Physics. 75 (8): 677–685. Bibcode:2007AmJPh..75..677C. doi:10.1119/1.2735630.
Brackenridge, J. B. (1995). The Key to Newton's Dynamics: The Kepler Problem and the Principia. Berkeley: University of California Press. doi:10.1525/j.ctt1ppn2m. ISBN 978-0-520-20217-7.