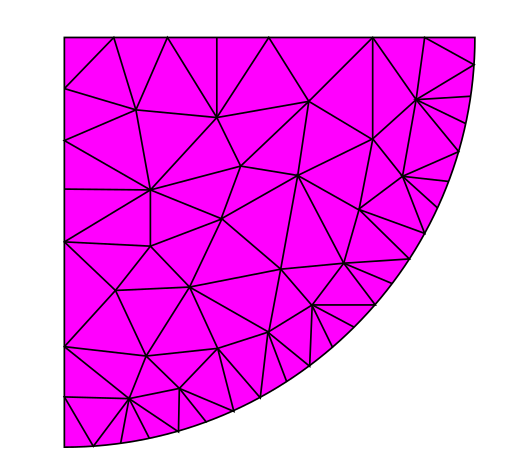
An unstructured (or irregular) grid is a tessellation of a part of the Euclidean plane or Euclidean space by simple shapes, such as triangles or tetrahedra, in an irregular pattern. Grids of this type may be used in finite element analysis when the input to be analyzed has an irregular shape.
Unlike structured grids, unstructured grids require a list of the connectivity which specifies the way a given set of vertices make up individual elements (see graph (data structure)).
Ruppert's algorithm is often used to convert an irregularly shaped polygon into an unstructured grid of triangles.
In addition to triangles and tetrahedra, other commonly used elements in finite element simulation include quadrilateral (4-noded) and hexahedral (8-noded) elements in 2D and 3D, respectively. One of the most commonly used algorithms to generate unstructured quadrilateral grid is "Paving".[citation needed] However, there is no such commonly used algorithm for generating unstructured hexahedral grid on a general 3D solid model. "Plastering" is a 3D version of Paving,[citation needed] but it has difficulty in forming hexahedral elements at the interior of a solid.
See also
Types of mesh
Regular grid
Mesh generation
Finite element analysis
Undergraduate Texts in Mathematics
Graduate Studies in Mathematics
Hellenica World - Scientific Library
Retrieved from "http://en.wikipedia.org/"
All text is available under the terms of the GNU Free Documentation License