In mathematics, particularly in differential geometry, an osculating plane is a plane in a Euclidean space or affine space which meets a submanifold at a point in such a way as to have a second order of contact at the point. The word osculate is from the Latin osculatus which is a past participle of osculari, meaning to kiss. An osculating plane is thus a plane which "kisses" a submanifold.
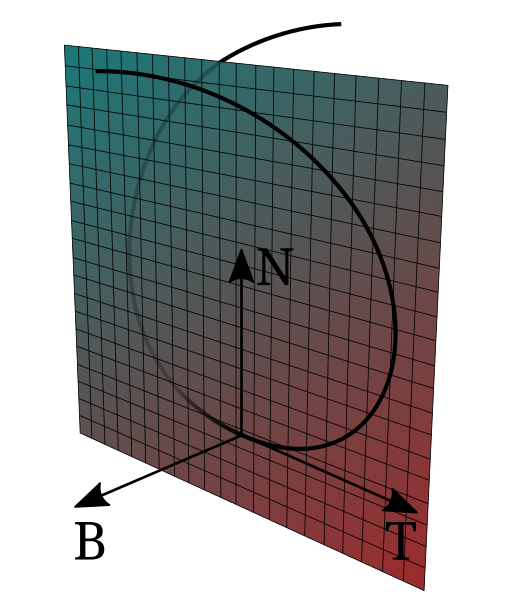
A space curve, Frenet–Serret frame, and the osculating plane (spanned by T and N).
The osculating plane in the geometry of Euclidean space curves can be described in terms of the Frenet-Serret formulas as the linear span of the tangent and normal vectors.
See also
Osculating circle
Differential geometry of curves#Special Frenet vectors and generalized curvatures
Undergraduate Texts in Mathematics
Graduate Studies in Mathematics
Hellenica World - Scientific Library
Retrieved from "http://en.wikipedia.org/"
All text is available under the terms of the GNU Free Documentation License