Napoleon's problem

Napoleon's problem is a compass construction problem. In it, a circle and its center are given. The challenge is to divide the circle into four equal arcs using only a compass.[1][2] Napoleon was known to be an amateur mathematician, but it is not known if he either created or solved the problem. Napoleon's friend the Italian mathematician Lorenzo Mascheroni introduced the limitation of using only a compass (no straight edge) into geometric constructions. But actually, the challenge above is easier than the real Napoleon's problem, consisting in finding the center of a given circle with compass alone. The following sections will describe solutions to three problems and proofs that they work.

Georg Mohr's 1672 book "Euclides Danicus" anticipated Mascheroni's idea, though the book was only rediscovered in 1928.

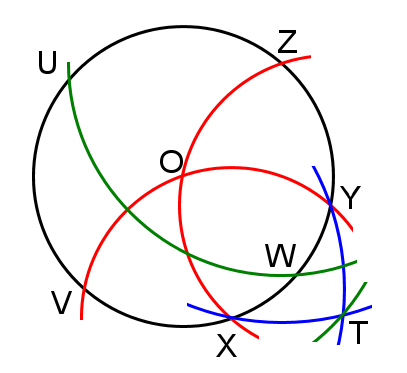
Dividing a given circle into four equal arcs given its centre
Nap4.png

Centred on any point X on circle C, draw an arc through O (the centre of C) which intersects C at points V and Y. Do the same centred on Y through O, intersecting C at X and Z. Note that the line segments OV, OX, OY, OZ, VX, XY, YZ have the same length, all distances being equal to the radius of the circle C.

Now draw an arc centred on V which goes through Y and an arc centred on Z which goes through X; call where these two arcs intersect T. Note that the distances VY and XZ are \( {\sqrt {3}} \) times the radius of the circle C.

Put the compass radius equal to the distance OT (\( {\sqrt {2}} \) times the radius of the circle C) and draw an arc centred on Z which intersects the circle C at U and W. UVWZ is a square and the arcs of C UV, VW, WZ, and ZU are each equal to a quarter of the circumference of C.
Finding the centre of a given circle

Let (C) be the circle, whose centre is to be found.[3]

Let A be a point on (C).

A circle (C1) centered at A meets (C) at B and B'.

Two circles (C2) centered at B and B', with radius AB, cross again at point C.

A circle (C3) centered at C with radius AC meets (C1) at D and D'.

Two circles (C4) centered at D and D' with radius AD meet at A, and at O, the sought center of (C).

Note: for this to work the radius of circle (C1) must be neither too small nor too large. More precisely, this radius must be between half and double of the radius of (C): if the radius is greater than the diameter of (C), (C1) will not intersect (C); if the radius is shorter than half the radius of (C), point C will be between A and O and (C3) will not intersect (C).
Proof

The idea behind the proof is to construct, with compass alone, the length b²/a when lengths a and b are known, and a/2 ≤ b ≤ 2a.

In the figure on the right, a circle of radius a is drawn, centred at O; on it a point A is chosen, from which points B and B' can be determined such that AB and AB' have a length of b. Point A' lies opposite A, but does not need to be constructed (it would require a straightedge); similarly point H is the (virtual) intersection of AA' and BB'. Point C can be determined from B and B', using circles of radius b.

Triangle ABA' has a right angle at B and BH is perpendicular to AA', so :

\( {\displaystyle {\frac {AH}{AB}}={\frac {AB}{AA'}}} \)

Therefore, \( {\displaystyle AH={\frac {b^{2}}{2a}}} \) and AC = b²/a.

In the above construction of the center, such a configuration appears twice :

points A, B and B' are on the circle (C), radius a
1 = r ; AB, AB', BC, and B'C are equal to b
1 = R, so \( {\displaystyle AC={\frac {R^{2}}{r}}}; \)
points A, D and D' are on the circle of centre C, radius \( {\displaystyle a_{2}={\frac {R^{2}}{r}}} \) ; DA, D'A, DO, and D'O are equal to b
2 = R, so \( {\displaystyle AO={\frac {R^{2}}{R^{2}/r}}=r} \) .

Therefore, O is the centre of circle (C).
Finding the middle of a given distance or of a line segment

Construction the middle of a distance or of a line segment only with a compass

Let |AD| be the distance, whose centre is to be found.[4]

Two circles (C1) centered at A and (C2) centered at D with radius |AD| meet at B and B'.

A circle (C3) centered at B' with radius |B'B| meets the circle (C2) at A'.

A circle (C4) centered at A' with radius |A'A| meets the circle (C1) at E and E'.

Two circles (C5) centered at E and (C6) centered at E' with radius |EA| meet at A and O. O is the sought center of |AD|.

The design principle can also be applied to a line segment AD.
The proof described above is also applicable for this design.

Note: Point A in design is equivalent to A in proof.
Therefore radius: (C2) ≙ (C) and points: O ≙ H, B ≙ B, D ≙ O and A' ≙ A'.