In 8-dimensional geometry, there are 256 uniform polytopes with B8 symmetry. There are two regular forms, the 8-orthoplex, and 8-cube with 16 and 256 vertices respectively. The 8-demicube is added with half the symmetry.
They can be visualized as symmetric orthographic projections in Coxeter planes of the B8 Coxeter group, and other subgroups.
Graphs
Symmetric orthographic projections of these 256 polytopes can be made in the B8, B7, B6, B5, B4, B3, B2, A7, A5, A3, Coxeter planes. Ak has [k+1] symmetry, and Bk has [2k] symmetry.
These 256 polytopes are each shown in these 10 symmetry planes, with vertices and edges drawn, and vertices colored by the number of overlapping vertices in each projective position.
| Element counts | Coxeter-Dynkin diagram Schläfli symbol Name |
||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| B8 [16] |
B7 [14] |
B6 [12] |
B5 [10] |
B4 [8] |
B3 [6] |
B2 [4] |
A7 [8] |
A5 [6] |
A3 [4] |
||
| 1 |  |
 |
 |
 |
 |
 |
 |
 |
 |
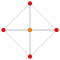 |
t0{3,3,3,3,3,3,4} 8-orthoplex Diacosipentacontahexazetton (ek) |
| 2 |  |
 |
 |
 |
 |
 |
 |
 |
 |
 |
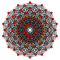
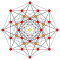
t1{3,3,3,3,3,3,4} Rectified 8-orthoplex Rectified diacosipentacontahexazetton (rek) |
| 3 |  |
 |
 |
 |
 |
 |
 |
 |
 |
 |
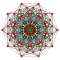
t2{3,3,3,3,3,3,4} Birectified 8-orthoplex Birectified diacosipentacontahexazetton (bark) |
| 4 |  |
 |
 |
 |
 |
 |
 |
 |
 |
 |
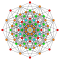
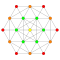
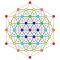
t3{3,3,3,3,3,3,4} Trirectified 8-orthoplex Trirectified diacosipentacontahexazetton (tark) |
| 5 |  |
 |
 |
 |
 |
 |
 |
 |
 |
 |
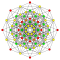
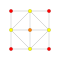
t3{4,3,3,3,3,3,3} Trirectified 8-cube Trirectified octeract (tro) |
| 6 |  |
 |
 |
 |
 |
 |
 |
 |
 |
 |
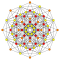
t2{4,3,3,3,3,3,3} Birectified 8-cube Birectified octeract (bro) |
| 7 |  |
 |
 |
 |
 |
 |
 |
 |
 |
 |
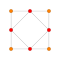
t1{4,3,3,3,3,3,3} Rectified 8-cube Rectified octeract (recto) |
| 8 |  |
 |
 |
 |
 |
 |
 |
 |
 |
 |
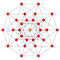
t0{4,3,3,3,3,3,3} 8-cube Octeract (octo) |
| 9 |  |
 |
 |
 |
 |
 |
 |
 |
 |
 |
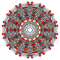
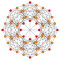
t0,1{3,3,3,3,3,3,4} Truncated 8-orthoplex Truncated diacosipentacontahexazetton (tek) |
| 10 |  |
 |
 |
 |
 |
 |
 |
 |
 |
 |
t0,2{3,3,3,3,3,3,4} Cantellated 8-orthoplex Small rhombated diacosipentacontahexazetton (srek) |
| 11 |  |
 |
 |
 |
 |
 |
 |
 |
 |
 |
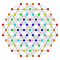
t1,2{3,3,3,3,3,3,4} Bitruncated 8-orthoplex Bitruncated diacosipentacontahexazetton (batek) |
| 12 |  |
 |
 |
 |
 |
 |
 |
 |
 |
 |
t0,3{3,3,3,3,3,3,4} Runcinated 8-orthoplex Small prismated diacosipentacontahexazetton (spek) |
| 13 |  |
 |
 |
 |
 |
 |
 |
 |
 |
 |
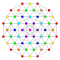
t1,3{3,3,3,3,3,3,4} Bicantellated 8-orthoplex Small birhombated diacosipentacontahexazetton (sabork) |
| 14 |  |
 |
 |
 |
 |
 |
 |
 |
 |
 |
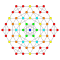
t2,3{3,3,3,3,3,3,4} Tritruncated 8-orthoplex Tritruncated diacosipentacontahexazetton (tatek) |
| 15 |  |
 |
 |
 |
 |
 |
 |
 |
 |
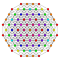
t0,4{3,3,3,3,3,3,4} Stericated 8-orthoplex Small cellated diacosipentacontahexazetton (scak) |
|
| 16 |  |
 |
 |
 |
 |
 |
 |
 |
 |
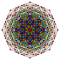
t1,4{3,3,3,3,3,3,4} Biruncinated 8-orthoplex Small biprismated diacosipentacontahexazetton (sabpek) |
|
| 17 |  |
 |
 |
 |
 |
 |
 |
 |
 |
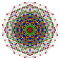
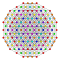
t2,4{3,3,3,3,3,3,4} Tricantellated 8-orthoplex Small trirhombated diacosipentacontahexazetton (satrek) |
|
| 18 |  |
 |
 |
 |
 |
 |
 |
 |
 |
 |
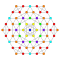
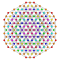
t3,4{4,3,3,3,3,3,3} Quadritruncated 8-cube Octeractidiacosipentacontahexazetton (oke) |
| 19 |  |
 |
 |
 |
 |
 |
 |
 |
 |
t0,5{3,3,3,3,3,3,4} Pentellated 8-orthoplex Small terated diacosipentacontahexazetton (setek) |
|
| 20 |  |
 |
 |
 |
 |
 |
 |
 |
 |
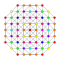 |
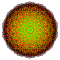
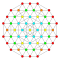
t1,5{3,3,3,3,3,3,4} Bistericated 8-orthoplex Small bicellated diacosipentacontahexazetton (sibcak) |
| 21 |  |
 |
 |
 |
 |
 |
 |
 |
 |
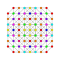 |
t2,5{4,3,3,3,3,3,3} Triruncinated 8-cube Small triprismato-octeractidiacosipentacontahexazetton (sitpoke) |
| 22 |  |
 |
 |
 |
 |
 |
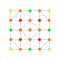 |
 |
 |
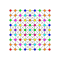 |
t2,4{4,3,3,3,3,3,3} Tricantellated 8-cube Small trirhombated octeract (satro) |
| 23 |  |
 |
 |
 |
 |
 |
 |
 |
 |
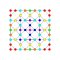 |
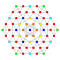
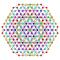
t2,3{4,3,3,3,3,3,3} Tritruncated 8-cube Tritruncated octeract (tato) |
| 24 |  |
 |
 |
 |
 |
 |
 |
 |
 |
 |
t0,6{3,3,3,3,3,3,4} Hexicated 8-orthoplex Small petated diacosipentacontahexazetton (supek) |
| 25 |  |
 |
 |
 |
 |
 |
 |
 |
 |
 |
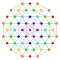
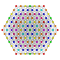
t1,6{4,3,3,3,3,3,3} Bipentellated 8-cube Small biteri-octeractidiacosipentacontahexazetton (sabtoke) |
| 26 |  |
 |
 |
 |
 |
 |
 |
 |
 |
 |
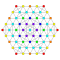
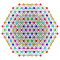
t1,5{4,3,3,3,3,3,3} Bistericated 8-cube Small bicellated octeract (sobco) |
| 27 |  |
 |
 |
 |
 |
 |
 |
 |
 |
 |
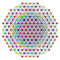
t1,4{4,3,3,3,3,3,3} Biruncinated 8-cube Small biprismated octeract (sabepo) |
| 28 |  |
 |
 |
 |
 |
 |
 |
 |
 |
 |
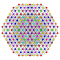
t1,3{4,3,3,3,3,3,3} Bicantellated 8-cube Small birhombated octeract (subro) |
| 29 |  |
 |
 |
 |
 |
 |
 |
 |
 |
 |
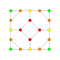
t1,2{4,3,3,3,3,3,3} Bitruncated 8-cube Bitruncated octeract (bato) |
| 30 |  |
 |
 |
 |
 |
 |
 |
 |
 |
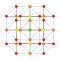 |
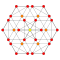
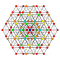
t0,7{4,3,3,3,3,3,3} Heptellated 8-cube Small exi-octeractidiacosipentacontahexazetton (saxoke) |
| 31 |  |
 |
 |
 |
 |
 |
 |
 |
 |
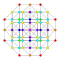 |
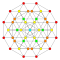
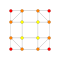
t0,6{4,3,3,3,3,3,3} Hexicated 8-cube Small petated octeract (supo) |
| 32 |  |
 |
 |
 |
 |
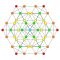 |
 |
 |
 |
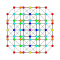 |
t0,5{4,3,3,3,3,3,3} Pentellated 8-cube Small terated octeract (soto) |
| 33 |  |
 |
 |
 |
 |
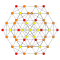 |
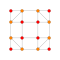 |
 |
 |
 |
t0,4{4,3,3,3,3,3,3} Stericated 8-cube Small cellated octeract (soco) |
| 34 |  |
 |
 |
 |
 |
 |
 |
 |
 |
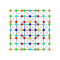 |
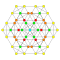
t0,3{4,3,3,3,3,3,3} Runcinated 8-cube Small prismated octeract (sopo) |
| 35 |  |
 |
 |
 |
 |
 |
 |
 |
 |
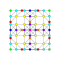 |
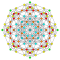
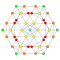
t0,2{4,3,3,3,3,3,3} Cantellated 8-cube Small rhombated octeract (soro) |
| 36 |  |
 |
 |
 |
 |
 |
 |
 |
 |
 |
t0,1{4,3,3,3,3,3,3} Truncated 8-cube Truncated octeract (tocto) |
| 37 |  |
 |
 |
 |
 |
 |
 |
 |
 |
 |
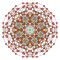
t0,1,2{3,3,3,3,3,3,4} Cantitruncated 8-orthoplex Great rhombated diacosipentacontahexazetton |
| 38 |  |
 |
 |
 |
 |
 |
 |
 |
 |
 |
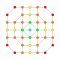
t0,1,3{3,3,3,3,3,3,4} Runcitruncated 8-orthoplex Prismatotruncated diacosipentacontahexazetton |
| 39 |  |
 |
 |
 |
 |
 |
 |
 |
 |
 |
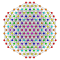
t0,2,3{3,3,3,3,3,3,4} Runcicantellated 8-orthoplex Prismatorhombated diacosipentacontahexazetton |
| 40 |  |
 |
 |
 |
 |
 |
 |
 |
 |
 |
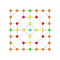
t1,2,3{3,3,3,3,3,3,4} Bicantitruncated 8-orthoplex Great birhombated diacosipentacontahexazetton |
| 41 |  |
 |
 |
 |
 |
 |
 |
 |
 |
 |
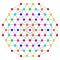
t0,1,4{3,3,3,3,3,3,4} Steritruncated 8-orthoplex Cellitruncated diacosipentacontahexazetton |
| 42 |  |
 |
 |
 |
 |
 |
 |
 |
 |
 |
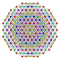
t0,2,4{3,3,3,3,3,3,4} Stericantellated 8-orthoplex Cellirhombated diacosipentacontahexazetton |
| 43 |  |
 |
 |
 |
 |
 |
 |
 |
 |
 |
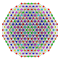
t1,2,4{3,3,3,3,3,3,4} Biruncitruncated 8-orthoplex Biprismatotruncated diacosipentacontahexazetton |
| 44 |  |
 |
 |
 |
 |
 |
 |
 |
 |
 |
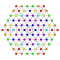
t0,3,4{3,3,3,3,3,3,4} Steriruncinated 8-orthoplex Celliprismated diacosipentacontahexazetton |
| 45 |  |
 |
 |
 |
 |
 |
 |
 |
 |
 |
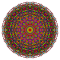
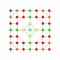
t1,3,4{3,3,3,3,3,3,4} Biruncicantellated 8-orthoplex Biprismatorhombated diacosipentacontahexazetton |
| 46 |  |
 |
 |
 |
 |
 |
 |
 |
 |
 |
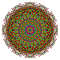
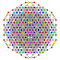
t2,3,4{3,3,3,3,3,3,4} Tricantitruncated 8-orthoplex Great trirhombated diacosipentacontahexazetton |
| 47 |  |
 |
 |
 |
 |
 |
 |
 |
 |
 |
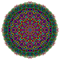
t0,1,5{3,3,3,3,3,3,4} Pentitruncated 8-orthoplex Teritruncated diacosipentacontahexazetton |
| 48 |  |
 |
 |
 |
 |
 |
 |
 |
 |
 |
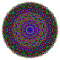
t0,2,5{3,3,3,3,3,3,4} Penticantellated 8-orthoplex Terirhombated diacosipentacontahexazetton |
| 49 |  |
 |
 |
 |
 |
 |
 |
 |
 |
 |
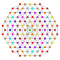
t1,2,5{3,3,3,3,3,3,4} Bisteritruncated 8-orthoplex Bicellitruncated diacosipentacontahexazetton |
| 50 |  |
 |
 |
 |
 |
 |
 |
 |
 |
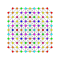 |
t0,3,5{3,3,3,3,3,3,4} Pentiruncinated 8-orthoplex Teriprismated diacosipentacontahexazetton |
| 51 | 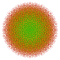 |
 |
 |
 |
 |
 |
 |
 |
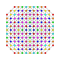 |
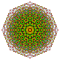
t1,3,5{3,3,3,3,3,3,4} Bistericantellated 8-orthoplex Bicellirhombated diacosipentacontahexazetton |
|
| 52 |  |
 |
 |
 |
 |
 |
 |
 |
 |
 |
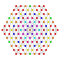
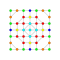
t2,3,5{3,3,3,3,3,3,4} Triruncitruncated 8-orthoplex Triprismatotruncated diacosipentacontahexazetton |
| 53 |  |
 |
 |
 |
 |
 |
 |
 |
 |
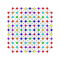 |
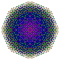
t0,4,5{3,3,3,3,3,3,4} Pentistericated 8-orthoplex Tericellated diacosipentacontahexazetton |
| 54 |  |
 |
 |
 |
 |
 |
 |
 |
 |
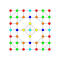
 |
t1,4,5{3,3,3,3,3,3,4} Bisteriruncinated 8-orthoplex Bicelliprismated diacosipentacontahexazetton |
| 55 |  |
 |
 |
 |
 |
 |
 |
 |
 |
 |
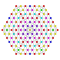
t2,3,5{4,3,3,3,3,3,3} Triruncitruncated 8-cube Triprismatotruncated octeract |
| 56 |  |
 |
 |
 |
 |
 |
 |
 |
 |
 |
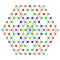
t2,3,4{4,3,3,3,3,3,3} Tricantitruncated 8-cube Great trirhombated octeract |
| 57 |  |
 |
 |
 |
 |
 |
 |
 |
 |
 |
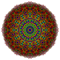
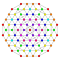
t0,1,6{3,3,3,3,3,3,4} Hexitruncated 8-orthoplex Petitruncated diacosipentacontahexazetton |
| 58 |  |
 |
 |
 |
 |
 |
 |
 |
 |
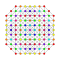 |
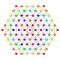
t0,2,6{3,3,3,3,3,3,4} Hexicantellated 8-orthoplex Petirhombated diacosipentacontahexazetton |
| 59 |  |
 |
 |
 |
 |
 |
 |
 |
 |
 |
t1,2,6{3,3,3,3,3,3,4} Bipentitruncated 8-orthoplex Biteritruncated diacosipentacontahexazetton |
| 60 |  |
 |
 |
 |
 |
 |
 |
 |
 |
t0,3,6{3,3,3,3,3,3,4} Hexiruncinated 8-orthoplex Petiprismated diacosipentacontahexazetton |
|
| 61 |  |
 |
 |
 |
 |
 |
 |
 |
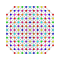 |
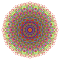
t1,3,6{3,3,3,3,3,3,4} Bipenticantellated 8-orthoplex Biterirhombated diacosipentacontahexazetton |
|
| 62 |  |
 |
 |
 |
 |
 |
 |
 |
 |
t1,4,5{4,3,3,3,3,3,3} Bisteriruncinated 8-cube Bicelliprismated octeract |
|
| 63 |  |
 |
 |
 |
 |
 |
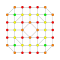 |
 |
 |
 |
t0,4,6{3,3,3,3,3,3,4} Hexistericated 8-orthoplex Peticellated diacosipentacontahexazetton |
| 64 |  |
 |
 |
 |
 |
 |
 |
 |
 |
t1,3,6{4,3,3,3,3,3,3} Bipenticantellated 8-cube Biterirhombated octeract |
|
| 65 |  |
 |
 |
 |
 |
 |
 |
 |
 |
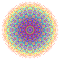
t1,3,5{4,3,3,3,3,3,3} Bistericantellated 8-cube Bicellirhombated octeract |
|
| 66 |  |
 |
 |
 |
 |
 |
 |
 |
 |
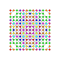 |
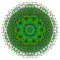
t1,3,4{4,3,3,3,3,3,3} Biruncicantellated 8-cube Biprismatorhombated octeract |
| 67 |  |
 |
 |
 |
 |
 |
 |
 |
 |
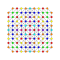 |
t0,5,6{3,3,3,3,3,3,4} Hexipentellated 8-orthoplex Petiterated diacosipentacontahexazetton |
| 68 |  |
 |
 |
 |
 |
 |
 |
 |
 |
 |
t1,2,6{4,3,3,3,3,3,3} Bipentitruncated 8-cube Biteritruncated octeract |
| 69 |  |
 |
 |
 |
 |
 |
 |
 |
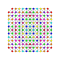 |
t1,2,5{4,3,3,3,3,3,3} Bisteritruncated 8-cube Bicellitruncated octeract |
|
| 70 |  |
 |
 |
 |
 |
 |
 |
 |
 |
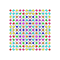 |
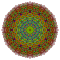
t1,2,4{4,3,3,3,3,3,3} Biruncitruncated 8-cube Biprismatotruncated octeract |
| 71 |  |
 |
 |
 |
 |
 |
 |
 |
 |
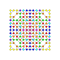 |
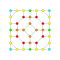
t1,2,3{4,3,3,3,3,3,3} Bicantitruncated 8-cube Great birhombated octeract |
| 72 |  |
 |
 |
 |
 |
 |
 |
 |
 |
 |
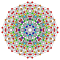
t0,1,7{3,3,3,3,3,3,4} Heptitruncated 8-orthoplex Exitruncated diacosipentacontahexazetton |
| 73 |  |
 |
 |
 |
 |
 |
 |
 |
 |
 |
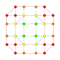
t0,2,7{3,3,3,3,3,3,4} Hepticantellated 8-orthoplex Exirhombated diacosipentacontahexazetton |
| 74 |  |
 |
 |
 |
 |
 |
 |
 |
 |
 |
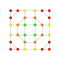
t0,5,6{4,3,3,3,3,3,3} Hexipentellated 8-cube Petiterated octeract |
| 75 |  |
 |
 |
 |
 |
 |
 |
 |
 |
 |
t0,3,7{3,3,3,3,3,3,4} Heptiruncinated 8-orthoplex Exiprismated diacosipentacontahexazetton |
| 76 |  |
 |
 |
 |
 |
 |
 |
 |
 |
 |
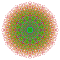
t0,4,6{4,3,3,3,3,3,3} Hexistericated 8-cube Peticellated octeract |
| 77 |  |
 |
 |
 |
 |
 |
 |
 |
 |
 |
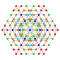
t0,4,5{4,3,3,3,3,3,3} Pentistericated 8-cube Tericellated octeract |
| 78 |  |
 |
 |
 |
 |
 |
 |
 |
 |
 |
t0,3,7{4,3,3,3,3,3,3} Heptiruncinated 8-cube Exiprismated octeract |
| 79 | 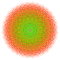 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
t0,3,6{4,3,3,3,3,3,3} Hexiruncinated 8-cube Petiprismated octeract |
| 80 |  |
 |
 |
 |
 |
 |
 |
 |
 |
 |
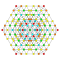
t0,3,5{4,3,3,3,3,3,3} Pentiruncinated 8-cube Teriprismated octeract |
| 81 |  |
 |
 |
 |
 |
 |
 |
 |
 |
 |
t0,3,4{4,3,3,3,3,3,3} Steriruncinated 8-cube Celliprismated octeract |
| 82 | 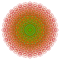 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
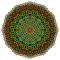
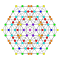
t0,2,7{4,3,3,3,3,3,3} Hepticantellated 8-cube Exirhombated octeract |
| 83 |  |
 |
 |
 |
 |
 |
 |
 |
 |
 |
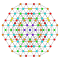
t0,2,6{4,3,3,3,3,3,3} Hexicantellated 8-cube Petirhombated octeract |
| 84 |  |
 |
 |
 |
 |
 |
 |
 |
 |
 |
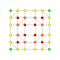
t0,2,5{4,3,3,3,3,3,3} Penticantellated 8-cube Terirhombated octeract |
| 85 |  |
 |
 |
 |
 |
 |
 |
 |
 |
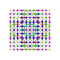 |
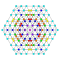
t0,2,4{4,3,3,3,3,3,3} Stericantellated 8-cube Cellirhombated octeract |
| 86 |  |
 |
 |
 |
 |
 |
 |
 |
 |
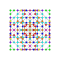 |
t0,2,3{4,3,3,3,3,3,3} Runcicantellated 8-cube Prismatorhombated octeract |
| 87 |  |
 |
 |
 |
 |
 |
 |
 |
 |
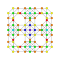 |
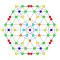
t0,1,7{4,3,3,3,3,3,3} Heptitruncated 8-cube Exitruncated octeract |
| 88 |  |
 |
 |
 |
 |
 |
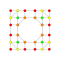 |
 |
 |
 |
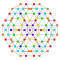
t0,1,6{4,3,3,3,3,3,3} Hexitruncated 8-cube Petitruncated octeract |
| 89 |  |
 |
 |
 |
 |
 |
 |
 |
 |
 |
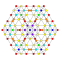
t0,1,5{4,3,3,3,3,3,3} Pentitruncated 8-cube Teritruncated octeract |
| 90 |  |
 |
 |
 |
 |
 |
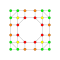 |
 |
 |
 |
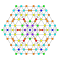
t0,1,4{4,3,3,3,3,3,3} Steritruncated 8-cube Cellitruncated octeract |
| 91 |  |
 |
 |
 |
 |
 |
 |
 |
 |
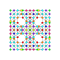 |
t0,1,3{4,3,3,3,3,3,3} Runcitruncated 8-cube Prismatotruncated octeract |
| 92 |  |
 |
 |
 |
 |
 |
 |
 |
 |
 |
t0,1,2{4,3,3,3,3,3,3} Cantitruncated 8-cube Great rhombated octeract |
| 93 |  |
 |
 |
 |
 |
 |
 |
 |
 |
 |
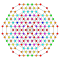
t0,1,2,3{3,3,3,3,3,3,4} Runcicantitruncated 8-orthoplex Great prismated diacosipentacontahexazetton |
| 94 |  |
 |
 |
 |
 |
 |
 |
 |
 |
 |
t0,1,2,4{3,3,3,3,3,3,4} Stericantitruncated 8-orthoplex Celligreatorhombated diacosipentacontahexazetton |
| 95 |  |
 |
 |
 |
 |
 |
 |
 |
 |
 |
t0,1,3,4{3,3,3,3,3,3,4} Steriruncitruncated 8-orthoplex Celliprismatotruncated diacosipentacontahexazetton |
| 96 |  |
 |
 |
 |
 |
 |
 |
 |
 |
 |
t0,2,3,4{3,3,3,3,3,3,4} Steriruncicantellated 8-orthoplex Celliprismatorhombated diacosipentacontahexazetton |
| 97 |  |
 |
 |
 |
 |
 |
 |
 |
 |
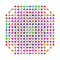 |
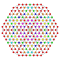
t1,2,3,4{3,3,3,3,3,3,4} Biruncicantitruncated 8-orthoplex Great biprismated diacosipentacontahexazetton |
| 98 | 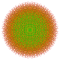 |
 |
 |
 |
 |
 |
 |
 |
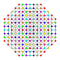 |
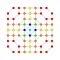
t0,1,2,5{3,3,3,3,3,3,4} Penticantitruncated 8-orthoplex Terigreatorhombated diacosipentacontahexazetton |
|
| 99 |  |
 |
 |
 |
 |
 |
 |
 |
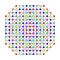 |
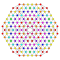
t0,1,3,5{3,3,3,3,3,3,4} Pentiruncitruncated 8-orthoplex Teriprismatotruncated diacosipentacontahexazetton |
|
| 100 |  |
 |
 |
 |
 |
 |
 |
 |
 |
t0,2,3,5{3,3,3,3,3,3,4} Pentiruncicantellated 8-orthoplex Teriprismatorhombated diacosipentacontahexazetton |
|
| 101 |  |
 |
 |
 |
 |
 |
 |
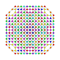 |
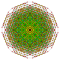
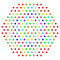
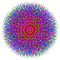
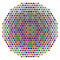
t1,2,3,5{3,3,3,3,3,3,4} Bistericantitruncated 8-orthoplex Bicelligreatorhombated diacosipentacontahexazetton |
||
| 102 |  |
 |
 |
 |
 |
 |
 |
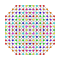 |
t0,1,4,5{3,3,3,3,3,3,4} Pentisteritruncated 8-orthoplex Tericellitruncated diacosipentacontahexazetton |
||
| 103 | 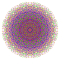 |
 |
 |
 |
 |
 |
 |
 |
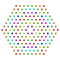
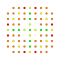
t0,2,4,5{3,3,3,3,3,3,4} Pentistericantellated 8-orthoplex Tericellirhombated diacosipentacontahexazetton |
||
| 104 |  |
 |
 |
 |
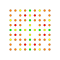 |
 |
 |
 |
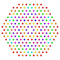
t1,2,4,5{3,3,3,3,3,3,4} Bisteriruncitruncated 8-orthoplex Bicelliprismatotruncated diacosipentacontahexazetton |
||
| 105 |  |
 |
 |
 |
 |
 |
 |
 |
t0,3,4,5{3,3,3,3,3,3,4} Pentisteriruncinated 8-orthoplex Tericelliprismated diacosipentacontahexazetton |
||
| 106 |  |
 |
 |
 |
 |
 |
 |
 |
t1,3,4,5{3,3,3,3,3,3,4} Bisteriruncicantellated 8-orthoplex Bicelliprismatorhombated diacosipentacontahexazetton |
||
| 107 | 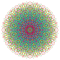 |
 |
 |
 |
 |
 |
 |
 |
t2,3,4,5{4,3,3,3,3,3,3} Triruncicantitruncated 8-cube Great triprismato-octeractidiacosipentacontahexazetton |
||
| 108 |  |
 |
 |
 |
 |
 |
 |
 |
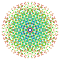
t0,1,2,6{3,3,3,3,3,3,4} Hexicantitruncated 8-orthoplex Petigreatorhombated diacosipentacontahexazetton |
||
| 109 |  |
 |
 |
 |
 |
 |
 |
 |
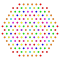
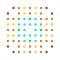
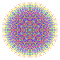
t0,1,3,6{3,3,3,3,3,3,4} Hexiruncitruncated 8-orthoplex Petiprismatotruncated diacosipentacontahexazetton |
||
| 110 |  |
 |
 |
 |
 |
 |
 |
 |
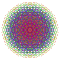
t0,2,3,6{3,3,3,3,3,3,4} Hexiruncicantellated 8-orthoplex Petiprismatorhombated diacosipentacontahexazetton |
||
| 111 | 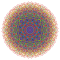 |
 |
 |
 |
 |
 |
 |
 |
t1,2,3,6{3,3,3,3,3,3,4} Bipenticantitruncated 8-orthoplex Biterigreatorhombated diacosipentacontahexazetton |
||
| 112 | 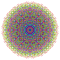 |
 |
 |
 |
 |
 |
 |
 |
t0,1,4,6{3,3,3,3,3,3,4} Hexisteritruncated 8-orthoplex Peticellitruncated diacosipentacontahexazetton |
||
| 113 |  |
 |
 |
 |
 |
 |
 |
 |
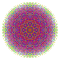
t0,2,4,6{3,3,3,3,3,3,4} Hexistericantellated 8-orthoplex Peticellirhombated diacosipentacontahexazetton |
||
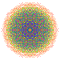
| 114 |  |
 |
 |
 |
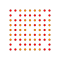 |
 |
 |
 |
t1,2,4,6{3,3,3,3,3,3,4} Bipentiruncitruncated 8-orthoplex Biteriprismatotruncated diacosipentacontahexazetton |
||
| 115 |  |
 |
 |
 |
 |
 |
 |
 |
t0,3,4,6{3,3,3,3,3,3,4} Hexisteriruncinated 8-orthoplex Peticelliprismated diacosipentacontahexazetton |
||
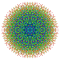
| 116 |  |
 |
 |
 |
 |
 |
 |
 |
t1,3,4,6{4,3,3,3,3,3,3} Bipentiruncicantellated 8-cube Biteriprismatorhombi-octeractidiacosipentacontahexazetton |
||
| 117 | 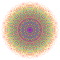 |
 |
 |
 |
 |
 |
 |
 |
t1,3,4,5{4,3,3,3,3,3,3} Bisteriruncicantellated 8-cube Bicelliprismatorhombated octeract |
||
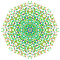
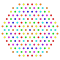
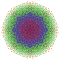
| 118 |  |
 |
 |
 |
 |
 |
 |
 |
t0,1,5,6{3,3,3,3,3,3,4} Hexipentitruncated 8-orthoplex Petiteritruncated diacosipentacontahexazetton |
||
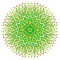
| 119 |  |
 |
 |
 |
 |
 |
 |
 |
t0,2,5,6{3,3,3,3,3,3,4} Hexipenticantellated 8-orthoplex Petiterirhombated diacosipentacontahexazetton |
||
| 120 | 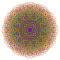 |
 |
 |
 |
 |
 |
 |
 |
t1,2,5,6{4,3,3,3,3,3,3} Bipentisteritruncated 8-cube Bitericellitrunki-octeractidiacosipentacontahexazetton |
||
| 121 |  |
 |
 |
 |
 |
 |
 |
 |
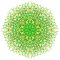
t0,3,5,6{3,3,3,3,3,3,4} Hexipentiruncinated 8-orthoplex Petiteriprismated diacosipentacontahexazetton |
||
| 122 |  |
 |
 |
 |
 |
 |
 |
 |
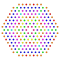
t1,2,4,6{4,3,3,3,3,3,3} Bipentiruncitruncated 8-cube Biteriprismatotruncated octeract |
||
| 123 |  |
 |
 |
 |
 |
 |
 |
 |
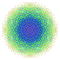
t1,2,4,5{4,3,3,3,3,3,3} Bisteriruncitruncated 8-cube Bicelliprismatotruncated octeract |
||
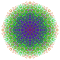
| 124 | 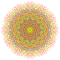 |
 |
 |
 |
 |
 |
 |
 |
t0,4,5,6{3,3,3,3,3,3,4} Hexipentistericated 8-orthoplex Petitericellated diacosipentacontahexazetton |
||
| 125 |  |
 |
 |
 |
 |
 |
 |
 |
t1,2,3,6{4,3,3,3,3,3,3} Bipenticantitruncated 8-cube Biterigreatorhombated octeract |
||
| 126 |  |
 |
 |
 |
 |
 |
 |
 |
t1,2,3,5{4,3,3,3,3,3,3} Bistericantitruncated 8-cube Bicelligreatorhombated octeract |
||
| 127 | 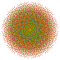 |
 |
 |
 |
 |
 |
 |
 |
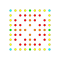
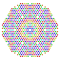
t1,2,3,4{4,3,3,3,3,3,3} Biruncicantitruncated 8-cube Great biprismated octeract |
||
| 128 |  |
 |
 |
 |
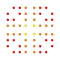 |
 |
 |
 |
t0,1,2,7{3,3,3,3,3,3,4} Hepticantitruncated 8-orthoplex Exigreatorhombated diacosipentacontahexazetton |
||
| 129 |  |
 |
 |
 |
 |
 |
 |
 |
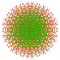
t0,1,3,7{3,3,3,3,3,3,4} Heptiruncitruncated 8-orthoplex Exiprismatotruncated diacosipentacontahexazetton |
||
| 130 |  |
 |
 |
 |
 |
 |
 |
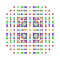 |
t0,2,3,7{3,3,3,3,3,3,4} Heptiruncicantellated 8-orthoplex Exiprismatorhombated diacosipentacontahexazetton |
||
| 131 |  |
 |
 |
 |
 |
 |
 |
 |
t0,4,5,6{4,3,3,3,3,3,3} Hexipentistericated 8-cube Petitericellated octeract |
||
| 132 |  |
 |
 |
 |
 |
 |
 |
 |
t0,1,4,7{3,3,3,3,3,3,4} Heptisteritruncated 8-orthoplex Exicellitruncated diacosipentacontahexazetton |
||
| 133 |  |
 |
 |
 |
 |
 |
 |
 |
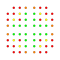
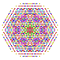
t0,2,4,7{3,3,3,3,3,3,4} Heptistericantellated 8-orthoplex Exicellirhombated diacosipentacontahexazetton |
||
| 134 | 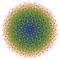 |
 |
 |
 |
 |
 |
 |
 |
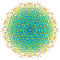
t0,3,5,6{4,3,3,3,3,3,3} Hexipentiruncinated 8-cube Petiteriprismated octeract |
||
| 135 |  |
 |
 |
 |
 |
 |
 |
 |
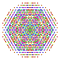
t0,3,4,7{4,3,3,3,3,3,3} Heptisteriruncinated 8-cube Exicelliprismato-octeractidiacosipentacontahexazetton |
||
| 136 |  |
 |
 |
 |
 |
 |
 |
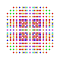 |
t0,3,4,6{4,3,3,3,3,3,3} Hexisteriruncinated 8-cube Peticelliprismated octeract |
||
| 137 |  |
 |
 |
 |
 |
 |
 |
 |
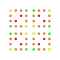
t0,3,4,5{4,3,3,3,3,3,3} Pentisteriruncinated 8-cube Tericelliprismated octeract |
||
| 138 | 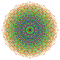 |
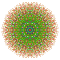 |
 |
 |
 |
 |
 |
 |
t0,1,5,7{3,3,3,3,3,3,4} Heptipentitruncated 8-orthoplex Exiteritruncated diacosipentacontahexazetton |
||
| 139 | 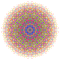 |
 |
 |
 |
 |
 |
 |
 |
t0,2,5,7{4,3,3,3,3,3,3} Heptipenticantellated 8-cube Exiterirhombi-octeractidiacosipentacontahexazetton |
||
| 140 | 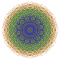 |
 |
 |
 |
 |
 |
 |
 |
t0,2,5,6{4,3,3,3,3,3,3} Hexipenticantellated 8-cube Petiterirhombated octeract |
||
| 141 |  |
 |
 |
 |
 |
 |
 |
 |
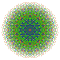
t0,2,4,7{4,3,3,3,3,3,3} Heptistericantellated 8-cube Exicellirhombated octeract |
||
| 142 | 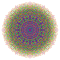 |
 |
 |
 |
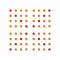 |
 |
 |
 |
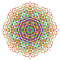
t0,2,4,6{4,3,3,3,3,3,3} Hexistericantellated 8-cube Peticellirhombated octeract |
||
| 143 |  |
 |
 |
 |
 |
 |
 |
 |
t0,2,4,5{4,3,3,3,3,3,3} Pentistericantellated 8-cube Tericellirhombated octeract |
||
| 144 | 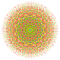 |
 |
 |
 |
 |
 |
 |
 |
t0,2,3,7{4,3,3,3,3,3,3} Heptiruncicantellated 8-cube Exiprismatorhombated octeract |
||
| 145 |  |
 |
 |
 |
 |
 |
 |
 |
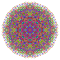
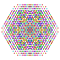
t0,2,3,6{4,3,3,3,3,3,3} Hexiruncicantellated 8-cube Petiprismatorhombated octeract |
||
| 146 |  |
 |
 |
 |
 |
 |
 |
 |
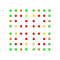
t0,2,3,5{4,3,3,3,3,3,3} Pentiruncicantellated 8-cube Teriprismatorhombated octeract |
||
| 147 |  |
 |
 |
 |
 |
 |
 |
 |
t0,2,3,4{4,3,3,3,3,3,3} Steriruncicantellated 8-cube Celliprismatorhombated octeract |
||
| 148 |  |
 |
 |
 |
 |
 |
 |
 |
t0,1,6,7{4,3,3,3,3,3,3} Heptihexitruncated 8-cube Exipetitrunki-octeractidiacosipentacontahexazetton |
||
| 149 | 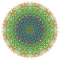 |
 |
 |
 |
 |
 |
 |
 |
t0,1,5,7{4,3,3,3,3,3,3} Heptipentitruncated 8-cube Exiteritruncated octeract |
||
| 150 |  |
 |
 |
 |
 |
 |
 |
 |
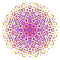
t0,1,5,6{4,3,3,3,3,3,3} Hexipentitruncated 8-cube Petiteritruncated octeract |
||
| 151 |  |
 |
 |
 |
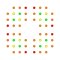 |
 |
 |
 |
t0,1,4,7{4,3,3,3,3,3,3} Heptisteritruncated 8-cube Exicellitruncated octeract |
||
| 152 |  |
 |
 |
 |
 |
 |
 |
 |
t0,1,4,6{4,3,3,3,3,3,3} Hexisteritruncated 8-cube Peticellitruncated octeract |
||
| 153 |  |
 |
 |
 |
 |
 |
 |
 |
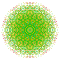
t0,1,4,5{4,3,3,3,3,3,3} Pentisteritruncated 8-cube Tericellitruncated octeract |
||
| 154 |  |
 |
 |
 |
 |
 |
 |
 |
t0,1,3,7{4,3,3,3,3,3,3} Heptiruncitruncated 8-cube Exiprismatotruncated octeract |
||
| 155 |  |
 |
 |
 |
 |
 |
 |
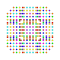 |
t0,1,3,6{4,3,3,3,3,3,3} Hexiruncitruncated 8-cube Petiprismatotruncated octeract |
||
| 156 |  |
 |
 |
 |
 |
 |
 |
 |
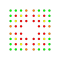
t0,1,3,5{4,3,3,3,3,3,3} Pentiruncitruncated 8-cube Teriprismatotruncated octeract |
||
| 157 |  |
 |
 |
 |
 |
 |
 |
 |
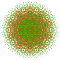
t0,1,3,4{4,3,3,3,3,3,3} Steriruncitruncated 8-cube Celliprismatotruncated octeract |
||
| 158 |  |
 |
 |
 |
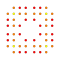 |
 |
 |
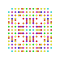 |
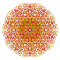
t0,1,2,7{4,3,3,3,3,3,3} Hepticantitruncated 8-cube Exigreatorhombated octeract |
||
| 159 |  |
 |
 |
 |
 |
 |
 |
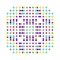 |
t0,1,2,6{4,3,3,3,3,3,3} Hexicantitruncated 8-cube Petigreatorhombated octeract |
||
| 160 |  |
 |
 |
 |
 |
 |
 |
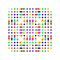 |
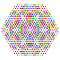
t0,1,2,5{4,3,3,3,3,3,3} Penticantitruncated 8-cube Terigreatorhombated octeract |
||
| 161 |  |
 |
 |
 |
 |
 |
 |
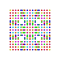 |
t0,1,2,4{4,3,3,3,3,3,3} Stericantitruncated 8-cube Celligreatorhombated octeract |
||
| 162 |  |
 |
 |
 |
 |
 |
 |
 |
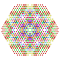
t0,1,2,3{4,3,3,3,3,3,3} Runcicantitruncated 8-cube Great prismated octeract |
||
| 163 |  |
 |
 |
 |
 |
 |
 |
 |
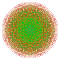
t0,1,2,3,4{3,3,3,3,3,3,4} Steriruncicantitruncated 8-orthoplex Great cellated diacosipentacontahexazetton |
||
| 164 |  |
 |
 |
 |
 |
 |
 |
 |
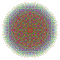
t0,1,2,3,5{3,3,3,3,3,3,4} Pentiruncicantitruncated 8-orthoplex Terigreatoprismated diacosipentacontahexazetton |
||
| 165 |  |
 |
 |
 |
 |
 |
 |
 |
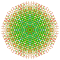
t0,1,2,4,5{3,3,3,3,3,3,4} Pentistericantitruncated 8-orthoplex Tericelligreatorhombated diacosipentacontahexazetton |
||
| 166 |  |
 |
 |
 |
 |
 |
 |
 |
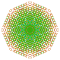
t0,1,3,4,5{3,3,3,3,3,3,4} Pentisteriruncitruncated 8-orthoplex Tericelliprismatotruncated diacosipentacontahexazetton |
||
| 167 |  |
 |
 |
 |
 |
 |
 |
 |
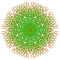
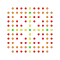
t0,2,3,4,5{3,3,3,3,3,3,4} Pentisteriruncicantellated 8-orthoplex Tericelliprismatorhombated diacosipentacontahexazetton |
||
| 168 |  |
 |
 |
 |
 |
 |
 |
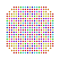 |
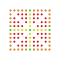
t1,2,3,4,5{3,3,3,3,3,3,4} Bisteriruncicantitruncated 8-orthoplex Great bicellated diacosipentacontahexazetton |
||
| 169 |  |
 |
 |
 |
 |
 |
 |
 |
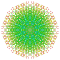
t0,1,2,3,6{3,3,3,3,3,3,4} Hexiruncicantitruncated 8-orthoplex Petigreatoprismated diacosipentacontahexazetton |
||
| 170 |  |
 |
 |
 |
 |
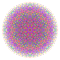 |
 |
 |
t0,1,2,4,6{3,3,3,3,3,3,4} Hexistericantitruncated 8-orthoplex Peticelligreatorhombated diacosipentacontahexazetton |
||
| 171 | 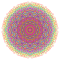 |
 |
 |
 |
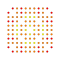 |
 |
 |
 |
t0,1,3,4,6{3,3,3,3,3,3,4} Hexisteriruncitruncated 8-orthoplex Peticelliprismatotruncated diacosipentacontahexazetton |
||
| 172 |  |
 |
 |
 |
 |
 |
 |
 |
t0,2,3,4,6{3,3,3,3,3,3,4} Hexisteriruncicantellated 8-orthoplex Peticelliprismatorhombated diacosipentacontahexazetton |
||
| 173 |  |
 |
 |
 |
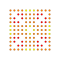 |
 |
 |
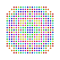 |
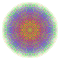
t1,2,3,4,6{3,3,3,3,3,3,4} Bipentiruncicantitruncated 8-orthoplex Biterigreatoprismated diacosipentacontahexazetton |
||
| 174 |  |
 |
 |
 |
 |
 |
 |
 |
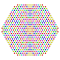
t0,1,2,5,6{3,3,3,3,3,3,4} Hexipenticantitruncated 8-orthoplex Petiterigreatorhombated diacosipentacontahexazetton |
||
| 175 | 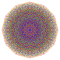 |
 |
 |
 |
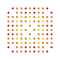 |
 |
 |
 |
t0,1,3,5,6{3,3,3,3,3,3,4} Hexipentiruncitruncated 8-orthoplex Petiteriprismatotruncated diacosipentacontahexazetton |
||
| 176 | 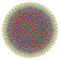 |
 |
 |
 |
 |
 |
 |
 |
t0,2,3,5,6{3,3,3,3,3,3,4} Hexipentiruncicantellated 8-orthoplex Petiteriprismatorhombated diacosipentacontahexazetton |
||
| 177 | 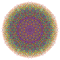 |
 |
 |
 |
 |
 |
 |
 |
t1,2,3,5,6{3,3,3,3,3,3,4} Bipentistericantitruncated 8-orthoplex Bitericelligreatorhombated diacosipentacontahexazetton |
||
| 178 |  |
 |
 |
 |
 |
 |
 |
 |
t0,1,4,5,6{3,3,3,3,3,3,4} Hexipentisteritruncated 8-orthoplex Petitericellitruncated diacosipentacontahexazetton |
||
| 179 |  |
 |
 |
 |
 |
 |
 |
 |
t0,2,4,5,6{3,3,3,3,3,3,4} Hexipentistericantellated 8-orthoplex Petitericellirhombated diacosipentacontahexazetton |
||
| 180 | 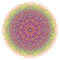 |
 |
 |
 |
 |
 |
 |
 |
t1,2,3,5,6{4,3,3,3,3,3,3} Bipentistericantitruncated 8-cube Bitericelligreatorhombated octeract |
||
| 181 |  |
 |
 |
 |
 |
 |
 |
 |
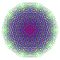
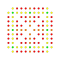
t0,3,4,5,6{3,3,3,3,3,3,4} Hexipentisteriruncinated 8-orthoplex Petitericelliprismated diacosipentacontahexazetton |
||
| 182 |  |
 |
 |
 |
 |
 |
 |
 |
t1,2,3,4,6{4,3,3,3,3,3,3} Bipentiruncicantitruncated 8-cube Biterigreatoprismated octeract |
||
| 183 |  |
 |
 |
 |
 |
 |
 |
 |
t1,2,3,4,5{4,3,3,3,3,3,3} Bisteriruncicantitruncated 8-cube Great bicellated octeract |
||
| 184 |  |
 |
 |
 |
 |
 |
 |
 |
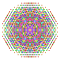
t0,1,2,3,7{3,3,3,3,3,3,4} Heptiruncicantitruncated 8-orthoplex Exigreatoprismated diacosipentacontahexazetton |
||
| 185 | 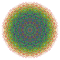 |
 |
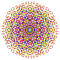 |
 |
 |
 |
 |
 |
t0,1,2,4,7{3,3,3,3,3,3,4} Heptistericantitruncated 8-orthoplex Exicelligreatorhombated diacosipentacontahexazetton |
||
| 186 |  |
 |
 |
 |
 |
 |
 |
 |
t0,1,3,4,7{3,3,3,3,3,3,4} Heptisteriruncitruncated 8-orthoplex Exicelliprismatotruncated diacosipentacontahexazetton |
||
| 187 |  |
 |
 |
 |
 |
 |
 |
 |
t0,2,3,4,7{3,3,3,3,3,3,4} Heptisteriruncicantellated 8-orthoplex Exicelliprismatorhombated diacosipentacontahexazetton |
||
| 188 |  |
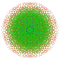 |
 |
 |
 |
 |
 |
 |
t0,3,4,5,6{4,3,3,3,3,3,3} Hexipentisteriruncinated 8-cube Petitericelliprismated octeract |
||
| 189 | 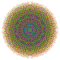 |
 |
 |
 |
 |
 |
 |
 |
t0,1,2,5,7{3,3,3,3,3,3,4} Heptipenticantitruncated 8-orthoplex Exiterigreatorhombated diacosipentacontahexazetton |
||
| 190 | 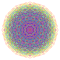 |
 |
 |
 |
 |
 |
 |
 |
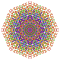
t0,1,3,5,7{3,3,3,3,3,3,4} Heptipentiruncitruncated 8-orthoplex Exiteriprismatotruncated diacosipentacontahexazetton |
||
| 191 |  |
 |
 |
 |
 |
 |
 |
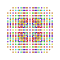 |
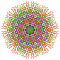
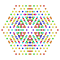
t0,2,3,5,7{3,3,3,3,3,3,4} Heptipentiruncicantellated 8-orthoplex Exiteriprismatorhombated diacosipentacontahexazetton |
||
| 192 |  |
 |
 |
 |
 |
 |
 |
 |
t0,2,4,5,6{4,3,3,3,3,3,3} Hexipentistericantellated 8-cube Petitericellirhombated octeract |
||
| 193 | 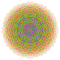 |
 |
 |
 |
 |
 |
 |
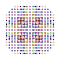 |
t0,1,4,5,7{3,3,3,3,3,3,4} Heptipentisteritruncated 8-orthoplex Exitericellitruncated diacosipentacontahexazetton |
||
| 194 |  |
 |
 |
 |
 |
 |
 |
 |
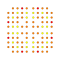
t0,2,3,5,7{4,3,3,3,3,3,3} Heptipentiruncicantellated 8-cube Exiteriprismatorhombated octeract |
||
| 195 | 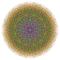 |
 |
 |
 |
 |
 |
 |
 |
t0,2,3,5,6{4,3,3,3,3,3,3} Hexipentiruncicantellated 8-cube Petiteriprismatorhombated octeract |
||
| 196 |  |
 |
 |
 |
 |
 |
 |
 |
t0,2,3,4,7{4,3,3,3,3,3,3} Heptisteriruncicantellated 8-cube Exicelliprismatorhombated octeract |
||
| 197 |  |
 |
 |
 |
 |
 |
 |
 |
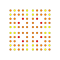
t0,2,3,4,6{4,3,3,3,3,3,3} Hexisteriruncicantellated 8-cube Peticelliprismatorhombated octeract |
||
| 198 |  |
 |
 |
 |
 |
 |
 |
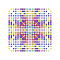 |
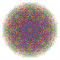
t0,2,3,4,5{4,3,3,3,3,3,3} Pentisteriruncicantellated 8-cube Tericelliprismatorhombated octeract |
||
| 199 |  |
 |
 |
 |
 |
 |
 |
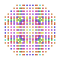 |
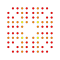
t0,1,2,6,7{3,3,3,3,3,3,4} Heptihexicantitruncated 8-orthoplex Exipetigreatorhombated diacosipentacontahexazetton |
||
| 200 |  |
 |
 |
 |
 |
 |
 |
 |
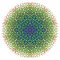
t0,1,3,6,7{3,3,3,3,3,3,4} Heptihexiruncitruncated 8-orthoplex Exipetiprismatotruncated diacosipentacontahexazetton |
||
| 201 | 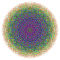 |
 |
 |
 |
 |
 |
 |
 |
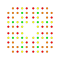
t0,1,4,5,7{4,3,3,3,3,3,3} Heptipentisteritruncated 8-cube Exitericellitruncated octeract |
||
| 202 |  |
 |
 |
 |
 |
 |
 |
 |
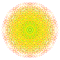
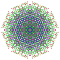
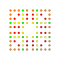
t0,1,4,5,6{4,3,3,3,3,3,3} Hexipentisteritruncated 8-cube Petitericellitruncated octeract |
||
| 203 | 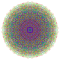 |
 |
 |
 |
 |
 |
 |
 |
t0,1,3,6,7{4,3,3,3,3,3,3} Heptihexiruncitruncated 8-cube Exipetiprismatotruncated octeract |
||
| 204 |  |
 |
 |
 |
 |
 |
 |
 |
t0,1,3,5,7{4,3,3,3,3,3,3} Heptipentiruncitruncated 8-cube Exiteriprismatotruncated octeract |
||
| 205 |  |
 |
 |
 |
 |
 |
 |
 |
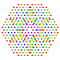
t0,1,3,5,6{4,3,3,3,3,3,3} Hexipentiruncitruncated 8-cube Petiteriprismatotruncated octeract |
||
| 206 |  |
 |
 |
 |
 |
 |
 |
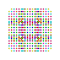 |
t0,1,3,4,7{4,3,3,3,3,3,3} Heptisteriruncitruncated 8-cube Exicelliprismatotruncated octeract |
||
| 207 |  |
 |
 |
 |
 |
 |
 |
 |
t0,1,3,4,6{4,3,3,3,3,3,3} Hexisteriruncitruncated 8-cube Peticelliprismatotruncated octeract |
||
| 208 |  |
 |
 |
 |
 |
 |
 |
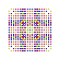 |
t0,1,3,4,5{4,3,3,3,3,3,3} Pentisteriruncitruncated 8-cube Tericelliprismatotruncated octeract |
||
| 209 |  |
 |
 |
 |
 |
 |
 |
 |
t0,1,2,6,7{4,3,3,3,3,3,3} Heptihexicantitruncated 8-cube Exipetigreatorhombated octeract |
||
| 210 |  |
 |
 |
 |
 |
 |
 |
 |
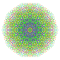
t0,1,2,5,7{4,3,3,3,3,3,3} Heptipenticantitruncated 8-cube Exiterigreatorhombated octeract |
||
| 211 |  |
 |
 |
 |
 |
 |
 |
 |
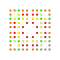
t0,1,2,5,6{4,3,3,3,3,3,3} Hexipenticantitruncated 8-cube Petiterigreatorhombated octeract |
||
| 212 |  |
 |
 |
 |
 |
 |
 |
 |
t0,1,2,4,7{4,3,3,3,3,3,3} Heptistericantitruncated 8-cube Exicelligreatorhombated octeract |
||
| 213 |  |
 |
 |
 |
 |
 |
 |
 |
t0,1,2,4,6{4,3,3,3,3,3,3} Hexistericantitruncated 8-cube Peticelligreatorhombated octeract |
||
| 214 |  |
 |
 |
 |
 |
 |
 |
 |
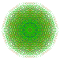
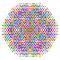
t0,1,2,4,5{4,3,3,3,3,3,3} Pentistericantitruncated 8-cube Tericelligreatorhombated octeract |
||
| 215 |  |
 |
 |
 |
 |
 |
 |
 |
t0,1,2,3,7{4,3,3,3,3,3,3} Heptiruncicantitruncated 8-cube Exigreatoprismated octeract |
||
| 216 | 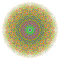 |
 |
 |
 |
 |
 |
 |
 |
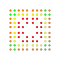
t0,1,2,3,6{4,3,3,3,3,3,3} Hexiruncicantitruncated 8-cube Petigreatoprismated octeract |
||
| 217 |  |
 |
 |
 |
 |
 |
 |
 |
t0,1,2,3,5{4,3,3,3,3,3,3} Pentiruncicantitruncated 8-cube Terigreatoprismated octeract |
||
| 218 |  |
 |
 |
 |
 |
 |
 |
 |
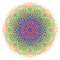
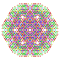
t0,1,2,3,4{4,3,3,3,3,3,3} Steriruncicantitruncated 8-cube Great cellated octeract |
||
| 219 | 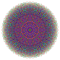 |
 |
 |
 |
 |
 |
 |
 |
t0,1,2,3,4,5{3,3,3,3,3,3,4} Pentisteriruncicantitruncated 8-orthoplex Great terated diacosipentacontahexazetton |
||
| 220 | 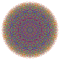 |
 |
 |
 |
 |
 |
 |
 |
t0,1,2,3,4,6{3,3,3,3,3,3,4} Hexisteriruncicantitruncated 8-orthoplex Petigreatocellated diacosipentacontahexazetton |
||
| 221 |  |
 |
 |
 |
 |
 |
 |
 |
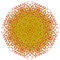
t0,1,2,3,5,6{3,3,3,3,3,3,4} Hexipentiruncicantitruncated 8-orthoplex Petiterigreatoprismated diacosipentacontahexazetton |
||
| 222 |  |
 |
 |
 |
 |
 |
 |
 |
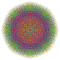
t0,1,2,4,5,6{3,3,3,3,3,3,4} Hexipentistericantitruncated 8-orthoplex Petitericelligreatorhombated diacosipentacontahexazetton |
||
| 223 |  |
 |
 |
 |
 |
 |
 |
 |
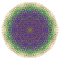
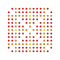
t0,1,3,4,5,6{3,3,3,3,3,3,4} Hexipentisteriruncitruncated 8-orthoplex Petitericelliprismatotruncated diacosipentacontahexazetton |
||
| 224 |  |
 |
 |
 |
 |
 |
 |
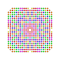 |
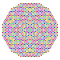
t0,2,3,4,5,6{3,3,3,3,3,3,4} Hexipentisteriruncicantellated 8-orthoplex Petitericelliprismatorhombated diacosipentacontahexazetton |
||
| 225 |  |
 |
 |
 |
 |
 |
 |
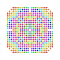 |
t1,2,3,4,5,6{4,3,3,3,3,3,3} Bipentisteriruncicantitruncated 8-cube Great biteri-octeractidiacosipentacontahexazetton |
||
| 226 |  |
 |
 |
 |
 |
 |
 |
 |
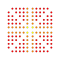
t0,1,2,3,4,7{3,3,3,3,3,3,4} Heptisteriruncicantitruncated 8-orthoplex Exigreatocellated diacosipentacontahexazetton |
||
| 227 |  |
 |
 |
 |
 |
 |
 |
 |
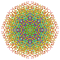
t0,1,2,3,5,7{3,3,3,3,3,3,4} Heptipentiruncicantitruncated 8-orthoplex Exiterigreatoprismated diacosipentacontahexazetton |
||
| 228 |  |
 |
 |
 |
 |
 |
 |
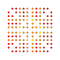
t0,1,2,4,5,7{3,3,3,3,3,3,4} Heptipentistericantitruncated 8-orthoplex Exitericelligreatorhombated diacosipentacontahexazetton |
|||
| 229 |  |
 |
 |
 |
 |
 |
 |
t0,1,3,4,5,7{3,3,3,3,3,3,4} Heptipentisteriruncitruncated 8-orthoplex Exitericelliprismatotruncated diacosipentacontahexazetton |
|||
| 230 | 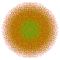 |
 |
 |
 |
 |
 |
 |
t0,2,3,4,5,7{4,3,3,3,3,3,3} Heptipentisteriruncicantellated 8-cube Exitericelliprismatorhombi-octeractidiacosipentacontahexazetton |
|||
| 231 | 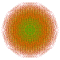 |
 |
 |
 |
 |
 |
 |
t0,2,3,4,5,6{4,3,3,3,3,3,3} Hexipentisteriruncicantellated 8-cube Petitericelliprismatorhombated octeract |
|||
| 232 | 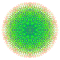 |
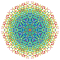 |
 |
 |
 |
 |
 |
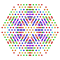
t0,1,2,3,6,7{3,3,3,3,3,3,4} Heptihexiruncicantitruncated 8-orthoplex Exipetigreatoprismated diacosipentacontahexazetton |
|||
| 233 | 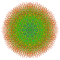 |
 |
 |
 |
 |
 |
 |
t0,1,2,4,6,7{3,3,3,3,3,3,4} Heptihexistericantitruncated 8-orthoplex Exipeticelligreatorhombated diacosipentacontahexazetton |
|||
| 234 |  |
 |
 |
 |
 |
 |
 |
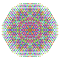
t0,1,3,4,6,7{4,3,3,3,3,3,3} Heptihexisteriruncitruncated 8-cube Exipeticelliprismatotrunki-octeractidiacosipentacontahexazetton |
|||
| 235 |  |
 |
 |
 |
 |
 |
 |
t0,1,3,4,5,7{4,3,3,3,3,3,3} Heptipentisteriruncitruncated 8-cube Exitericelliprismatotruncated octeract |
|||
| 236 |  |
 |
 |
 |
 |
 |
 |
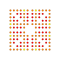
t0,1,3,4,5,6{4,3,3,3,3,3,3} Hexipentisteriruncitruncated 8-cube Petitericelliprismatotruncated octeract |
|||
| 237 |  |
 |
 |
 |
 |
 |
 |
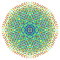
t0,1,2,5,6,7{4,3,3,3,3,3,3} Heptihexipenticantitruncated 8-cube Exipetiterigreatorhombi-octeractidiacosipentacontahexazetton |
|||
| 238 |  |
 |
 |
 |
 |
 |
 |
t0,1,2,4,6,7{4,3,3,3,3,3,3} Heptihexistericantitruncated 8-cube Exipeticelligreatorhombated octeract |
|||
| 239 |  |
 |
 |
 |
 |
 |
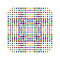 |
t0,1,2,4,5,7{4,3,3,3,3,3,3} Heptipentistericantitruncated 8-cube Exitericelligreatorhombated octeract |
|||
| 240 |  |
 |
 |
 |
 |
 |
 |
t0,1,2,4,5,6{4,3,3,3,3,3,3} Hexipentistericantitruncated 8-cube Petitericelligreatorhombated octeract |
|||
| 241 | 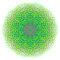 |
 |
 |
 |
 |
 |
 |
t0,1,2,3,6,7{4,3,3,3,3,3,3} Heptihexiruncicantitruncated 8-cube Exipetigreatoprismated octeract |
|||
| 242 |  |
 |
 |
 |
 |
 |
 |
t0,1,2,3,5,7{4,3,3,3,3,3,3} Heptipentiruncicantitruncated 8-cube Exiterigreatoprismated octeract |
|||
| 243 |  |
 |
 |
 |
 |
 |
 |
t0,1,2,3,5,6{4,3,3,3,3,3,3} Hexipentiruncicantitruncated 8-cube Petiterigreatoprismated octeract |
|||
| 244 |  |
 |
 |
 |
 |
 |
 |
t0,1,2,3,4,7{4,3,3,3,3,3,3} Heptisteriruncicantitruncated 8-cube Exigreatocellated octeract |
|||
| 245 | 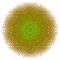 |
 |
 |
 |
 |
 |
 |
t0,1,2,3,4,6{4,3,3,3,3,3,3} Hexisteriruncicantitruncated 8-cube Petigreatocellated octeract |
|||
| 246 |  |
 |
 |
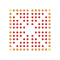 |
 |
 |
 |
t0,1,2,3,4,5{4,3,3,3,3,3,3} Pentisteriruncicantitruncated 8-cube Great terated octeract |
|||
| 247 |  |
 |
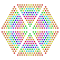 |
 |
 |
 |
 |
t0,1,2,3,4,5,6{3,3,3,3,3,3,4} Hexipentisteriruncicantitruncated 8-orthoplex Great petated diacosipentacontahexazetton |
|||
| 248 | 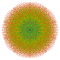 |
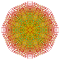 |
 |
 |
 |
 |
 |
t0,1,2,3,4,5,7{3,3,3,3,3,3,4} Heptipentisteriruncicantitruncated 8-orthoplex Exigreatoterated diacosipentacontahexazetton |
|||
| 249 |  |
 |
 |
 |
 |
 |
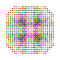 |
t0,1,2,3,4,6,7{3,3,3,3,3,3,4} Heptihexisteriruncicantitruncated 8-orthoplex Exipetigreatocellated diacosipentacontahexazetton |
|||
| 250 |  |
 |
 |
 |
 |
 |
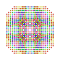 |
t0,1,2,3,5,6,7{3,3,3,3,3,3,4} Heptihexipentiruncicantitruncated 8-orthoplex Exipetiterigreatoprismated diacosipentacontahexazetton |
|||
| 251 |  |
 |
 |
 |
 |
 |
 |
t0,1,2,3,5,6,7{4,3,3,3,3,3,3} Heptihexipentiruncicantitruncated 8-cube Exipetiterigreatoprismated octeract |
|||
| 252 |  |
 |
 |
 |
 |
 |
 |
t0,1,2,3,4,6,7{4,3,3,3,3,3,3} Heptihexisteriruncicantitruncated 8-cube Exipetigreatocellated octeract |
|||
| 253 |  |
 |
 |
 |
 |
 |
 |
t0,1,2,3,4,5,7{4,3,3,3,3,3,3} Heptipentisteriruncicantitruncated 8-cube Exigreatoterated octeract |
|||
| 254 |  |
 |
 |
 |
 |
 |
 |
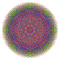
t0,1,2,3,4,5,6{4,3,3,3,3,3,3} Hexipentisteriruncicantitruncated 8-cube Great petated octeract |
|||
| 255 |  |
 |
 |
 |
 |
 |
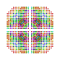 |
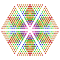
t0,1,2,3,4,5,6,7{4,3,3,3,3,3,3} Omnitruncated 8-cube Great exi-octeractidiacosipentacontahexazetton |
|||
| 256 |  |
 |
 |
 |
 |
 |
 |
 |
 |
 |
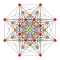
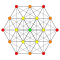
h0{4,3,3,3,3,3,3} 8-demicube Hemiocteract |
References
Klitzing, Richard. "8D uniform polytopes (polyzetta)".
Notes
|
Fundamental convex regular and uniform polytopes in dimensions 2–10
|
||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Family | An | Bn | I2(p) / Dn | E6 / E7 / E8 / F4 / G2 | Hn | |||||||
| Regular polygon | Triangle | Square | p-gon | Hexagon | Pentagon | |||||||
| Uniform polyhedron | Tetrahedron | Octahedron • Cube | Demicube | Dodecahedron • Icosahedron | ||||||||
| Uniform 4-polytope | 5-cell | 16-cell • Tesseract | Demitesseract | 24-cell | 120-cell • 600-cell | |||||||
| Uniform 5-polytope | 5-simplex | 5-orthoplex • 5-cube | 5-demicube | |||||||||
| Uniform 6-polytope | 6-simplex | 6-orthoplex • 6-cube | 6-demicube | 122 • 221 | ||||||||
| Uniform 7-polytope | 7-simplex | 7-orthoplex • 7-cube | 7-demicube | 132 • 231 • 321 | ||||||||
| Uniform 8-polytope | 8-simplex | 8-orthoplex • 8-cube | 8-demicube | 142 • 241 • 421 | ||||||||
| Uniform 9-polytope | 9-simplex | 9-orthoplex • 9-cube | 9-demicube | |||||||||
| Uniform 10-polytope | 10-simplex | 10-orthoplex • 10-cube | 10-demicube | |||||||||
| Uniform n-polytope | n-simplex | n-orthoplex • n-cube | n-demicube | 1k2 • 2k1 • k21 | n-pentagonal polytope | |||||||
| Topics: Polytope families • Regular polytope • List of regular polytopes and compounds | ||||||||||||
Undergraduate Texts in Mathematics
Graduate Studies in Mathematics
Hellenica World - Scientific Library
Retrieved from "http://en.wikipedia.org/"
All text is available under the terms of the GNU Free Documentation License

