Archimedes' quadruplets

In geometry, Archimedes' quadruplets are four congruent circles associated with an arbelos. Introduced by Frank Power in the summer of 1998, each have the same area as Archimedes' twin circles, making them Archimedean circles.[1][2][3]

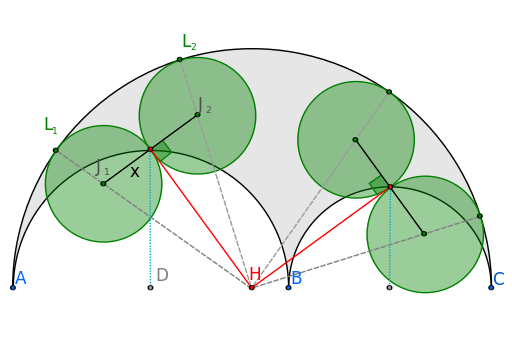
Each of the Archimedes' quadruplets (green) have equal area to each other and to Archimedes' twin circles

Construction

An arbelos is formed from three collinear points A, B, and C, by the three semicircles with diameters AB, AC, and BC. Let the two smaller circles have radii r1 and r2, from which it follows that the larger semicircle has radius r = r1+r2. Let the points D and E be the center and midpoint, respectively, of the semicircle with the radius r1. Let H be the midpoint of line AC. Then two of the four quadruplet circles are tangent to line HE at the point E, and are also tangent to the outer semicircle. The other two quadruplet circles are formed in a symmetric way from the semicircle with radius r2.
Proof of congruency

According to Proposition 5 of Archimedes' Book of Lemmas, the common radius of Archimedes' twin circles is:

\( \frac{r_1\cdot r_2}{r}. \)

By the Pythagorean theorem:

\( \left(HE\right)^2=\left(r_1\right)^2+\left(r_2\right)^2. \)

Then, create two circles with centers Ji perpendicular to HE, tangent to the large semicircle at point Li, tangent to point E, and with equal radii x. Using the Pythagorean theorem:

\( \left(HJ_i\right)^2=\left(HE\right)^2+x^2=\left(r_1\right)^2+\left(r_2\right)^2+x^2 \)

Also:

\( HJ_i=HL_i-x=r-x=r_1+r_2-x~ \)

Combining these gives:

\( \left(r_1\right)^2+\left(r_2\right)^2+x^2=\left(r_1+r_2-x\right)^2 \)

Expanding, collecting to one side, and factoring:

\( 2r_1r_2-2x\left(r_1+r_2\right)=0 \)

Solving for x:

\( x=\frac{r_1\cdot r_2}{r_1+r_2}=\frac{r_1\cdot r_2}{r} \)

Proving that each of the Archimedes' quadruplets' areas is equal to each of Archimedes' twin circles' areas.[4]
References

Power, Frank (2005), "Some More Archimedean Circles in the Arbelos", in Yiu, Paul (ed.), Forum Geometricorum, 5 (published 2005-11-02), pp. 133–134, ISSN 1534-1178, retrieved 2008-04-13
Online catalogue of Archimedean circles
Clayton W. Dodge, Thomas Schoch, Peter Y. Woo, Paul Yiu (1999). "Those Ubiquitous Archimedean Circles". PDF.

Bogomolny, Alexander. "Archimedes' Quadruplets". Archived from the original on 12 May 2008. Retrieved 2008-04-13.