.
Στην επιστήμη των υπολογιστών, ένα δυαδικό δέντρο είναι μια δενδρική Δομή δεδομένων στην οποία κάθε κόμβος έχει το πολύ δύο παιδιά, που αναφέρονται ως το αριστερό παιδί και το δεξιό παιδί . Ένας αναδρομικός ορισμός με την χρήση Θεωρίας Συνόλων είναι ότι δυαδικό δένδρο (μη κενό) είναι μια πλειάδα ( L, S, R ), όπου τα L και R είναι δυαδικά δέντρα ή το κενό σύνολο και το S είναι ένα μοναδιαίο σύνολο(singleton) .[1] Ορισμένοι συγγραφείς επιτρέπουν στο δυαδικό δέντρο να είναι και το κενό σύνολο.[2]
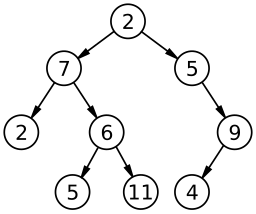
Ένα δυαδικό δέντρο με μέγεθος 9 και ύψος 3 επιπέδων, με έναν ριζικό κόμβο του οποίου η τιμή είναι 2. Το παραπάνω δέντρο δεν είναι ισορροπημένο και δεν έχει ταξινομηθεί.
Από την άποψη της θεωρίας γραφημάτων, τα δυαδικά (και τα Κ-οστά) δέντρα, όπως ορίζονται εδώ, είναι στην πραγματικότητα δενδρικά γραφήματα .[3] Ένα δυαδικό δέντρο μπορεί έτσι να ονομάζεται επίσης διαιρετικό γράφημα - ένας όρος που εμφανίζεται σε κάποια πολύ παλιά βιβλία προγραμματισμού,[4] πριν επικρατήσει η σύγχρονη ορολογία της πληροφορικής. Είναι επίσης δυνατή η ερμηνεία ενός δυαδικού δέντρου ως μη κατευθυνόμενου, αντί κατευθυνόμενου γραφήματος, οπότε ένα δυαδικό δέντρο είναι ένα δέντρο που έχει ταξινομηθεί και έχει ρίζα .[5] Ορισμένοι συγγραφείς χρησιμοποιούν τον όρο δυαδικό δέντρο με ρίζα αντί για δυαδικό δέντρο για να τονίσουν το γεγονός ότι το δέντρο έχει ρίζες, αλλά όπως ορίστηκε παραπάνω, ένα δυαδικό δέντρο είναι πάντα ριζωμένο.[6] Ένα δυαδικό δέντρο είναι μια ειδική περίπτωση ενός διατεταγμένου Κ-οστού δέντρου, όπου το κ είναι 2.
Στα μαθηματικά, το τί ονομάζεται δυαδικό δέντρο μπορεί να διαφέρει σημαντικά, ανάλογα με τον συγγραφέα. Κάποιοι χρησιμοποιούν τον ορισμό που χρησιμοποιείται συνήθως στην επιστήμη των υπολογιστών ,αλλά άλλοι το ορίζουν ως κάθε μη-φύλλο με ακριβώς δύο παιδιά και χωρίς απαραίτητα αυτά να έχουν καθορισμένη σειρά.[7]
Στην επιστήμη των υπολογιστών, τα δυαδικά δέντρα χρησιμοποιούνται με δύο πολύ διαφορετικούς τρόπους:
Πρώτον, ως μέσο πρόσβασης σε κόμβους με βάση κάποια τιμή ή όνομα που ειναι συνδεδεμένο με κάθε κόμβο.[8] Τα δυαδικά δέντρα που έχουν επισημανθεί με αυτόν τον τρόπο χρησιμοποιούνται για την υλοποίηση δυαδικών δέντρων αναζήτησης και δυαδικών σωρών, και χρησιμοποιούνται για αποδοτική αναζήτηση και ταξινόμηση . Ο ορισμός των κόμβων(εκτός της ρίζας) ως "αριστερό" ή "δεξιό" παιδί (ακόμα και όταν υπάρχει μόνο ένα παιδί), έχει απτή σημασία σε ορισμένες από αυτές τις εφαρμογές, και πιο συγκεκριμένα είναι σημαντικό σε δυαδικά δέντρα αναζήτησης.[9] Ωστόσο, η θέση και διάταξη των εν λόγω κόμβων στο δέντρο δεν έχει να κάνει με τα θεωρήματα αυτα καθεαυτό. Για παράδειγμα, σε ένα συνηθισμένο δυαδικό δένδρο αναζήτησης, η τοποθέτηση των κόμβων εξαρτάται σχεδόν εξ ολοκλήρου από τη σειρά με την οποία προστέθηκαν στο δένδρο και μπορεί να υποστεί αλλαγές (για παράδειγμα με εξισορρόπηση ) χωρίς να αλλάξει η ερμηνεία του δένδρου.
Δεύτερον, ως αναπαράσταση δεδομένων με μια σχετική διχαστική δομή. Σε τέτοιες περιπτώσεις, η συγκεκριμένη διάταξη των κόμβων κάτω ή / και αριστερά ή δεξιά των άλλων κόμβων είναι μέρος της πληροφορίας (δηλαδή, η αλλαγή θα άλλαζε την ερμηνεία). Παραδείγματα αυτού του τύπου είναι η κωδικοποίηση Huffman και τα κλαδογράμματα . Η καθημερινή διαχώριση ενός εγγράφου σε κεφάλαια, τμήματα, παραγράφους και τα λοιπά είναι ένα ανάλογο παράδειγμα με κ-οστά και όχι με δυαδικά δέντρα.
Ορισμοί
Αναδρομικός ορισμός
Για να ορίσουμε πραγματικά ένα δυαδικό δέντρο σε γενικές γραμμές, πρέπει να επιτρέψουμε την πιθανότητα μόνο ένα από τα παιδιά να είναι άδειο. Ένα τεχνούργημα, το οποίο σε ορισμένα εγχειρίδια ονομάζεται εκτεταμένο δυαδικό δένδρο είναι απαραίτητο για το σκοπό αυτό. Επομένως, ένα εκτεταμένο δυαδικό δένδρο ορίζεται αναδρομικά ως:[10]
το κενό σύνολο είναι ένα εκτεταμένο δυαδικό δέντρο
εάν το Τ 1 και Τ 2 είναι εκτεταμένα δυαδικά δένδρα, τότε ωςT 1 • Τ 2 συμβολίζεται το εκτεταμένο δυαδικό δένδρο που λαμβάνεται με την προσθήκη μιας ρίζας r, συνδεδεμένοή προς τα αριστερά στο Τ 1 και προς τα δεξιά στο Τ 2 ,με την προσθήκη ακμών όταν αυτά υποδέντρα είναι μή κενά.
Ένας άλλος τρόπος να φανταστούμε αυτή την κατασκευή (και να κατανοήσουμε την ορολογία) είναι να εξετάσουμε αντί για το άδειο σύνολο ένα διαφορετικό τύπο κόμβου - για παράδειγμα τετράγωνους κόμβους εάν οι κανονικοί είναι κύκλοι.[11]
Χρήση εννοιών θεωρίας γραφημάτων
Ένα δυαδικό δέντρο είναι ένα δένδρο με ρίζα,το οποίο είναι επίσης διατεταγμένο δέντρο (ή αλλιώς επίπεδο δένδρο), στο οποίο κάθε κόμβος έχει το πολύ δύο παιδιά. Ένα ριζωμένο δέντρο από την φύση του προσδίδει μια έννοια των επιπέδων (απόσταση από τη ρίζα), έτσι για κάθε κόμβο μια έννοια των παιδιών μπορεί να οριστεί ως οι κόμβοι που συνδέονται με αυτό ένα επίπεδο προς τα κάτω. Η σειρά αυτών των παιδιών (π.χ., σχεδιάζοντας τα σε ένα επίπεδο) καθιστά δυνατή τη διάκριση του αριστερού παιδιού από το δεξιό παιδί.[12] Αλλά αυτό από μόνο του δεν είναι αρκέτο για να γίνει διάκριση μεταξύ ενός κόμβου με αριστερό, αλλά όχι δεξιό παιδί από έναν με δεξιό αλλά χωρίς αριστερό παιδί.
Η απαραίτητη διάκριση μπορεί να γίνει διαχωρίζοντας πρώτα τις άκρες, δηλ. ορίζοντας το δυαδικό δέντρο ως τριπλέτα (V, E 1, E 2 ), όπου (V, E 1 ∪ E 2 ) είναι ένα δένδρο με ρίζες, το E 1 ∩ E 2 είναι κενό και επίσης για κάθε j ∈ {1, 2} κάθε κόμβος έχει το πολύ ένα παιδί E j .[13] Ένας πιο άτυπος τρόπος για να κάνουμε τη διάκριση είναι να πούμε, επικαλλούμενοι την Εγκυκλοπαίδεια των Μαθηματικών, ότι "κάθε κόμβος έχει ένα αριστερό παιδί, ένα δεξιό παιδί, κανένα εξ αυτών ή και τα δύο" και να διευκρινίσουμε ότι αυτά "είναι όλα διαφορετικά" δυαδικά δέντρα.
Τύποι δυαδικών δέντρων
Η ορολογία των δένδρων δεν είναι καλά τυποποιημένη και έτσι ποικίλλει στη βιβλιογραφία.
Ένα δυαδικό δέντρο με ρίζα έχει μία ρίζα και κάθε κόμβος έχει το πολύ δύο παιδιά.
Ένα πλήρες δυαδικό δέντρο
Ένα διάγραμμα των προγόνων που αντιστοιχεί σε ένα τέλειο δυαδικό δένδρο με βάθος 4.
Ένα πλήρες δυαδικό δέντρο (μερικές φορές αναφέρεται ως ένα σωστό [14] ή επίπεδο δυαδικό δέντρο) [15][16] είναι ένα δέντρο στο οποίο κάθε κόμβος έχει 0 ή 2 παιδιά. Ένας άλλος τρόπος ορισμού ενός πλήρους δυαδικού δέντρου είναι ένας αναδρομικός ορισμός . Ένα πλήρες δυαδικό δέντρο είναι είτε:[10]
Μια μοναδική κορυφή.
Ένα δέντρο του οποίου ο κόμβος ρίζας έχει δύο υποδέντρα, και τα δύο εκ των οποίων είναι πλήρη δυαδικά δέντρα.
Σε ένα συμπληρωμένο δυαδικό δέντρο κάθε επίπεδο, εκτός ίσως από το τελευταίο, είναι εντελώς γεμάτο και όλοι οι κόμβοι στο τελευταίο επίπεδο είναι τοποθετημένοι όσο το δυνατόν πιο αριστερά. Μπορεί να έχει μεταξύ 1 και 2 h κόμβους στο τελευταίο επίπεδο h .[17] Ένας εναλλακτικός ορισμός είναι ένα τέλειο δέντρο του οποίου τα δεξιά φύλλα (ίσως όλα) έχουν αφαιρεθεί. Ορισμένοι συγγραφείς χρησιμοποιούν τον όρο πλήρες για να αναφερθούν σε ένα τέλειο δυαδικό δέντρο όπως ορίζεται παρακάτω, οπότε καλούν αυτό το είδος δέντρου (με ένα πιθανώς μη συμπληρωμένο τελευταίο επίπεδο) ένα σχεδόν πλήρες δυαδικό δέντρο ή ως επί το πλείστον πλήρες δυαδικό δέντρο.[18][19] Ένα πλήρες δυαδικό δέντρο μπορεί να αναπαρασταθεί αποδοτικά με την χρήση ενός πίνακα.
Ένα συμπληρωμένο δυαδικό δέντρο (που δεν είναι πλήρες)
Ένα τέλειο δυαδικό δέντρο είναι ένα δυαδικό δέντρο στο οποίο όλοι οι εσωτερικοί κόμβοι έχουν δύο παιδιά και όλα τα φύλλα έχουν το ίδιο βάθος (ή το ίδιο επίπεδο).[20] Ένα παράδειγμα ενός τέλειου δυαδικού δένδρου είναι το (μη αιμομικτικό) γράφημα των προγόνων ενός ατόμου σε ένα μέχρι ένα δεδομένο βάθος, καθώς κάθε άτομο έχει ακριβώς δύο βιολογικούς γονείς (μία μητέρα και έναν πατέρα). Με την προϋπόθεση ότι ο πίνακας των προγόνων εμφανίζει πάντα τη μητέρα και τον πατέρα στην ίδια πλευρά για έναν δεδομένο κόμβο, το φύλο τους μπορεί να θεωρηθεί ως αναλογία αριστερού και δεξιού παιδιού, με την χρήση του όρου "παιδιά" ως όρος στην θεωρία γραφημάτων. Επομένως, ένα τέλειο δέντρο είναι πάντα συμπληρωμένο, αλλά ένα συμπληρωμένο δέντρο δεν είναι απαραιτήτως τέλειο.
Στο άπειρο συμπληρωμένο δυαδικό δέντρο, κάθε κόμβος έχει δύο παιδιά (και έτσι το σύνολο των επιπέδων είναι αριθμήσιμο και άπειρο ). Το σύνολο όλων των κόμβων είναι αριθμήσιμο και άπειρο, αλλά το σύνολο όλων των άπειρων(σε μήκος) μονοπατιών που ξεκινούν από τη ρίζα είναι μη αριθμήσιμο, έχοντας την πληθικότητα του συνεχούς . Αυτές οι διαδρομές αντιστοιχούν σε μια αμφιμονοσήμαντη (1-προς-1) ένωση που διατηρεί την σείρα των κόμβων με τα σημεία του σετ Cantor ή (χρησιμοποιώντας το παράδειγμα ενός δέντρου Stern-Brocot ) με το σύνολο θετικών άρρητων αριθμών .
Ένα ισορροπημένο δυαδικό δέντρο είναι μια δομή δυαδικού δέντρου στην οποία το αριστερό και το δεξιό υποδέντρο κάθε κόμβου διαφέρουν σε ύψος όχι περισσότερο από 1.[21] Μπορεί κανείς επίσης να θεωρήσει ως τέτοια δυαδικά δέντρα στα οποία κανένα φύλλο δεν απέχει πολύ περισσότερο από τη ρίζα, από οποιοδήποτε άλλο φύλλο. (Τα διαφορετικά συστήματα εξισορρόπησης επιτρέπουν διαφορετικούς ορισμούς του "πολύ περισσότερο".[22] )
Ένα εκφυλισμένο δέντρο είναι ένα δέντρο στο οποίο κάθε γονικός κόμβος έχει μόνο ένα παιδί.[23] Αυτό σημαίνει ότι το συγκεκριμένο δέντρο είναι μια συνδεδεμένη λίστα.
Ιδιότητες δυαδικών δέντρων
Ο αριθμός κόμβων n n σε ένα πλήρες δυαδικό δέντρο, είναι τουλάχιστον \( {\displaystyle n=2h+1 \) } και το πολύ \( {\displaystyle n=2^{h+1}-1}, \) που h είναι το ύψος του δέντρου. Ένα δέντρο που αποτελείται μόνο από έναν κόμβο ρίζας έχει ύψος 0.
Ο αριθμός των φύλλων l σε ένα τέλειο δυαδικό δέντρο, είναι \( {\displaystyle l=(n+1)/2} \) επειδή ο αριθμός των μη φύλλων (γνωστός και ως εσωτερικοί) κόμβων \( {\displaystyle n-l=\sum _{k=0}^{\log _{2}(l)-1}2^{k}=2^{\log _{2}(l)}-1=l-1} \).
Αυτό σημαίνει ότι ένα πλήρες δυαδικό δέντρο με l φύλλα έχει \( {\displaystyle n=2l-1} \)κόμβους.
Σε ένα ισορροπημένο πλήρες δυαδικό δέντρο, \( {\displaystyle h=\lceil \log _{2}(l)\rceil +1=\lceil \log _{2}((n+1)/2)\rceil +1=\lceil \log _{2}(n+1)\rceil }. \)
Σε ένα τέλειο δυαδικό δέντρο, \( {\displaystyle l=2^{h}} \), έτσι \( {\displaystyle n=2^{h+1}-1} . \)
Ο μέγιστος δυνατός αριθμός μηδενικών συνδέσεων (δηλαδή απουσιάζοντα παιδιά κόμβων) σε ένα συμπληρωμένο δυαδικό δέντρο n κόμβων είναι ( n +1), όπου μόνο 1 κόμβος υπάρχει στο κατώτατο επίπεδο προς τα αριστερά. Το ίδιο ισχύει για κάθε δυαδικό δέντρο.
Ο αριθμός των εσωτερικών κόμβων σε ένα πλήρες δυαδικό δέντρο των n κόμβων είναι \( {\displaystyle \lfloor n/2\rfloor } . \)
Για κάθε μη κενό δυαδικό δένδρο με n 0 φύλλα και n 2 κόμβους με βαθμό 2, n 0 = n 2 + 1.[24]
Βιβλιογραφικές αναφορές
Αναφορές
Rowan Garnier· John Taylor (2009). Discrete Mathematics: Proofs, Structures and Applications, Third Edition. CRC Press. σελ. 620. ISBN 978-1-4398-1280-8.
Steven S Skiena (2009). The Algorithm Design Manual. Springer Science & Business Media. σελ. 77. ISBN 978-1-84800-070-4.
Knuth (1997). The Art Of Computer Programming, Volume 1, 3/E. Pearson Education. σελ. 363. ISBN 0-201-89683-4.
Iván Flores (1971). Computer programming system/360. Prentice-Hall. σελ. 39.
Kenneth Rosen (2011). Discrete Mathematics and Its Applications, 7th edition. McGraw-Hill Science. σελ. 749. ISBN 978-0-07-338309-5.
David R. Mazur (2010). Combinatorics: A Guided Tour. Mathematical Association of America. σελ. 246. ISBN 978-0-88385-762-5.
L.R. Foulds (1992). Graph Theory Applications. Springer Science & Business Media. σελ. 32. ISBN 978-0-387-97599-3.
David Makinson (2009). Sets, Logic and Maths for Computing. Springer Science & Business Media. σελ. 199. ISBN 978-1-84628-845-6.
Jonathan L. Gross (2007). Combinatorial Methods with Computer Applications. CRC Press. σελ. 248. ISBN 978-1-58488-743-0.
Kenneth Rosen (2011). Discrete Mathematics and Its Applications 7th edition. McGraw-Hill Science. σελίδες 352–353. ISBN 978-0-07-338309-5.
Te Chiang Hu· Man-tak Shing (2002). Combinatorial Algorithms. Courier Dover Publications. σελ. 162. ISBN 978-0-486-41962-6.
Lih-Hsing Hsu· Cheng-Kuan Lin (2008). Graph Theory and Interconnection Networks. CRC Press. σελ. 66. ISBN 978-1-4200-4482-9.
J. Flum· M. Grohe (2006). Parameterized Complexity Theory. Springer. σελ. 245. ISBN 978-3-540-29953-0.
Tamassia, Michael T. Goodrich, Roberto (2011). Algorithm design : foundations, analysis, and Internet examples (2 έκδοση). New Delhi: Wiley-India. σελ. 76. ISBN 978-81-265-0986-7.
«full binary tree». NIST.
Richard Stanley, Enumerative Combinatorics, volume 2, p.36
«complete binary tree». NIST.
«almost complete binary tree». Αρχειοθετήθηκε από το πρωτότυπο στις 4 Μαρτίου 2016. Ανακτήθηκε στις 30 Ιανουαρίου 2020.
«nearly complete binary tree» (PDF).
«perfect binary tree». NIST.
Aaron M. Tenenbaum, et al. Data Structures Using C, Prentice Hall, 1990 (ISBN 0-13-199746-7)
Paul E. Black (ed.), entry for data structure in Dictionary of Algorithms and Data Structures. U.S. National Institute of Standards and Technology. 15 December 2004. Online version Σφάλμα στο πρότυπο webarchive: Ελέγξτε την τιμή |url=. Empty. Accessed 2010-12-19.
Parmar, Anand K. (22 Ιανουαρίου 2020). «Different Types of Binary Tree with colourful illustrations». Medium (στα Αγγλικά). Ανακτήθηκε στις 24 Ιανουαρίου 2020.
Mehta, Dinesh· Sartaj Sahni (2004). Handbook of Data Structures and Applications. Chapman and Hall. ISBN 1-58488-435-5.
Βιβλιογραφία
Donald Knuth . Η τέχνη του προγραμματισμού υπολογιστών τόμος 1. Θεμελιώδεις Αλγόριθμοι , Τρίτη έκδοση. Addison-Wesley, 1997. (ISBN 0-201-89683-4) ISBN 0-201-89683-4 . Το τμήμα 2.3, ιδιαίτερα τα σημεία 2.3.1-2.3.2 (σελ. 318-348).
Hellenica World - Scientific Library
Από τη ελληνική Βικιπαίδεια http://el.wikipedia.org . Όλα τα κείμενα είναι διαθέσιμα υπό την GNU Free Documentation License