.

Zeno's Paradoxa such as the Achilles and the tortoise were the reason that ancient Greeks tried to avoid the Infinite. Common logic is that parts of a set are less than all the parts of it.

A set is a collection of objects called the elements of the set. How many parts has a set? We have just to count these. But was is counting? Consider the set (A,B,C). We know that there are 3 elements A, B and C. Counting is a mapping to the the natural numbers. For example 1 -> A, 2-> B and 3-> C. We can say that the set (A,B,C) has 3 elements as we can find a mapping to the subset (1,2,3) of the natural numbers. We could used a different mapping such as 1-> C, 2->A, 3->B, but this doesn't matter. We think that the natural numbers 1,2,3,...are infinite large. For every number n there is a larger number n+1 and there is no apparent end. Like in Archytas Thought Experiment about the size of the Universe there is no end and we say that we have an infinite set. But is it true that the subsets of this sets are less numerous than the entire set? Consider all the even numbers 2,4,6,8.... and all the natural numbers 1,2,3,4,.... We may think that there are more natural numbers than even natural numbers since the even numbers are a subset. But is this true? Let us count the number of even natural numbers. We have to find a mapping from the natural numbers to the even natural numbers. For each natural number m there is a even natural number 2m. Therefore there are as many even number as there are even and odd numbers!

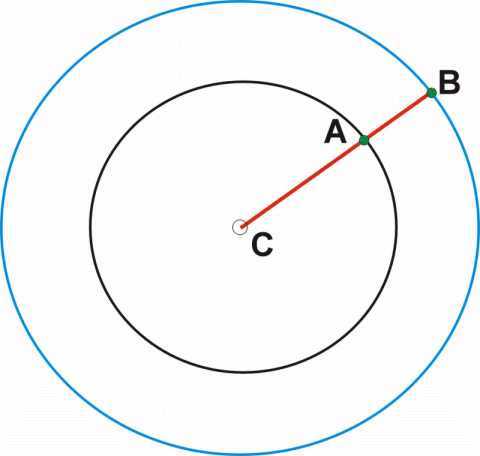
Consider the 2 concentric circles in the Figure above. Has the larger outer circle more points than the smaller circle? We think that the answer is probably yes! But is this true? We have to count the number of points in both circles. If we can find a mapping that assigns for each point on the larger circle a point in the smaller circle then both circles have the same number of points. Every point B of the larger circle can be connected with a line going through the center. This line will pass through a point A of the smaller circle. We could consider this as the mapping that we wanted. Every point of the larger circle can be mapped to a point on the smaller circle. How is this possible? Should the larger circle not contain more points than the smaller circle? The point A can be very close to the point C.

So we have to recognize that our common logic does not work for the infinite large sets. Aristotle considering the Paradox due to the infinite small and large considered two types of infinities. The so-called “actual” infinite and the “potential” infinite.

If we have to travel a distance then we do not travel over a actual infinite set which is impossible but we travel over a potential infinite set in that this set could be divided actually for ever in smaller and smaller pieces. It was actually considered that the for real objects the actual infinite is not possible, that an object could not have something which exceeds all limits. An actual infinity is regarded as a completed totality. A potential infinity is more like a finite but indefinitely long, unending series of events. According to Aristotle, actual infinities cannot exist, but potential infinities exist in nature and are manifested to us in various ways, for instance the indefinite cycle of the seasons or the indefinite divisibility of a piece of matter.

What are the problems according to Aristotle for things such as a infinite Universe as Archytas believes with his “Thought Experiment”?

1. A body is defined as that which is bounded by a surface, therefore there cannot be an infinite body.

2. A number, by definition, is countable, so there is no number called ‘infinity’.

3. Perceptible bodies exist somewhere, they have a place, so there cannot be an infinite body.

But we also cannot say that the infinite does not exist according to Aristotle here are some reasons:

1. If no infinite, magnitudes will not be divisible into magnitudes, but magnitudes can be divisible into magnitudes (potentially infinitely), therefore an infinite in some sense exists.

2. If no infinite, number would not be infinite, but number is infinite (potentially), therefore infinity does exist in some sense.

Is the Universe a body? Is the infinite a number? Aristotle had to argue that the universe is finite to avoid infinite circular velocities at the periphery in his earth centric model. This is another reason why he rejected the idea of uniform motion in a straight line, because it would have implied the concept of an infinite straight line, which is not permitted in a finite universe.

The problem of the actual infinite becomes a problem with Newtons calculus but only Augustin Louis Cauchy and Karl Weierstrass considered mathematical strict the problems in differentiation and integration of infinitesimal small quantities.

It was Cantor who considered the problems of infinite sets. Against common logic that infinite is something unlimited and larger than anything he discovered that there are sets larger than the infinite sets of natural numbers. He also showed that no infinite set could have as many elements as all possible subsets.

In this way he showed that there are sets infinite larger than the sets of the infinite natural numbers. He arranged all the subsets and the elements of the sets in the form of a table and showed using the diagonal of the table that such a mapping is not possible. In this way we have a similarity with the Pythagorean discovery that the diagonal of a square cannot be described as a ratio of natural numbers as there is no such ratio for the square root of the number 2. In this way actually the ancient Greeks discovered that there is no mapping of the natural to the real numbers that are more infinite than the infinite natural numbers 1,2,3,... etc.

Cantor Relief

Aristotle and why an infinite large body cannot have a finite weight:

From what we have said, then, it is clear that the weight of the infinite body cannot be finite. It must then be infinite. We have therefore only to show this to be impossible in order to prove an infinite body impossible. But the impossibility of infinite weight can be shown in the following way. A given weight moves a given distance in a given time; a weight which is as great and more moves the same distance in a less time, the times being in inverse proportion to the weights. For instance, if one weight is twice another, it will take half as long over a given movement. Further, a finite weight traverses any finite distance in a finite time. It necessarily follows from this that infinite weight, if there is such a thing, being, on the one hand, as great and more than as great as the finite, will move accordingly, but being, on the other hand, compelled to move in a time inversely proportionate to its greatness, cannot move at all. The time should be less in proportion as the weight is greater. But there is no proportion between the infinite and the finite: proportion can only hold between a less and a greater finite time. And though you may say that the time of the movement can be continually diminished, yet there is no minimum. Nor, if there were, would it help us. For some finite body could have been found greater than the given finite in the same proportion which is supposed to hold between the infinite and the given finite; so that an infinite and a finite weight must have traversed an equal distance in equal time. But that is impossible. Again, whatever the time, so long as it is finite, in which the infinite performs the motion, a finite weight must necessarily move a certain finite distance in that same time. Infinite weight is therefore impossible, and the same reasoning applies also to infinite lightness. Bodies then of infinite weight and of infinite lightness are equally impossible. Aristotle, De Caelo I Part 6, 273b 27 - 274a 19

Melissos an admiral , son of Ithagenes born 490-80 BC in Samos a Philosopher from the Eleatic school said:

If something exists it is eternal because nothing can be produced from nothing

If something is eternal it is infinite because it cannot have an end and a beginning

If something is eternal and infinite it is one since otherwise one part could cover or limit the others

If something is eternal infinite and unique then it is also not movable since there is no place in which it could move

From Alexander and Anton Zenkins, comments of Mathematicians and Philosophers about the infinite and Cantors ideas:

ARISTOTLE: "There will not be an actual infinite. The infinite has a potential existence.";
GAUSS: "I must protest most vehemently against <the> use of the infinite as something consummated, as this is never permitted in mathematics";
KRONECKER: "I don't know what predominates in Cantor's theory - philosophy or theology, but I am sure that there is no mathematics there";
POINCARE: "There is no actual infinity; Cantorians forgot that and fell into contradictions. Later generations will regard Mengenlehre as a disease from which one has recovered ";
BROUWER: Cantor's theory as a whole is "a pathological incident in history of mathematics from which future generations will be horrified";
WITTGENSTEIN: “Cantor's argument has no deductive content at all”;
WEYL: the axiomatic set theory is a “house built on sand”;
P.VOPENKA: “the set theory whose energies were directed to the actualization of potential infinity turned out not to be able to eliminate the potentiality. . .”, and a lot of others.