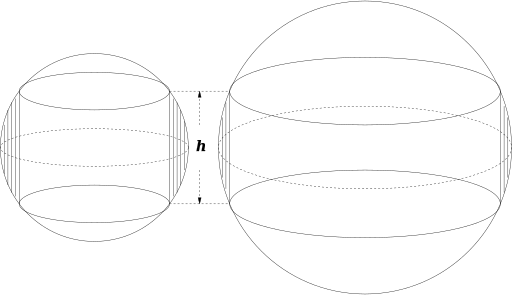
In geometry, the napkin-ring problem involves finding the volume of a "band" of specified height around a sphere, i.e. the part that remains after a hole in the shape of a circular cylinder is drilled through the center of the sphere. It is a counterintuitive fact that this volume does not depend on the original sphere's radius but only on the resulting band's height.
If a hole of height h is drilled straight through the center of a sphere, the volume of the remaining band does not depend on the size of the sphere. For a larger sphere, the band will be thinner but longer.
The problem is so called because after removing a cylinder from the sphere, the remaining band resembles the shape of a napkin ring.
Animation of a cut napkin ring with constant height
Statement
Suppose that the axis of a right circular cylinder passes through the center of a sphere of radius R and that h represents the height (defined as the distance in a direction parallel to the axis) of the part of the cylinder that is inside the sphere. The "band" is the part of the sphere that is outside the cylinder. The volume of the band depends on h but not on R:
\( V={\frac {\pi h^{3}}{6}}. \)
As the radius R of the sphere shrinks, the diameter of the cylinder must also shrink in order that h can remain the same. The band gets thicker, and this would increase its volume. But it also gets shorter in circumference, and this would decrease its volume. The two effects exactly cancel each other out. In the extreme case of the smallest possible sphere, the cylinder vanishes (its radius becomes zero) and the height h equals the diameter of the sphere. In this case the volume of the band is the volume of the whole sphere, which matches the formula given above.
An early study of this problem was written by 17th-century Japanese mathematician Seki Kōwa. According to Smith & Mikami (1914), Seki called this solid an arc-ring, or in Japanese kokan or kokwan.
Proof
Suppose the radius of the sphere is R {\displaystyle R} R and the length of the cylinder (or the tunnel) is h {\displaystyle h} h.
By the Pythagorean theorem, the radius of the cylinder is
Finding the measurements of the ring that is the horizontal cross-section.
\( {\sqrt {R^{2}-\left({\frac {h}{2}}\right)^{2}}},\qquad \qquad (1) \)
and the radius of the horizontal cross-section of the sphere at height y above the "equator" is
\( {\displaystyle {\sqrt {R^{2}-y^{2}}}.\qquad \qquad (2)} \)
The cross-section of the band with the plane at height y is the region inside the larger circle of radius given by (2) and outside the smaller circle of radius given by (1). The cross-section's area is therefore the area of the larger circle minus the area of the smaller circle:
\( {\begin{aligned}&{}\quad \pi ({\text{larger radius}})^{2}-\pi ({\text{smaller radius}})^{2}\\&=\pi \left({\sqrt {R^{2}-y^{2}}}\right)^{2}-\pi \left({\sqrt {R^{2}-\left({\frac {h}{2}}\right)^{2}\,{}}}\,\right)^{2}=\pi \left(\left({\frac {h}{2}}\right)^{2}-y^{2}\right).\end{aligned}} \)
The radius R does not appear in the last quantity. Therefore, the area of the horizontal cross-section at height y does not depend on R, as long as y ≤ h/2 ≤ R. The volume of the band is
\( \int _{{-h/2}}^{{h/2}}({\text{area of cross-section at height }}y)\,dy,\)
and that does not depend on R.
This is an application of Cavalieri's principle: volumes with equal-sized corresponding cross-sections are equal. Indeed, the area of the cross-section is the same as that of the corresponding cross-section of a sphere of radius h/2, which has volume
\( {\frac {4}{3}}\pi \left({\frac {h}{2}}\right)^{3}={\frac {\pi h^{3}}{6}}.
See also
Visual calculus, an intuitive way to solve this type of problem, originally applied to finding the area of an annulus, given only its chord length
String girdling Earth, another problem where the radius of a sphere or circle is counter-intuitively irrelevant
References
Devlin, Keith (2008), The Napkin Ring Problem, Mathematical Association of America, archived from the original on 11 August 2011, retrieved 25 February 2009
Devlin, Keith (2008), Lockhart's Lament, Mathematical Association of America, archived from the original on 11 August 2011, retrieved 25 February 2009
Gardner, Martin (1994), "Hole in the Sphere", My best mathematical and logic puzzles, Dover Publications, p. 8
Jones, Samuel I. (1912), Mathematical Wrinkles for Teachers and Private Learners, Norwood, MA: J. B. Cushing Co. Problem 132 asks for the volume of a sphere with a cylindrical hole drilled through it, but does not note the invariance of the problem under changes of radius.
Levi, Mark (2009), "6.3 How Much Gold Is in a Wedding Ring?", The Mathematical Mechanic: Using Physical Reasoning to Solve Problems, Princeton University Press, pp. 102–104, ISBN 978-0-691-14020-9. Levi argues that the volume depends only on the height of the hole based on the fact that the ring can be swept out by a half-disk with the height as its diameter.
Lines, L. (1965), Solid geometry: With Chapters on Space-lattices, Sphere-packs and Crystals, Dover. Reprint of 1935 edition. A problem on page 101 describes the shape formed by a sphere with a cylinder removed as a "napkin ring" and asks for a proof that the volume is the same as that of a sphere with diameter equal to the length of the hole.
Pólya, George (1990), Mathematics and Plausible Reasoning, Vol. I: Induction and Analogy in Mathematics, Princeton University Press, pp. 191–192. Reprint of 1954 edition.
Smith, David E.; Mikami, Yoshio (1914), A History of Japanese Mathematics, Open Court Publishing Company, pp. 121–123. Republished by Dover, 2004, ISBN 0-486-43482-6. Smith and Mikami discuss the napkin ring problem in the context of two manuscripts of Seki on the mensuration of solids, Kyuseki and Kyuketsu Hengyo So.
Undergraduate Texts in Mathematics
Graduate Studies in Mathematics
Hellenica World - Scientific Library
Retrieved from "http://en.wikipedia.org/"
All text is available under the terms of the GNU Free Documentation License