The concept of a lattice arises in order theory, a branch of mathematics. The Hasse diagram below depicts the inclusion relationships among some important subclasses of lattices.
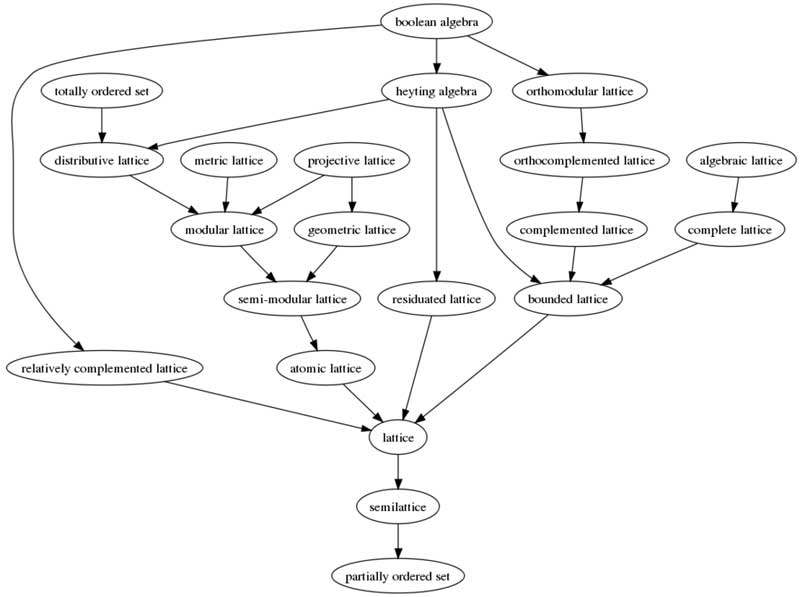
Proofs of the relationships in the map
1. A boolean algebra is a complemented distributive lattice. (def)
2. A boolean algebra is a heyting algebra.[1]
3. A boolean algebra is orthocomplemented.[2]
4. A distributive orthocomplemented lattice is orthomodular.[3]
5. A boolean algebra is orthomodular. (1,3,4)
6. An orthomodular lattice is orthocomplemented. (def)
7. An orthocomplemented lattice is complemented. (def)
8. A complemented lattice is bounded. (def)
9. An algebraic lattice is complete. (def)
10. A complete lattice is bounded.
11. A heyting algebra is bounded. (def)
12. A bounded lattice is a lattice. (def)
13. A heyting algebra is residuated.
14. A residuated lattice is a lattice. (def)
15. A distributive lattice is modular.[4]
16. A modular complemented lattice is relatively complemented.[5]
17. A boolean algebra is relatively complemented. (1,15,16)
18. A relatively complemented lattice is a lattice. (def)
19. A heyting algebra is distributive.[6]
20. A totally ordered set is a distributive lattice.
21. A metric lattice is modular.[7]
22. A modular lattice is semi-modular.[8]
23. A projective lattice is modular.[9]
24. A projective lattice is geometric. (def)
25. A geometric lattice is semi-modular.[10]
26. A semi-modular lattice is atomic.[11][disputed – discuss]
27. An atomic lattice is a lattice. (def)
28. A lattice is a semi-lattice. (def)
29. A semi-lattice is a partially ordered set. (def)
Notes
Rutherford (1965), p.77.
Rutherford (1965), p.32-33.
PlanetMath: orthomodular lattice Archived 2007-10-11 at the Wayback Machine
Rutherford (1965), p.22.
Rutherford (1965), p.31.
Rutherford (1965), Th.25.1 p.74.
Rutherford (1965), Th.8.1 p.22.
Rutherford (1965), p.87.
Rutherford (1965), p.94.
Rutherford (1965), Th.32.1 p.92.
Rutherford (1965), p.89.
References
Rutherford, Daniel Edwin (1965). Introduction to Lattice Theory. Oliver and Boyd.
Undergraduate Texts in Mathematics
Graduate Studies in Mathematics
Hellenica World - Scientific Library
Retrieved from "http://en.wikipedia.org/"
All text is available under the terms of the GNU Free Documentation License

