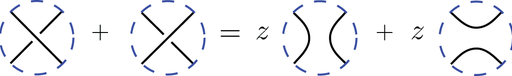In knot theory, the Kauffman polynomial is a 2-variable knot polynomial due to Louis Kauffman.[1] It is initially defined on a link diagram as
\( F(K)(a,z)=a^{{-w(K)}}L(K)\,, \)
where w(K) is the writhe of the link diagram and L(K) is a polynomial in a and z defined on link diagrams by the following properties:
L(O)=1 (O is the unknot).
\( L(s_{r})=aL(s),\qquad L(s_{\ell })=a^{{-1}}L(s). \)
L is unchanged under type II and III Reidemeister moves.
Here s is a strand and \( s_{r} \) (resp. \( s_{\ell } \) ) is the same strand with a right-handed (resp. left-handed) curl added (using a type I Reidemeister move).
Additionally L must satisfy Kauffman's skein relation:
The pictures represent the L polynomial of the diagrams which differ inside a disc as shown but are identical outside.
Kauffman showed that L exists and is a regular isotopy invariant of unoriented links. It follows easily that F is an ambient isotopy invariant of oriented links.
The Jones polynomial is a special case of the Kauffman polynomial, as the L polynomial specializes to the bracket polynomial. The Kauffman polynomial is related to Chern–Simons gauge theories for SO(N) in the same way that the HOMFLY polynomial is related to Chern–Simons gauge theories for SU(N).[2]
References
Kauffman, Louis (1990). "An invariant of regular isotopy" (PDF). Transactions of the American Mathematical Society. 318 (2): 417–471. doi:10.1090/S0002-9947-1990-0958895-7. MR 0958895.
Witten, Edward (1989). "Quantum field theory and the Jones polynomial". Communications in Mathematical Physics. 121 (3): 351–399. doi:10.1007/BF01217730. MR 0990772.
Further reading
Kauffman, Louis (1987). On Knots. Annals of Mathematics Studies. 115. Princeton, NJ: Princeton University Press. ISBN 0-691-08435-1. MR 0907872.
External links
"Entry for Kauffman polynomial". Springer EoM.
"The Kauffman Polynomial", The Knot Atlas.
vte
Knot theory (knots and links)
Hyperbolic
Figure-eight (41) Three-twist (52) Stevedore (61) 62 63 Endless (74) Carrick mat (818) Perko pair (10161) (−2,3,7) pretzel (12n242) Whitehead (52
1) Borromean rings (63
2) L10a140
Satellite
Composite knots
Granny Square Knot sum
Torus
Unknot (01) Trefoil (31) Cinquefoil (51) Septafoil (71) Unlink (02
1) Hopf (22
1) Solomon's (42
1)
Invariants
Alternating Arf invariant Bridge no.
2-bridge Brunnian Chirality
Invertible Crosscap no. Crossing no. Finite type invariant Hyperbolic volume Khovanov homology Genus Knot group Link group Linking no. Polynomial
Alexander Bracket HOMFLY Jones Kauffman Pretzel Prime
list Stick no. Tricolorability Unknotting no. and problem
Notation
and operations
Alexander–Briggs notation Conway notation Dowker notation Flype Mutation Reidemeister move Skein relation Tabulation
Other
Alexander's theorem Berge Braid theory Conway sphere Complement Double torus Fibered Knot List of knots and links Ribbon Slice Sum Tait conjectures Twist Wild Writhe Surgery theory
Undergraduate Texts in Mathematics
Graduate Studies in Mathematics
Hellenica World - Scientific Library
Retrieved from "http://en.wikipedia.org/"
All text is available under the terms of the GNU Free Documentation License