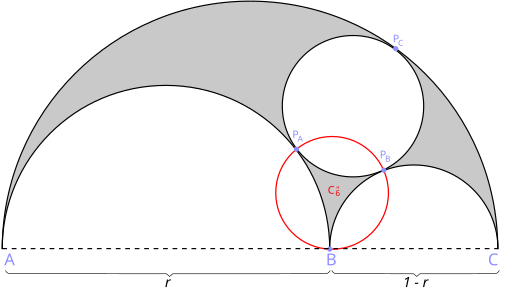
In geometry, the Bankoff circle or Bankoff triplet circle is a certain Archimedean circle that can be constructed from an arbelos; an Archimedean circle is any circle with area equal to each of Archimedes' twin circles. The Bankoff circle was first constructed by Leon Bankoff in 1974.[1][2][3]
Construction
The Bankoff circle is formed from three semicircles that create an arbelos. A circle C1 is then formed tangent to each of the three semicircles, as an instance of the problem of Apollonius. Another circle C2 is then created, through three points: the two points of tangency of C1 with the smaller two semicircles, and the point where the two smaller semicircles are tangent to each other. C2 is the Bankoff circle.
Radius of the circle
If r = AB/AC, then the radius of the Bankoff circle is:
\( R={\frac {1}{2}}r\left(1-r\right). \)
References
Bankoff, L. (1974), "Are the twin circles of Archimedes really twins?", Mathematics Magazine, 47: 214–218, JSTOR 2689213.
Dodge, Clayton W.; Schoch, Thomas; Woo, Peter Y.; Yiu, Paul (1999), "Those ubiquitous Archimedean circles", Mathematics Magazine, 72 (3): 202–213, JSTOR 2690883.
Čerin, Zvonko (2006), "Configurations on centers of Bankoff circles" (PDF), Far East Journal of Mathematical Sciences, 22 (3): 305–320, archived from the original (PDF) on 2011-07-21.
External links
Weisstein, Eric W. "Bankoff Circle". MathWorld.
Bankoff Circle by Jay Warendorff, the Wolfram Demonstrations Project.
Online catalogue of Archimedean circles, Floor van Lamoen.
Undergraduate Texts in Mathematics
Graduate Studies in Mathematics
Hellenica World - Scientific Library
Retrieved from "http://en.wikipedia.org/"
All text is available under the terms of the GNU Free Documentation License