In 5-dimensional geometry, there are 31 uniform polytopes with B5 symmetry. There are two regular forms, the 5-orthoplex, and 5-cube with 10 and 32 vertices respectively. The 5-demicube is added as an alternation of the 5-cube.
They can be visualized as symmetric orthographic projections in Coxeter planes of the B5 Coxeter group, and other subgroups.
Graphs
Symmetric orthographic projections of these 32 polytopes can be made in the B5, B4, B3, B2, A3, Coxeter planes. Ak has [k+1] symmetry, and Bk has [2k] symmetry.
These 32 polytopes are each shown in these 5 symmetry planes, with vertices and edges drawn, and vertices colored by the number of overlapping vertices in each projective position.
| Graph B5 / A4 [10] |
Graph B4 / D5 [8] |
Graph B3 / A2 [6] |
Graph B2 [4] |
Graph A3 [4] |
Coxeter-Dynkin diagram and Schläfli symbol Johnson and Bowers names |
|
|---|---|---|---|---|---|---|
| 1 |  |
 |
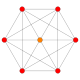 |
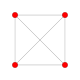 |
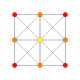 |
h{4,3,3,3} 5-demicube Hemipenteract (hin) |
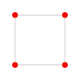
| 2 |  |
 |
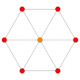 |
 |
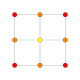 |
{4,3,3,3} 5-cube Penteract (pent) |
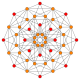
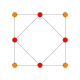
| 3 |  |
 |
 |
 |
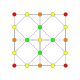 |
t1{4,3,3,3} = r{4,3,3,3} Rectified 5-cube Rectified penteract (rin) |
| 4 |  |
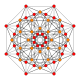 |
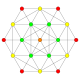 |
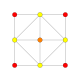 |
 |
t2{4,3,3,3} = 2r{4,3,3,3} Birectified 5-cube Penteractitriacontiditeron (nit) |
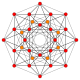
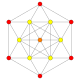
| 5 |  |
 |
 |
 |
 |
t1{3,3,3,4} = r{3,3,3,4} Rectified 5-orthoplex Rectified triacontiditeron (rat) |
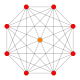
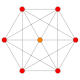
| 6 |  |
 |
 |
 |
 |
{3,3,3,4} 5-orthoplex Triacontiditeron (tac) |
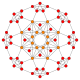
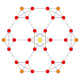
| 7 |  |
 |
 |
 |
 |
t0,1{4,3,3,3} = t{3,3,3,4} Truncated 5-cube Truncated penteract (tan) |
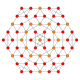
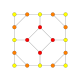
| 8 |  |
 |
 |
 |
 |
t1,2{4,3,3,3} = 2t{4,3,3,3} Bitruncated 5-cube Bitruncated penteract (bittin) |
| 9 |  |
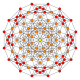 |
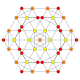 |
 |
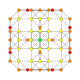 |
t0,2{4,3,3,3} = rr{4,3,3,3} Cantellated 5-cube Rhombated penteract (sirn) |
| 10 |  |
 |
 |
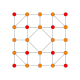 |
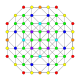 |
t1,3{4,3,3,3} = 2rr{4,3,3,3} Bicantellated 5-cube Small birhombi-penteractitriacontiditeron (sibrant) |
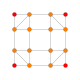
| 11 | 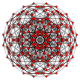 |
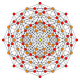 |
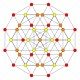 |
 |
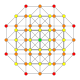 |
t0,3{4,3,3,3} Runcinated 5-cube Prismated penteract (span) |
| 12 |  |
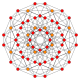 |
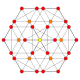 |
 |
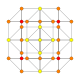 |
t0,4{4,3,3,3} = 2r2r{4,3,3,3} Stericated 5-cube Small celli-penteractitriacontiditeron (scant) |
| 13 |  |
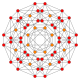 |
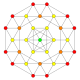 |
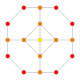 |
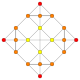 |
t0,1{3,3,3,4} = t{3,3,3,4} Truncated 5-orthoplex Truncated triacontiditeron (tot) |
| 14 |  |
 |
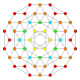 |
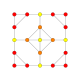 |
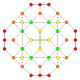 |
t1,2{3,3,3,4} = 2t{3,3,3,4} Bitruncated 5-orthoplex Bitruncated triacontiditeron (bittit) |
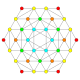
| 15 |  |
 |
 |
 |
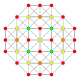 |
t0,2{3,3,3,4} = rr{3,3,3,4} Cantellated 5-orthoplex Small rhombated triacontiditeron (sart) |
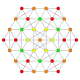
| 16 |  |
 |
 |
 |
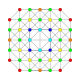 |
t0,3{3,3,3,4} Runcinated 5-orthoplex Small prismated triacontiditeron (spat) |
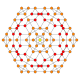
| 17 |  |
 |
 |
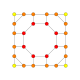 |
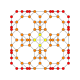 |
t0,1,2{4,3,3,3} = tr{4,3,3,3} Cantitruncated 5-cube Great rhombated penteract (girn) |
| 18 |  |
 |
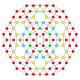 |
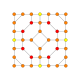 |
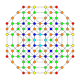 |
t1,2,3{4,3,3,3} = tr{4,3,3,3} Bicantitruncated 5-cube Great birhombi-penteractitriacontiditeron (gibrant) |
| 19 |  |
 |
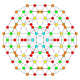 |
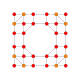 |
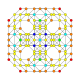 |
t0,1,3{4,3,3,3} Runcitruncated 5-cube Prismatotruncated penteract (pattin) |
| 20 |  |
 |
 |
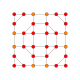 |
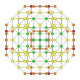 |
t0,2,3{4,3,3,3} Runcicantellated 5-cube Prismatorhomated penteract (prin) |
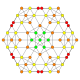
| 21 |  |
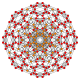 |
 |
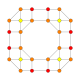 |
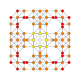 |
t0,1,4{4,3,3,3} Steritruncated 5-cube Cellitruncated penteract (capt) |
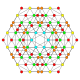
| 22 |  |
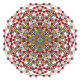 |
 |
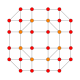 |
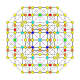 |
t0,2,4{4,3,3,3} Stericantellated 5-cube Cellirhombi-penteractitriacontiditeron (carnit) |
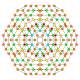
| 23 |  |
 |
 |
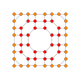 |
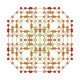 |
t0,1,2,3{4,3,3,3} Runcicantitruncated 5-cube Great primated penteract (gippin) |
| 24 |  |
 |
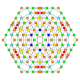 |
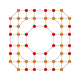 |
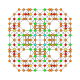 |
t0,1,2,4{4,3,3,3} Stericantitruncated 5-cube Celligreatorhombated penteract (cogrin) |
| 25 |  |
 |
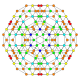 |
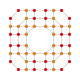 |
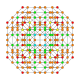 |
t0,1,3,4{4,3,3,3} Steriruncitruncated 5-cube Celliprismatotrunki-penteractitriacontiditeron (captint) |
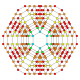
| 26 |  |
 |
 |
 |
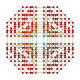 |
t0,1,2,3,4{4,3,3,3} Omnitruncated 5-cube Great celli-penteractitriacontiditeron (gacnet) |
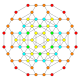
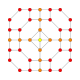
| 27 |  |
 |
 |
 |
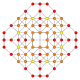 |
t0,1,2{3,3,3,4} = tr{3,3,3,4} Cantitruncated 5-orthoplex Great rhombated triacontiditeron (gart) |
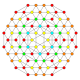
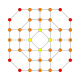
| 28 |  |
 |
 |
 |
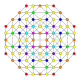 |
t0,1,3{3,3,3,4} Runcitruncated 5-orthoplex Prismatotruncated triacontiditeron (pattit) |
| 29 |  |
 |
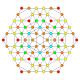 |
 |
 |
t0,2,3{3,3,3,4} Runcicantellated 5-orthoplex Prismatorhombated triacontiditeron (pirt) |
| 30 |  |
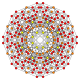 |
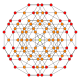 |
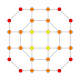 |
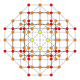 |
t0,1,4{3,3,3,4} Steritruncated 5-orthoplex Cellitruncated triacontiditeron (cappin) |
| 31 |  |
 |
 |
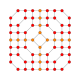 |
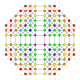 |
t0,1,2,3{3,3,3,4} Runcicantitruncated 5-orthoplex Great prismatorhombated triacontiditeron (gippit) |
| 32 |  |
 |
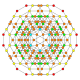 |
 |
 |
t0,1,2,4{3,3,3,4} Stericantitruncated 5-orthoplex Celligreatorhombated triacontiditeron (cogart) |
References
H.S.M. Coxeter:
H.S.M. Coxeter, Regular Polytopes, 3rd Edition, Dover New York, 1973
Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6[1]
(Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
(Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591]
(Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. Dissertation, University of Toronto, 1966
Notes
Wiley::Kaleidoscopes: Selected Writings of H.S.M. Coxeter
|
Fundamental convex regular and uniform polytopes in dimensions 2–10
|
||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Family | An | Bn | I2(p) / Dn | E6 / E7 / E8 / F4 / G2 | Hn | |||||||
| Regular polygon | Triangle | Square | p-gon | Hexagon | Pentagon | |||||||
| Uniform polyhedron | Tetrahedron | Octahedron • Cube | Demicube | Dodecahedron • Icosahedron | ||||||||
| Uniform 4-polytope | 5-cell | 16-cell • Tesseract | Demitesseract | 24-cell | 120-cell • 600-cell | |||||||
| Uniform 5-polytope | 5-simplex | 5-orthoplex • 5-cube | 5-demicube | |||||||||
| Uniform 6-polytope | 6-simplex | 6-orthoplex • 6-cube | 6-demicube | 122 • 221 | ||||||||
| Uniform 7-polytope | 7-simplex | 7-orthoplex • 7-cube | 7-demicube | 132 • 231 • 321 | ||||||||
| Uniform 8-polytope | 8-simplex | 8-orthoplex • 8-cube | 8-demicube | 142 • 241 • 421 | ||||||||
| Uniform 9-polytope | 9-simplex | 9-orthoplex • 9-cube | 9-demicube | |||||||||
| Uniform 10-polytope | 10-simplex | 10-orthoplex • 10-cube | 10-demicube | |||||||||
| Uniform n-polytope | n-simplex | n-orthoplex • n-cube | n-demicube | 1k2 • 2k1 • k21 | n-pentagonal polytope | |||||||
| Topics: Polytope families • Regular polytope • List of regular polytopes and compounds | ||||||||||||
Undergraduate Texts in Mathematics
Graduate Studies in Mathematics
Hellenica World - Scientific Library
Retrieved from "http://en.wikipedia.org/"
All text is available under the terms of the GNU Free Documentation License

