A8 polytope

In 8-dimensional geometry, there are 135 uniform polytopes with A8 symmetry. There is one self-dual regular form, the 8-simplex with 9 vertices.

Each can be visualized as symmetric orthographic projections in Coxeter planes of the A8 Coxeter group, and other subgroups.

Graphs

Symmetric orthographic projections of these 135 polytopes can be made in the A8, A7, A6, A5, A4, A3, A2 Coxeter planes. Ak has [k+1] symmetry.

These 135 polytopes are each shown in these 7 symmetry planes, with vertices and edges drawn, and vertices colored by the number of overlapping vertices in each projective position.

#	Coxeter-Dynkin diagram Schläfli symbol Johnson name	Ak orthogonal projection graphs
		A8 [9]	A7 [8]	A6 [7]	A5 [6]	A4 [5]	A3 [4]	A2 [3]
1	t0{3,3,3,3,3,3,3} 8-simplex
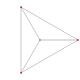2	t1{3,3,3,3,3,3,3} Rectified 8-simplex
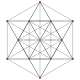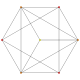3	t2{3,3,3,3,3,3,3} Birectified 8-simplex
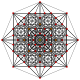4	t3{3,3,3,3,3,3,3} Trirectified 8-simplex
5	t0,1{3,3,3,3,3,3,3} Truncated 8-simplex
6	t0,2{3,3,3,3,3,3,3} Cantellated 8-simplex
7	t1,2{3,3,3,3,3,3,3} Bitruncated 8-simplex
8	t0,3{3,3,3,3,3,3,3} Runcinated 8-simplex
9	t1,3{3,3,3,3,3,3,3} Bicantellated 8-simplex
10	t2,3{3,3,3,3,3,3,3} Tritruncated 8-simplex
11	t0,4{3,3,3,3,3,3,3} Stericated 8-simplex
12	t1,4{3,3,3,3,3,3,3} Biruncinated 8-simplex
13	t2,4{3,3,3,3,3,3,3} Tricantellated 8-simplex
14	t3,4{3,3,3,3,3,3,3} Quadritruncated 8-simplex
15	t0,5{3,3,3,3,3,3,3} Pentellated 8-simplex
16	t1,5{3,3,3,3,3,3,3} Bistericated 8-simplex
17	t2,5{3,3,3,3,3,3,3} Triruncinated 8-simplex
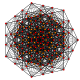
18	t0,6{3,3,3,3,3,3,3} Hexicated 8-simplex
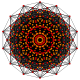
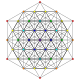
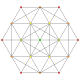
19	t1,6{3,3,3,3,3,3,3} Bipentellated 8-simplex
20	t0,7{3,3,3,3,3,3,3} Heptellated 8-simplex
21	t0,1,2{3,3,3,3,3,3,3} Cantitruncated 8-simplex
22	t0,1,3{3,3,3,3,3,3,3} Runcitruncated 8-simplex
23	t0,2,3{3,3,3,3,3,3,3} Runcicantellated 8-simplex
24	t1,2,3{3,3,3,3,3,3,3} Bicantitruncated 8-simplex
25	t0,1,4{3,3,3,3,3,3,3} Steritruncated 8-simplex
26	t0,2,4{3,3,3,3,3,3,3} Stericantellated 8-simplex
27	t1,2,4{3,3,3,3,3,3,3} Biruncitruncated 8-simplex
28	t0,3,4{3,3,3,3,3,3,3} Steriruncinated 8-simplex
29	t1,3,4{3,3,3,3,3,3,3} Biruncicantellated 8-simplex
30	t2,3,4{3,3,3,3,3,3,3} Tricantitruncated 8-simplex
31	t0,1,5{3,3,3,3,3,3,3} Pentitruncated 8-simplex
32	t0,2,5{3,3,3,3,3,3,3} Penticantellated 8-simplex
33	t1,2,5{3,3,3,3,3,3,3} Bisteritruncated 8-simplex
34	t0,3,5{3,3,3,3,3,3,3} Pentiruncinated 8-simplex
35	t1,3,5{3,3,3,3,3,3,3} Bistericantellated 8-simplex
36	t2,3,5{3,3,3,3,3,3,3} Triruncitruncated 8-simplex
37	t0,4,5{3,3,3,3,3,3,3} Pentistericated 8-simplex
38	t1,4,5{3,3,3,3,3,3,3} Bisteriruncinated 8-simplex
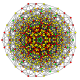39	t0,1,6{3,3,3,3,3,3,3} Hexitruncated 8-simplex
40	t0,2,6{3,3,3,3,3,3,3} Hexicantellated 8-simplex
41	t1,2,6{3,3,3,3,3,3,3} Bipentitruncated 8-simplex
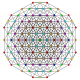42	t0,3,6{3,3,3,3,3,3,3} Hexiruncinated 8-simplex
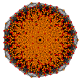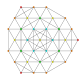43	t1,3,6{3,3,3,3,3,3,3} Bipenticantellated 8-simplex
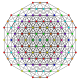44	t0,4,6{3,3,3,3,3,3,3} Hexistericated 8-simplex
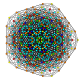45	t0,5,6{3,3,3,3,3,3,3} Hexipentellated 8-simplex
46	t0,1,7{3,3,3,3,3,3,3} Heptitruncated 8-simplex
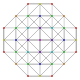47	t0,2,7{3,3,3,3,3,3,3} Hepticantellated 8-simplex
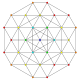48	t0,3,7{3,3,3,3,3,3,3} Heptiruncinated 8-simplex
49	t0,1,2,3{3,3,3,3,3,3,3} Runcicantitruncated 8-simplex
50	t0,1,2,4{3,3,3,3,3,3,3} Stericantitruncated 8-simplex
51	t0,1,3,4{3,3,3,3,3,3,3} Steriruncitruncated 8-simplex
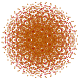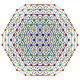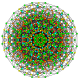52	t0,2,3,4{3,3,3,3,3,3,3} Steriruncicantellated 8-simplex
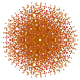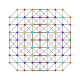53	t1,2,3,4{3,3,3,3,3,3,3} Biruncicantitruncated 8-simplex
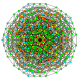54	t0,1,2,5{3,3,3,3,3,3,3} Penticantitruncated 8-simplex
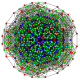55	t0,1,3,5{3,3,3,3,3,3,3} Pentiruncitruncated 8-simplex
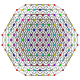56	t0,2,3,5{3,3,3,3,3,3,3} Pentiruncicantellated 8-simplex
57	t1,2,3,5{3,3,3,3,3,3,3} Bistericantitruncated 8-simplex
58	t0,1,4,5{3,3,3,3,3,3,3} Pentisteritruncated 8-simplex
59	t0,2,4,5{3,3,3,3,3,3,3} Pentistericantellated 8-simplex
60	t1,2,4,5{3,3,3,3,3,3,3} Bisteriruncitruncated 8-simplex
61	t0,3,4,5{3,3,3,3,3,3,3} Pentisteriruncinated 8-simplex
62	t1,3,4,5{3,3,3,3,3,3,3} Bisteriruncicantellated 8-simplex
63	t2,3,4,5{3,3,3,3,3,3,3} Triruncicantitruncated 8-simplex
64	t0,1,2,6{3,3,3,3,3,3,3} Hexicantitruncated 8-simplex
65	t0,1,3,6{3,3,3,3,3,3,3} Hexiruncitruncated 8-simplex
66	t0,2,3,6{3,3,3,3,3,3,3} Hexiruncicantellated 8-simplex
67	t1,2,3,6{3,3,3,3,3,3,3} Bipenticantitruncated 8-simplex
68	t0,1,4,6{3,3,3,3,3,3,3} Hexisteritruncated 8-simplex
69	t0,2,4,6{3,3,3,3,3,3,3} Hexistericantellated 8-simplex
70	t1,2,4,6{3,3,3,3,3,3,3} Bipentiruncitruncated 8-simplex
71	t0,3,4,6{3,3,3,3,3,3,3} Hexisteriruncinated 8-simplex
72	t1,3,4,6{3,3,3,3,3,3,3} Bipentiruncicantellated 8-simplex
73	t0,1,5,6{3,3,3,3,3,3,3} Hexipentitruncated 8-simplex
74	t0,2,5,6{3,3,3,3,3,3,3} Hexipenticantellated 8-simplex
75	t1,2,5,6{3,3,3,3,3,3,3} Bipentisteritruncated 8-simplex
76	t0,3,5,6{3,3,3,3,3,3,3} Hexipentiruncinated 8-simplex
77	t0,4,5,6{3,3,3,3,3,3,3} Hexipentistericated 8-simplex
78	t0,1,2,7{3,3,3,3,3,3,3} Hepticantitruncated 8-simplex
79	t0,1,3,7{3,3,3,3,3,3,3} Heptiruncitruncated 8-simplex
80	t0,2,3,7{3,3,3,3,3,3,3} Heptiruncicantellated 8-simplex
81	t0,1,4,7{3,3,3,3,3,3,3} Heptisteritruncated 8-simplex
82	t0,2,4,7{3,3,3,3,3,3,3} Heptistericantellated 8-simplex
83	t0,3,4,7{3,3,3,3,3,3,3} Heptisteriruncinated 8-simplex
84	t0,1,5,7{3,3,3,3,3,3,3} Heptipentitruncated 8-simplex
85	t0,2,5,7{3,3,3,3,3,3,3} Heptipenticantellated 8-simplex
86	t0,1,6,7{3,3,3,3,3,3,3} Heptihexitruncated 8-simplex
87	t0,1,2,3,4{3,3,3,3,3,3,3} Steriruncicantitruncated 8-simplex
88	t0,1,2,3,5{3,3,3,3,3,3,3} Pentiruncicantitruncated 8-simplex
89	t0,1,2,4,5{3,3,3,3,3,3,3} Pentistericantitruncated 8-simplex
90	t0,1,3,4,5{3,3,3,3,3,3,3} Pentisteriruncitruncated 8-simplex
91	t0,2,3,4,5{3,3,3,3,3,3,3} Pentisteriruncicantellated 8-simplex
92	t1,2,3,4,5{3,3,3,3,3,3,3} Bisteriruncicantitruncated 8-simplex
93	t0,1,2,3,6{3,3,3,3,3,3,3} Hexiruncicantitruncated 8-simplex
94	t0,1,2,4,6{3,3,3,3,3,3,3} Hexistericantitruncated 8-simplex
95	t0,1,3,4,6{3,3,3,3,3,3,3} Hexisteriruncitruncated 8-simplex
96	t0,2,3,4,6{3,3,3,3,3,3,3} Hexisteriruncicantellated 8-simplex
97	t1,2,3,4,6{3,3,3,3,3,3,3} Bipentiruncicantitruncated 8-simplex
98	t0,1,2,5,6{3,3,3,3,3,3,3} Hexipenticantitruncated 8-simplex
99	t0,1,3,5,6{3,3,3,3,3,3,3} Hexipentiruncitruncated 8-simplex
100	t0,2,3,5,6{3,3,3,3,3,3,3} Hexipentiruncicantellated 8-simplex
101	t1,2,3,5,6{3,3,3,3,3,3,3} Bipentistericantitruncated 8-simplex
102	t0,1,4,5,6{3,3,3,3,3,3,3} Hexipentisteritruncated 8-simplex
103	t0,2,4,5,6{3,3,3,3,3,3,3} Hexipentistericantellated 8-simplex
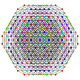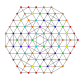104	t0,3,4,5,6{3,3,3,3,3,3,3} Hexipentisteriruncinated 8-simplex
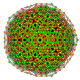105	t0,1,2,3,7{3,3,3,3,3,3,3} Heptiruncicantitruncated 8-simplex
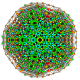106	t0,1,2,4,7{3,3,3,3,3,3,3} Heptistericantitruncated 8-simplex
107	t0,1,3,4,7{3,3,3,3,3,3,3} Heptisteriruncitruncated 8-simplex
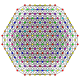108	t0,2,3,4,7{3,3,3,3,3,3,3} Heptisteriruncicantellated 8-simplex
109	t0,1,2,5,7{3,3,3,3,3,3,3} Heptipenticantitruncated 8-simplex
110	t0,1,3,5,7{3,3,3,3,3,3,3} Heptipentiruncitruncated 8-simplex
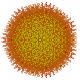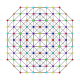111	t0,2,3,5,7{3,3,3,3,3,3,3} Heptipentiruncicantellated 8-simplex
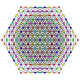112	t0,1,4,5,7{3,3,3,3,3,3,3} Heptipentisteritruncated 8-simplex
113	t0,1,2,6,7{3,3,3,3,3,3,3} Heptihexicantitruncated 8-simplex
114	t0,1,3,6,7{3,3,3,3,3,3,3} Heptihexiruncitruncated 8-simplex
115	t0,1,2,3,4,5{3,3,3,3,3,3,3} Pentisteriruncicantitruncated 8-simplex
116	t0,1,2,3,4,6{3,3,3,3,3,3,3} Hexisteriruncicantitruncated 8-simplex
117	t0,1,2,3,5,6{3,3,3,3,3,3,3} Hexipentiruncicantitruncated 8-simplex
118	t0,1,2,4,5,6{3,3,3,3,3,3,3} Hexipentistericantitruncated 8-simplex
119	t0,1,3,4,5,6{3,3,3,3,3,3,3} Hexipentisteriruncitruncated 8-simplex
120	t0,2,3,4,5,6{3,3,3,3,3,3,3} Hexipentisteriruncicantellated 8-simplex
121	t1,2,3,4,5,6{3,3,3,3,3,3,3} Bipentisteriruncicantitruncated 8-simplex
122	t0,1,2,3,4,7{3,3,3,3,3,3,3} Heptisteriruncicantitruncated 8-simplex
123	t0,1,2,3,5,7{3,3,3,3,3,3,3} Heptipentiruncicantitruncated 8-simplex
124	t0,1,2,4,5,7{3,3,3,3,3,3,3} Heptipentistericantitruncated 8-simplex
125	t0,1,3,4,5,7{3,3,3,3,3,3,3} Heptipentisteriruncitruncated 8-simplex
126	t0,2,3,4,5,7{3,3,3,3,3,3,3} Heptipentisteriruncicantellated 8-simplex
127	t0,1,2,3,6,7{3,3,3,3,3,3,3} Heptihexiruncicantitruncated 8-simplex
128	t0,1,2,4,6,7{3,3,3,3,3,3,3} Heptihexistericantitruncated 8-simplex
129	t0,1,3,4,6,7{3,3,3,3,3,3,3} Heptihexisteriruncitruncated 8-simplex
130	t0,1,2,5,6,7{3,3,3,3,3,3,3} Heptihexipenticantitruncated 8-simplex
131	t0,1,2,3,4,5,6{3,3,3,3,3,3,3} Hexipentisteriruncicantitruncated 8-simplex
132	t0,1,2,3,4,5,7{3,3,3,3,3,3,3} Heptipentisteriruncicantitruncated 8-simplex
133	t0,1,2,3,4,6,7{3,3,3,3,3,3,3} Heptihexisteriruncicantitruncated 8-simplex
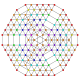134	t0,1,2,3,5,6,7{3,3,3,3,3,3,3} Heptihexipentiruncicantitruncated 8-simplex
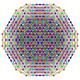135	t0,1,2,3,4,5,6,7{3,3,3,3,3,3,3} Omnitruncated 8-simplex

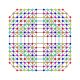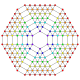References

H.S.M. Coxeter:
H.S.M. Coxeter, Regular Polytopes, 3rd Edition, Dover New York, 1973
Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
(Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
(Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591]
(Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. Dissertation, University of Toronto, 1966

External links

Klitzing, Richard. "8D uniform polytopes (polyzetta)".

Notes

Wiley::Kaleidoscopes: Selected Writings of H.S.M. Coxeter

Fundamental convex regular and uniform polytopes in dimensions 2–10
Family	An	Bn	I2(p) / Dn	E6 / E7 / E8 / F4 / G2	Hn
Regular polygon	Triangle	Square	p-gon	Hexagon	Pentagon
Uniform polyhedron	Tetrahedron	Octahedron • Cube	Demicube		Dodecahedron • Icosahedron
Uniform 4-polytope	5-cell	16-cell • Tesseract	Demitesseract	24-cell	120-cell • 600-cell
Uniform 5-polytope	5-simplex	5-orthoplex • 5-cube	5-demicube
Uniform 6-polytope	6-simplex	6-orthoplex • 6-cube	6-demicube	122 • 221
Uniform 7-polytope	7-simplex	7-orthoplex • 7-cube	7-demicube	132 • 231 • 321
Uniform 8-polytope	8-simplex	8-orthoplex • 8-cube	8-demicube	142 • 241 • 421
Uniform 9-polytope	9-simplex	9-orthoplex • 9-cube	9-demicube
Uniform 10-polytope	10-simplex	10-orthoplex • 10-cube	10-demicube
Uniform n-polytope	n-simplex	n-orthoplex • n-cube	n-demicube	1k2 • 2k1 • k21	n-pentagonal polytope
Topics: Polytope families • Regular polytope • List of regular polytopes and compounds

Undergraduate Texts in Mathematics

Graduate Texts in Mathematics

Graduate Studies in Mathematics

Mathematics Encyclopedia

World

Index

Hellenica World - Scientific Library

Retrieved from "http://en.wikipedia.org/"
All text is available under the terms of the GNU Free Documentation License