A4 polytope

In 4-dimensional geometry, there are 9 uniform polytopes with A4 symmetry. There is one self-dual regular form, the 5-cell with 5 vertices.

Symmetry

A4 symmetry, or [3,3,3] is order 120, with Conway quaternion notation +1/60[I×I].21. Its abstract structure is the symmetric group S5. Three forms with symmetric Coxeter diagrams have extended symmetry, [[3,3,3]] of order 240, and Conway notation ±1/60[I×I].2, and abstract structure S5×C2.
Visualizations

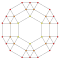
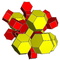
Each can be visualized as symmetric orthographic projections in Coxeter planes of the A4 Coxeter group, and other subgroups. Three Coxeter plane 2D projections are given, for the A4, A3, A2 Coxeter groups, showing symmetry order 5,4,3, and doubled on even Ak orders to 10,4,6 for symmetric Coxeter diagrams.

The 3D picture are drawn as Schlegel diagram projections, centered on the cell at pos. 3, with a consistent orientation, and the 5 cells at position 0 are shown solid.

Uniform polytopes with A₄ symmetry

#	Name	Coxeter diagram and Schläfli symbols	Coxeter plane graphs			Schlegel diagram		Net
			A4 [5]	A3 [4]	A2 [3]	Tetrahedron centered	Dual tetrahedron centered
1	5-cell pentachoron	{3,3,3}
2	rectified 5-cell	r{3,3,3}
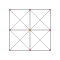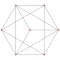3	truncated 5-cell	t{3,3,3}
4	cantellated 5-cell	rr{3,3,3}
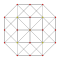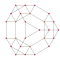
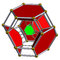
7	cantitruncated 5-cell	tr{3,3,3}
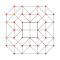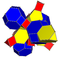8	runcitruncated 5-cell	t0,1,3{3,3,3}

Uniform polytopes with extended A₄ symmetry

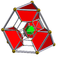#	Name	Coxeter diagram and Schläfli symbols	Coxeter plane graphs			Schlegel diagram	Net
			A4 [[5]] = [10]	A3 [4]	A2 [[3]] = [6]	Tetrahedron centered
5	*runcinated 5-cell	t0,3{3,3,3}
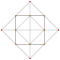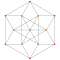6	*bitruncated 5-cell decachoron	2t{3,3,3}
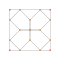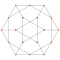9	*omnitruncated 5-cell	t0,1,2,3{3,3,3}

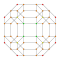Coordinates

The coordinates of uniform 4-polytopes with pentachoric symmetry can be generated as permutations of simple integers in 5-space, all in hyperplanes with normal vector (1,1,1,1,1). The A4 Coxeter group is palindromic, so repeated polytopes exist in pairs of dual configurations. There are 3 symmetric positions, and 6 pairs making the total 15 permutations of one or more rings. All 15 are listed here in order of binary arithmetic for clarity of the coordinate generation from the rings in each corresponding Coxeter diagram.

The number of vertices can be deduced here from the permutations of the number of coordinates, peaking at 5 factorial for the omnitruncated form with 5 unique coordinate values.

5-cell truncations in 5-space:

#	Base point	Name (symmetric name)	Coxeter diagram	Vertices
1	(0, 0, 0, 0, 1) (1, 1, 1, 1, 0)	5-cell Trirectified 5-cell		5	5!/(4!)
2	(0, 0, 0, 1, 1) (1, 1, 1, 0, 0)	Rectified 5-cell Birectified 5-cell		10	5!/(3!2!)
3	(0, 0, 0, 1, 2) (2, 2, 2, 1, 0)	Truncated 5-cell Tritruncated 5-cell		20	5!/(3!)
5	(0, 1, 1, 1, 2)	Runcinated 5-cell		20	5!/(3!)
4	(0, 0, 1, 1, 2) (2, 2, 1, 1, 0)	Cantellated 5-cell Bicantellated 5-cell		30	5!/(2!2!)
6	(0, 0, 1, 2, 2)	Bitruncated 5-cell		30	5!/(2!2!)
7	(0, 0, 1, 2, 3) (3, 3, 2, 1, 0)	Cantitruncated 5-cell Bicantitruncated 5-cell		60	5!/2!
8	(0, 1, 1, 2, 3) (3, 2, 2, 1, 0)	Runcitruncated 5-cell Runcicantellated 5-cell		60	5!/2!
9	(0, 1, 2, 3, 4)	Omnitruncated 5-cell		120	5!

References

J.H. Conway and M.J.T. Guy: Four-Dimensional Archimedean Polytopes, Proceedings of the Colloquium on Convexity at Copenhagen, page 38 und 39, 1965
John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 26)
H.S.M. Coxeter:
H.S.M. Coxeter, Regular Polytopes, 3rd Edition, Dover New York, 1973
Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 Wiley::Kaleidoscopes: Selected Writings of H.S.M. Coxeter
(Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
(Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591]
(Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. Dissertation, University of Toronto, 1966

External links

Klitzing, Richard. "4D uniform 4-polytopes".
Uniform, convex polytopes in four dimensions:, Marco Möller (in German)
Möller, Marco (2004). Vierdimensionale Archimedische Polytope (PDF) (Doctoral dissertation) (in German). University of Hamburg.
Uniform Polytopes in Four Dimensions, George Olshevsky.
Convex uniform polychora based on the pentachoron, George Olshevsky.

Fundamental convex regular and uniform polytopes in dimensions 2–10
Family	An	Bn	I2(p) / Dn	E6 / E7 / E8 / F4 / G2	Hn
Regular polygon	Triangle	Square	p-gon	Hexagon	Pentagon
Uniform polyhedron	Tetrahedron	Octahedron • Cube	Demicube		Dodecahedron • Icosahedron
Uniform 4-polytope	5-cell	16-cell • Tesseract	Demitesseract	24-cell	120-cell • 600-cell
Uniform 5-polytope	5-simplex	5-orthoplex • 5-cube	5-demicube
Uniform 6-polytope	6-simplex	6-orthoplex • 6-cube	6-demicube	122 • 221
Uniform 7-polytope	7-simplex	7-orthoplex • 7-cube	7-demicube	132 • 231 • 321
Uniform 8-polytope	8-simplex	8-orthoplex • 8-cube	8-demicube	142 • 241 • 421
Uniform 9-polytope	9-simplex	9-orthoplex • 9-cube	9-demicube
Uniform 10-polytope	10-simplex	10-orthoplex • 10-cube	10-demicube
Uniform n-polytope	n-simplex	n-orthoplex • n-cube	n-demicube	1k2 • 2k1 • k21	n-pentagonal polytope
Topics: Polytope families • Regular polytope • List of regular polytopes and compounds

Undergraduate Texts in Mathematics

Graduate Texts in Mathematics

Graduate Studies in Mathematics

Mathematics Encyclopedia

World

Index

Hellenica World - Scientific Library

Retrieved from "http://en.wikipedia.org/"
All text is available under the terms of the GNU Free Documentation License