.

The rectangle contained by the diagonals of any quadrilateral inscribed in a circle is equal to the sum of the rectangles contained by the pairs of opposite sides. Ptolemy, Almagest

Ptolemy's theorem refers to a quadrilateral inscribed in a circle. It is probably that actually Hipparchus discovered or knew much earlier Ptolemy's theorem (Tobias Dantzig even says it was a theorem of Apollonius). Unfortunately almost no work of Hipparchus survived and we know most about Hipparchus from Ptolemy's books and experts say that Ptolemy does not say always what was found originally by Hipparchus. Whatever the truth is the quadrilateral theorem today is known as Ptolemy's theorem. Ptolemy found that there is a constraint between the lengths of the sides and the diagonals of the quadrilateral. This is because only 3 points are necessary to define a circle and then some constraint is necessary for the additional points on the circle.

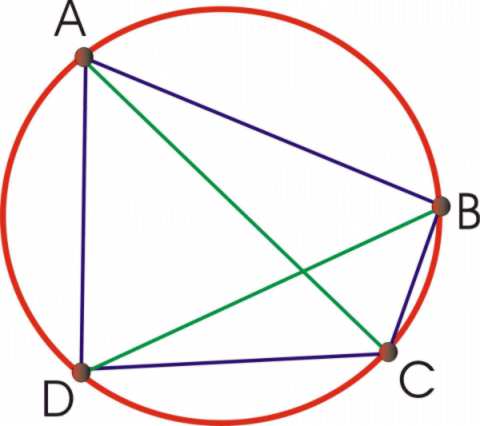
$Graphic1$

Ptolemy found that for the inscribed quadrilateral described by four points, A, B, C, D have to satisfy:

AC*BD = AB*CD + DA*BC

i.e. the product of the diagonals is the sum of the products of opposite sides.

If one quadrilateral diagonal is a diameter, then it subtends right angles at the circumference, so that the sides of the quadrilateral are the sines and cosines of the two acute angles of the right triangles, and the other diagonal is the sine of the sum of the acute angles. We obtain from this the sine addition theorem:

sin(α+β) = sin α cos β + cos α sin β.

The formula for the sine of the difference of two angles can be obtained in the same way by taking the other two vertices of the quadrilateral on the same side of the diameter, instead of on opposite sides.

For a rectangle we obtain the Pythagoras theorem. Ptolemy's theorem is not described in the Element's of Euclid but it was probably known before but it is described in Ptolemy's Almagest for the first time. Since Ptolemy generated tables of sines, although using another notation, he used probably this theorem as a version of the sine addition theorem to complete the sine tables.

The extension to the Ptolemy-Euler Theorem using complex numbers

The Ptolemy-Euler Theorem

For any four points A, B, C, D in the plane it follows:

|AB| |CD| + |BC| |DA| >= |AC| |BD|.

Equality holds if and only if these four points are cocyclic (colinear) and are in alphabetical order (clockwise or counterclockwise).

The equality discovered by Ptolemy was generalized over a thousand years later by L. Euler (1707-1783).

For any four complex numbers a, b, c, d, the following identity is true:

(a-b)(c-d) + (a-d)(b-c) = (a-c)(b-d)

Using the triangle inequality we obtain

|a-b||c-d| + |a-d||b-c| >= |a-c||b-d|

In case of the triangle inequality |z1 + z2| <= |z1| + |z2|,

equality holds if and only if z1/z2 is a positive real number (provided z1 z2 != 0).

Thus we are looking for a condition to ensure that (a-b)(c-d) : (a-d)(b-c) is a positive real number.

From Ptolemy to Pythagoras

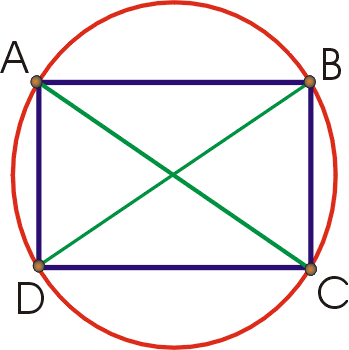
$Graphic3$

Take a rectangle with CD = AB, DA = BC , BD = AC

then from AC*BD = AB*CD + DA*BC follows if we set BD = AC, CD = AB and DA = BC:

AC² = AB² + BC²

^{See Ptolemy's Almagest}

Remarks:

Suppose C and D are on opposite sides of a line AB. Then the points A, B, C, D are cocyclic if and only if: angle(ACB) + angle(ADB) = PI.

(a-b)(c-d)/ (a-d)(b-c) is a positive real number

<=> ((a-b) / (a-d))((a-d) /(c-d)) is a negative real number

<=> arg( (a-b)/(a-d)) /( (c-b)/(c-d) ) = PI

<=> arg( (a-b)/(a-d)) -arg( (c-b)/(c-d) ) = PI (mod 2 PI)

It follows that a, b, c, d are cocyclic, i.e. a, b, c, d are on the same circle or line and a and c are on the opposite sides of the chord joining b and d, which results in the alphabetical order (clockwise or counterclockwise).

Interpolation

Ptolemy calculated in principle trigonometric tables even if he did not use trigonometric functions used today. He used an interpolation method to produce these tables. In order to avoid complicated calculations for the functions of more than one variable, Ptolemy used an approach that amounts to tabulating the function only for the variable for which the function varies most, given two bounding values of the other variable, and to provide a table of coefficients to be used in an adaptive linear interpolation scheme for computation of the function for intermediate values of this latter variable.

Erik Meijering, A Chronology of Interpolation, From Ancient Astronomy to Modern Signal and Image Processing, Proceedings of the IEEE, vol. 90, no. 3, March 2002, pp. 319{342

G. van Brummelen, Lunar and Planetary Interpolation Tables in Ptolemy's Almagest, Journal for the History of Astronomy, vol. 25, no. 4, 1994, pp. 297-311.

Tobias Dantzig, The Bequest of the Greeks (New York: Charles Scribner’s Sons, 1955)

Ptolemy the Geographer and his Maps

Example 1 from Almagest i 10, H43-45
Example 2 from Almagest xii 1, Trigonometric Lemma of Apollonius (xii 1)

On Ptolemy's Theorem

Ancient Greece

Science, Technology , Medicine , Warfare, , Biographies , Life , Cities/Places/Maps , Arts , Literature , Philosophy ,Olympics, Mythology , History , Images