.

Griechische Mathematik: Pappos von Alexandria

Bees were endowed with a certain geometrical forethought .... There being, then, three figures which of themselves can fill up the space round a point, viz. the triangle, the square and the hexagon, the bees have wisely selected for their structure that which contains the most angles, suspecting indeed that it could hold more honey than either of the other two. Pappus of Aelxandria

Pappus (or Pappos) of Alexandria (Πάππος ο Αλεξανδρεύς) (about 290-350) AD is the author of Μαθηματική Συναγωγή, or shortly Συναγωγή (Synagoge) (Mathematical Collections), which contained as the name suggests a collection of all the Mathematics known until Pappus' time. Very little is known about his life and the only date that is very accurate is the solar eclipse which he observed on 18^th October 320 AD.

Commandinus provided the first translation into Latin 1589. Others like Wallis followed until 1878 when Friedrich Hultsch provided a complete translation.

The Mathematical Collections of Pappus in a translation of Federico Commandino (1589).

An Image from a Vatican Exhibition

Although there is little originality, Pappus showed great understanding in all topics.

Book I and II covered Arithmetics . Both books excepts parts of II are lost. Book II considered very large numbers.

Book III contained a range of topics: mean proportional; arithmetic, geometric and harmonic means (10 different types of mean in summary); some geometrical paradoxes; inscription of the 5 Regular Polyhedra in a Sphere. Pappus considers so-called linear problems (solvable with straight edge and compass ), solid problems (requiring solution of some cubic equations) and linear problems (using higher order curves, spirals, quadratices, etc)

Book IV treated curves such as spirals and the quadratrix (two construction methods described: using a cylindrical helix, and using a right cylinder the base of which is an Archimedian spiral).

Book V reviewed the plane tessellation problem (Honeycomb, hexagonal cells). Pappus discusses the honeycomb conjecture: Any partition of the plane into regions of equal area has perimeter at least that of the regular hexagonal grid. The conjecture was finally proved by Hales (1999, 2001). Pappus refers to the problem and other optimization problems in his fifth book. See: Optimization Problems ; and the results of Zenodorus (isoperimetry problems). Pappus also considers the 13 semi-regular solids of Archimedes;

Book VI is on Astronomy discussing the work or Aristarchus, Autolycus of Pithane, Theodosius of Bithynia and others (considers optics: reflection and refraction.)

Book VII discussed the later known as Pappus-Guldin Theorem, conic sections,

Analysis and synthesis:

Now, analysis is the path from what one is seeking, as if it were established, by way of its consequences, to something that is established by synthesis. That is to say, in analysis we assume what is sought as if it has been achieved, and look for the thing from which it follows, and again what comes before that, until by regressing in this way we come upon some one of the things that are already known, or that occupy the rank of a first principle. We call this kind of method “analysis” as if to say anapalin lysis (reduction backward). In synthesis, by reversal we assume what was obtained last in the analysis to have been achieved already, and, setting now in natural order, as precedents, what before were following, and fitting them to each other, we attain the end of the construction of what was sought. This is what we call “synthesis.

'Pappus Problem' (now known as Pappus' Hexagon Theorem).

Book VIII is on Mechanics and described the so-called Pappus-Pascal Theorem. See Pappus Alexandrinus Mathematical Collection, Book 8

Pappus's Hexagonal Theorem

If ABC and A'B'C' are straigth lines; and A'', B'', C'' are the intersections of AB' with A'B, AC' with A'C, BC' with B'C respectively: then A''B''C'' is a straight line.

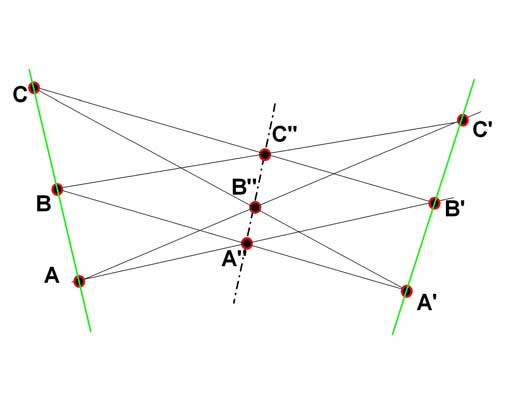
$Grafik2$

What Pappus did not know is what happens if we continue the process with the new line A''B''C'' and the original lines ABC and A'B'C' :

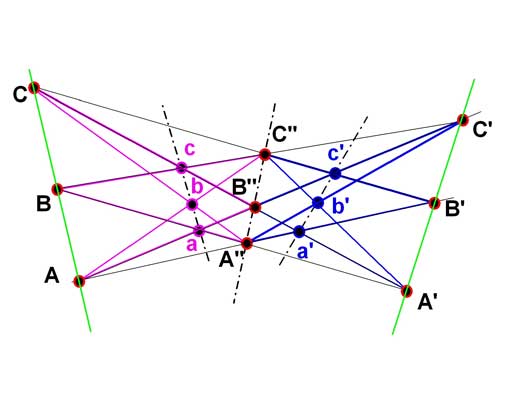
$Grafik3$

In a new iteration we obtain two new lines abc and a'b'c' and we can continue this process further. An example from an article written by Marcel Berger is shown after 5 iterations. If the process continues the result is a fractal structure with interesting mathematical properties. See: Richard Evan Schwartz, Pappus's theorem and the modular group. Publications Mathématiques de l'IHÉS, 78 (1993), p. 187-206 (PDF File)

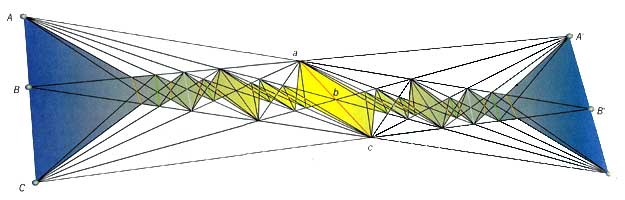
$Grafik4$

Marcel Berger, Das Unendliche in der Geometrie (The Infinite in Geometry), Spektrum Spezial: Das Unendliche, p. 38, ND 1/2003.

An Introduction to Pappus' Theorem with a Java Applet

A proof and more information about Pappus's Theorem

Pappus's Centroid Theorem

Volume of revolution = (area bounded by the curve) * (distance traveled by the center of gravity)

Eric W. Weisstein. "Pappus's Centroid Theorem." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/PappussCentroidTheorem.html

Pappus-Guldin (or Guldinus) Theorem (Paul (Habakkuk) Guldin (12.6.1577-3.11.1643) provided around 1640 the proof)

Pappus' Area Theorem A generalization of the Pythagoras Theorem (extended Theorem).

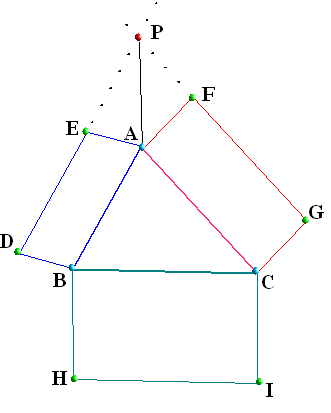
$Grafik1$

Take a triangle ABC, generate on the two sides two parallelograms DEAB and AFGC. Extend ED and FG. They intersect at the point P.

Construct a parallelogram BHIC using the triangle side BC and BH = CI = PA

Then for the areas of the parallelograms DEAB, AFGC, BHIC we have: DEAB + AFGC = BHIC

See: A proof of the Pappus' Area Theorem

Pythagoras Theorem: A proof suggested by Pappus' Theorem

Other lost books

Comments on Aristarchus' On magnitudes , Comments on Euclid's Data and on Euclid's Elements (partly known from an Arabic translation), Comments on the Analemma of Diodorus of Alexandria, Commentary on Ptolemy's Syntaxis

For more information about the work of Pappus see:

http://www.math.tamu.edu/~don.allen/history/pappus/pappus.html

LINKS

Eric W. Weisstein. "Pappus Chain." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/PappusChain.html

From Vignettes of Ancient Mathematics by Henry Mendell, Cal. State U., L.A.

Theorems on the Archimedes spiral (Book 1V §§21-25):
Theorems on the Archimedes spiral (Book 1V §§21-25)
Theorems and claims on Nicomedes' 1st cochloid (§§26-29):
Quadratrix (Book 1V §§30-34)
Division of angle by a given ratio (Book IV §§45-47):
Four propositions, three explicitly using quadratices (Book IV §§48-51):
Four lemmas for isoperimetric theorems (Book V §§11-14, pp. 234.22-242.12):
Introductory lemmas on spherics and theorems relating to Theodosius, Sphaerica, iii 5 (Book VI §§1-11, pp. 474.1-488.25):