"... we have a collection of Lemmas which has reached us through the Arabic. [...] The Lemmas cannot, however, have been written by Archimedes in their present form, because his name is quoted in them more than once. ...though it is quite likely that some of the propositions were of Archimedean origin, e.g. those concerning the geometrical figures called respectively arbelos [in Greek, jgc] (literally 'shoemaker's knife') and salinon [in Greek, jgc] (probably a'salt-cellar'), ..." Thomas L. Heath, The Works of Archimedes

Archimedes of Syracuse (Αρχιμήδης ο Συρακούσιος)(287-212 BC) himself is believed to have been the first mathematician to study the mathematical properties of the “Arbelos”. The term arbelos means shoemaker's knife in Greek, and this term is applied to the shaded area in the above figure which resembles the blade of a knife used by ancient cobblers.

The Greek word: o (a)/rbhlos [the arbelos; of masc. gender] means the knife of the shoemaker (h is used for the symbol eta) . From the same stem arb- we have also: h (a)rbu/lh [of fem. Gender] : a kind of shoes (half-boot; like soldier's half-boot). This word survives in modern Greek but in its Doric form, that is, with the ending alpha (a) instead of eta (h) : h (a)rbu/la Antreas P. Hatzipolakis

A shoemaker with an arbelos cutting leather for shoes (The Cambridge illustrated history of ancient Greece, edited by Paul Cartledge, Cambridge University Press, 1998.)

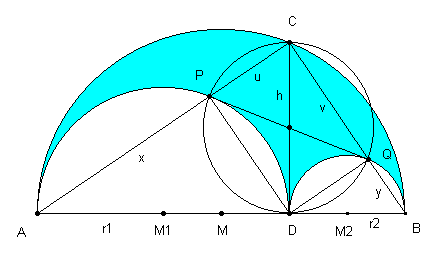
The arbelos is the blue shaded area below two circles with diameter AD and (AB-AD). The position of the central notch D is arbitrary and can be located anywhere along the diameter AB.

The arc length along the enclosing semicircle AB is the same as the arc length along the two smaller semicircles AD and DB.

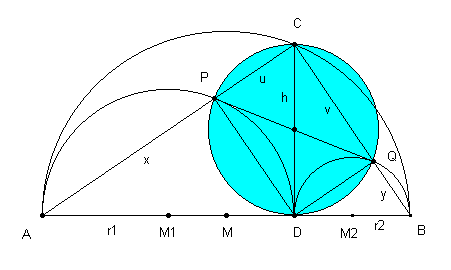
If we take the perpendicular at D that intersects the circle at C then there is an associated blue circle shown below that has the same area as the arbelos.

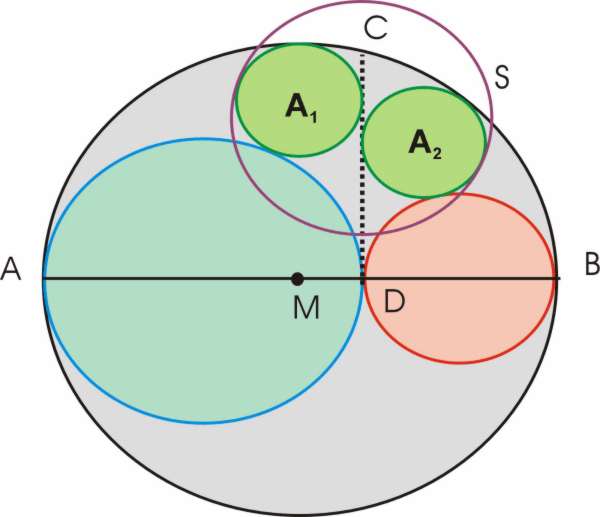
The circles A₁ and A₂ inscribed in the two parts of the arbelos ADC and CDB are called Archimedian twin circles and their area is the same. The smallest circle S that encloses A₁ and A₂ has the same area as the arbelos.

The Twin Circles of Archimedes (Java Applet) (German Site)

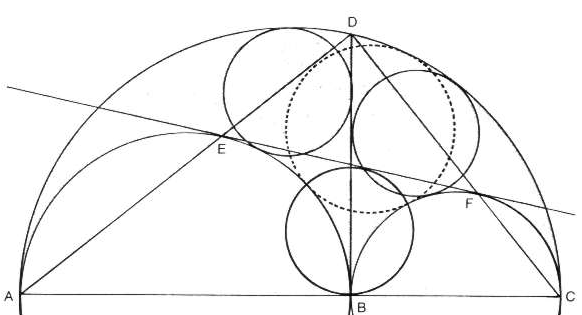
If we take the tangent through the two semicircles at E and F then EF and BD are of the same length since they are they are the diagonals of a circle having as center the intersection point of EF and BD.

Archimedes' Twin Circles and a Brother (Java Applet)

EF = BD

From the point B and EF a circle can be constructed that has the same area as the two Archimedian “twin” circles. So actually there are not only 2 but 3 Archimedian circles.

Arbelos: The shoemaker's knife

The Salinon

http://mathcentral.uregina.ca/QQ/database/QQ.09.98/craig1.html

Salinon Proof without words (PDF File)

LINKS

Essay # 4 - The Arbelos and the Salinon

A Dozen More Arbelos Twins

Arbelos Proofs (Cut the knot site)

Archimedes and the Arbelos

Inversive Geometry and the Arbelos

http://www.retas.de/thomas/arbelos/arbelos.html Thomas Schoch, Amazing Properties of the Arbelos (Applet)

References

See an applet: Allanson, B. "Pappus's Arbelos" http://members.ozemail.com.au/~llan/arbelos.html.
L. Bankoff, Are the twin circles of Archimedes really twins?, Math. Mag., 47 (1974) 214–-218.
L. Bankoff, The marvelous arbelos, in The lighter side of mathematics 247-253, ed. R. K. Guy and R. E. Woodrow, Mathematical Association of America, 1994.
Peter Y. Woo Simple Constructions of the Incircle of an Arbelos, Forum Geometricorum, Volume 1 (2001) 133–-136. PDF (50KB)

Eric W. Weisstein:

"Salinon." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/Salinon.html
"Pappus Chain." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/PappusChain.html
Martin Gardner, Scientific American, Jan. 1979, p.118
Hiroshi Okumura and Masayuki Watanabe, The Archimedean Circles of Schoch and Woo, Forum Geometricorum, Volume 4 (2004) 27–34. Abstract
Hiroshi Okumura and Masayuki Watanabe, The Twin Circles of Archimedes in a Skewed Arbelos, Forum Geometricorum Volume 4 (2004) 229-–251. Abstract

Miscellaneous

Arc Figures: Figures formed by (circular) arcs

shoemaker's cubics

Concyclic Points in Arbelos , Rectangle in Arbelos

Pappus and the Arbelos